radiation, being used routinely in medical and dental x rays. Nuclear radiation is also captured on film, such as seen in Figure 31.8. The mechanism for film exposure by ionizing radiation is similar to that by photons. A quantum of energy interacts with the emulsion and alters it chemically, thus
exposing the film. The quantum come from an α -particle, β -particle, or photon, provided it has more than the few eV of energy needed to induce
the chemical change (as does all ionizing radiation). The process is not 100% efficient, since not all incident radiation interacts and not all interactions
produce the chemical change. The amount of film darkening is related to exposure, but the darkening also depends on the type of radiation, so that
absorbers and other devices must be used to obtain energy, charge, and particle-identification information.

1116 CHAPTER 31 | RADIOACTIVITY AND NUCLEAR PHYSICS
Figure 31.8 Film badges contain film similar to that used in this dental x-ray film and is sandwiched between various absorbers to determine the penetrating ability of the
radiation as well as the amount. (credit: Werneuchen, Wikimedia Commons)
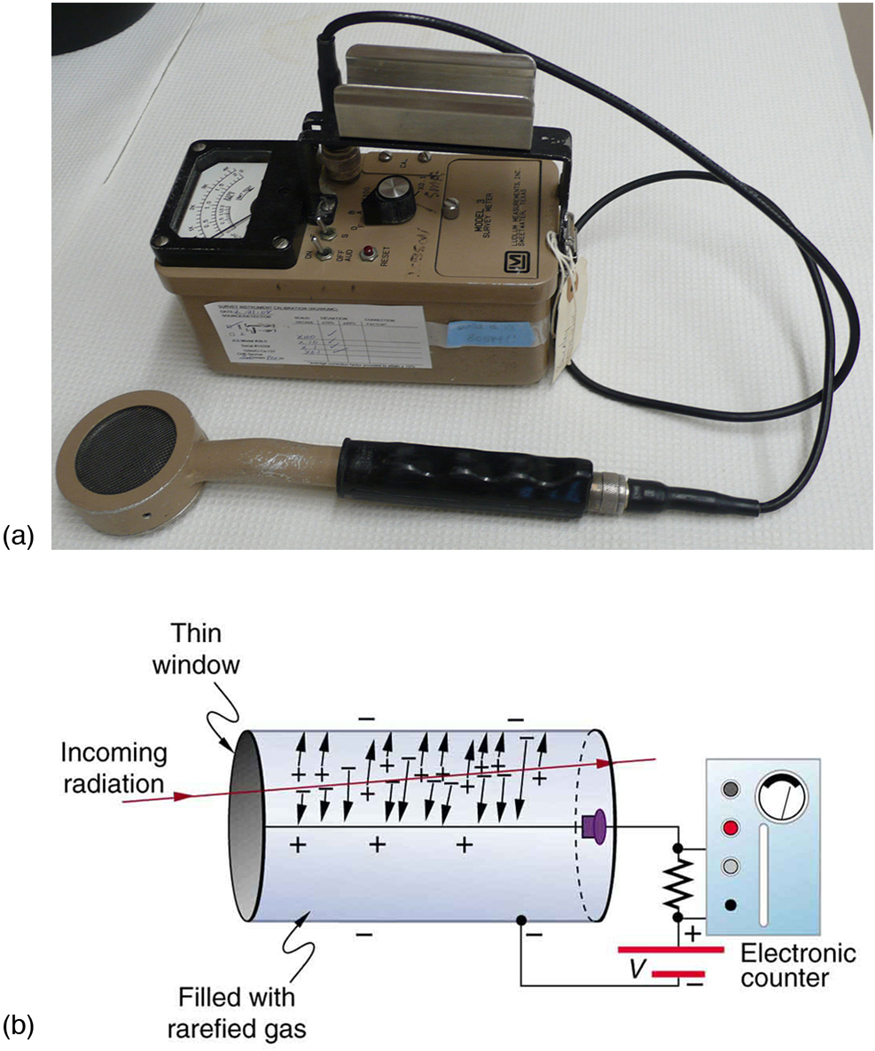
Another very common radiation detector is the Geiger tube. The clicking and buzzing sound we hear in dramatizations and documentaries, as well
as in our own physics labs, is usually an audio output of events detected by a Geiger counter. These relatively inexpensive radiation detectors are
based on the simple and sturdy Geiger tube, shown schematically in Figure 31.9(b). A conducting cylinder with a wire along its axis is filled with an insulating gas so that a voltage applied between the cylinder and wire produces almost no current. Ionizing radiation passing through the tube
produces free ion pairs that are attracted to the wire and cylinder, forming a current that is detected as a count. The word count implies that there is
no information on energy, charge, or type of radiation with a simple Geiger counter. They do not detect every particle, since some radiation can pass
through without producing enough ionization to be detected. However, Geiger counters are very useful in producing a prompt output that reveals the
existence and relative intensity of ionizing radiation.
Figure 31.9 (a) Geiger counters such as this one are used for prompt monitoring of radiation levels, generally giving only relative intensity and not identifying the type or
energy of the radiation. (credit: TimVickers, Wikimedia Commons) (b) Voltage applied between the cylinder and wire in a Geiger tube causes ions and electrons produced by
radiation passing through the gas-filled cylinder to move towards them. The resulting current is detected and registered as a count.
Another radiation detection method records light produced when radiation interacts with materials. The energy of the radiation is sufficient to excite
atoms in a material that may fluoresce, such as the phosphor used by Rutherford’s group. Materials called scintillators use a more complex
collaborative process to convert radiation energy into light. Scintillators may be liquid or solid, and they can be very efficient. Their light output can
provide information about the energy, charge, and type of radiation. Scintillator light flashes are very brief in duration, enabling the detection of a huge
number of particles in short periods of time. Scintillator detectors are used in a variety of research and diagnostic applications. Among these are the
detection by satellite-mounted equipment of the radiation from distant galaxies, the analysis of radiation from a person indicating body burdens, and
the detection of exotic particles in accelerator laboratories.

CHAPTER 31 | RADIOACTIVITY AND NUCLEAR PHYSICS 1117
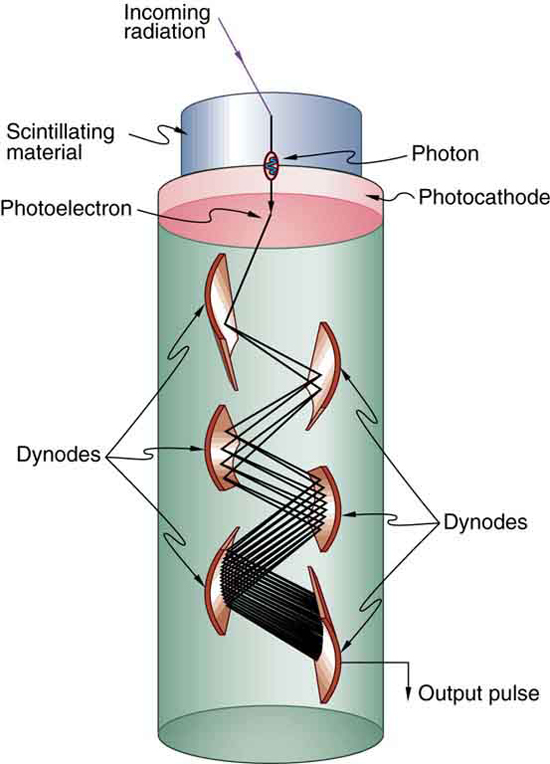
Light from a scintillator is converted into electrical signals by devices such as the photomultiplier tube shown schematically in Figure 31.10. These
tubes are based on the photoelectric effect, which is multiplied in stages into a cascade of electrons, hence the name photomultiplier. Light entering
the photomultiplier strikes a metal plate, ejecting an electron that is attracted by a positive potential difference to the next plate, giving it enough
energy to eject two or more electrons, and so on. The final output current can be made proportional to the energy of the light entering the tube, which
is in turn proportional to the energy deposited in the scintillator. Very sophisticated information can be obtained with scintillators, including energy,
charge, particle identification, direction of motion, and so on.
Figure 31.10 Photomultipliers use the photoelectric effect on the photocathode to convert the light output of a scintillator into an electrical signal. Each successive dynode has a more-positive potential than the last and attracts the ejected electrons, giving them more energy. The number of electrons is thus multiplied at each dynode, resulting in an
easily detected output current.
Solid-state radiation detectors convert ionization produced in a semiconductor (like those found in computer chips) directly into an electrical signal.
Semiconductors can be constructed that do not conduct current in one particular direction. When a voltage is applied in that direction, current flows
only when ionization is produced by radiation, similar to what happens in a Geiger tube. Further, the amount of current in a solid-state detector is
closely related to the energy deposited and, since the detector is solid, it can have a high efficiency (since ionizing radiation is stopped in a shorter
distance in solids fewer particles escape detection). As with scintillators, very sophisticated information can be obtained from solid-state detectors.
PhET Explorations: Radioactive Dating Game
Learn about different types of radiometric dating, such as carbon dating. Understand how decay and half life work to enable radiometric dating to
work. Play a game that tests your ability to match the percentage of the dating element that remains to the age of the object.
Figure 31.11 Radioactive Dating Game (http://cnx.org/content/m42627/1.4/radioactive-dating-game_en.jar)
31.3 Substructure of the Nucleus
What is inside the nucleus? Why are some nuclei stable while others decay? (See Figure 31.12.) Why are there different types of decay ( α , β and γ )? Why are nuclear decay energies so large? Pursuing natural questions like these has led to far more fundamental discoveries than you might
imagine.

1118 CHAPTER 31 | RADIOACTIVITY AND NUCLEAR PHYSICS
Figure 31.12 Why is most of the carbon in this coal stable (a), while the uranium in the disk (b) slowly decays over billions of years? Why is cesium in this ampule (c) even less stable than the uranium, decaying in far less than 1/1,000,000 the time? What is the reason uranium and cesium undergo different types of decay ( α and β , respectively)?
(credits: (a) Bresson Thomas, Wikimedia Commons; (b) U.S. Department of Energy; (c) Tomihahndorf, Wikimedia Commons)
We have already identified protons as the particles that carry positive charge in the nuclei. However, there are actually two types of particles in the
nuclei—the proton and the neutron, referred to collectively as nucleons, the constituents of nuclei. As its name implies, the neutron is a neutral
particle ( q = 0 ) that has nearly the same mass and intrinsic spin as the proton. Table 31.2 compares the masses of protons, neutrons, and electrons. Note how close the proton and neutron masses are, but the neutron is slightly more massive once you look past the third digit. Both
nucleons are much more massive than an electron. In fact, m p = 1836 me (as noted in Medical Applications of Nuclear Physics and
mn = 1839 me .
Table 31.2 also gives masses in terms of mass units that are more convenient than kilograms on the atomic and nuclear scale. The first of these is the unified atomic mass unit (u), defined as
(31.1)
1 u = 1.6605×10−27 kg.
This unit is defined so that a neutral carbon 12 C atom has a mass of exactly 12 u. Masses are also expressed in units of MeV/ c 2 . These units are
very convenient when considering the conversion of mass into energy (and vice versa), as is so prominent in nuclear processes. Using E = mc 2
and units of m in MeV/ c 2 , we find that c 2 cancels and E comes out conveniently in MeV. For example, if the rest mass of a proton is converted
entirely into energy, then
(31.2)
E = mc 2 = (938.27 MeV/ c 2) c 2 = 938.27 MeV.
It is useful to note that 1 u of mass converted to energy produces 931.5 MeV, or
(31.3)
1 u = 931.5 MeV/ c 2.
All properties of a nucleus are determined by the number of protons and neutrons it has. A specific combination of protons and neutrons is called a
nuclide and is a unique nucleus. The following notation is used to represent a particular nuclide:
A
(31.4)
Z X N,
where the symbols A , X , Z , and N are defined as follows: The number of protons in a nucleus is the atomic number Z , as defined in Medical
Applications of Nuclear Physics. X is the symbol for the element, such as Ca for calcium. However, once Z is known, the element is known; hence, Z and X are redundant. For example, Z = 20 is always calcium, and calcium always has Z = 20 . N is the number of neutrons in a
nucleus. In the notation for a nuclide, the subscript N is usually omitted. The symbol A is defined as the number of nucleons or the total number of
protons and neutrons,
A
(31.5)
= N + Z,
where A is also called the mass number. This name for A is logical; the mass of an atom is nearly equal to the mass of its nucleus, since
electrons have so little mass. The mass of the nucleus turns out to be nearly equal to the sum of the masses of the protons and neutrons in it, which
is proportional to A . In this context, it is particularly convenient to express masses in units of u. Both protons and neutrons have masses close to 1
u, and so the mass of an atom is close to A u. For example, in an oxygen nucleus with eight protons and eight neutrons, A = 16 , and its mass is
16 u. As noticed, the unified atomic mass unit is defined so that a neutral carbon atom (actually a 12 C atom) has a mass of exactly 12 u . Carbon
was chosen as the standard, partly because of its importance in organic chemistry (see Appendix A).
Table 31.2 Masses of the Proton, Neutron, and Electron
Particle
Symbol
kg
u
MeV c2
Proton
p
1.67262×10−27 1.007276 938.27
Neutron
n
1.67493 × 10−27 1.008665 939.57
Electron
e
9.1094 × 10−31 0.00054858 0.511
Let us look at a few examples of nuclides expressed in the A
1
Z X N notation. The nucleus of the simplest atom, hydrogen, is a single proton, or 1 H
(the zero for no neutrons is often omitted). To check this symbol, refer to the periodic table—you see that the atomic number Z of hydrogen is 1.

CHAPTER 31 | RADIOACTIVITY AND NUCLEAR PHYSICS 1119
Since you are given that there are no neutrons, the mass number A is also 1. Suppose you are told that the helium nucleus or α particle has two
protons and two neutrons. You can then see that it is written 42 He2 . There is a scarce form of hydrogen found in nature called deuterium; its nucleus
has one proton and one neutron and, hence, twice the mass of common hydrogen. The symbol for deuterium is, thus, 21 H1 (sometimes D is used,
as for deuterated water D2 O ). An even rarer—and radioactive—form of hydrogen is called tritium, since it has a single proton and two neutrons,
and it is written 31 H2 . These three varieties of hydrogen have nearly identical chemistries, but the nuclei differ greatly in mass, stability, and other
characteristics. Nuclei (such as those of hydrogen) having the same Z and different N s are defined to be isotopes of the same element.
There is some redundancy in the symbols A , X , Z , and N . If the element X is known, then Z can be found in a periodic table and is always
the same for a given element. If both A and X are known, then N can also be determined (first find Z ; then, N = A − Z ). Thus the simpler notation for nuclides is
A
(31.6)
X,
which is sufficient and is most commonly used. For example, in this simpler notation, the three isotopes of hydrogen are 1 H, 2 H, and 3 H, while
the α particle is 4 He . We read this backward, saying helium-4 for 4 He , or uranium-238 for 238 U . So for 238 U , should we need to know, we
can determine that Z = 92 for uranium from the periodic table, and, thus, N = 238 − 92 = 146 .
A variety of experiments indicate that a nucleus behaves something like a tightly packed ball of nucleons, as illustrated in Figure 31.13. These
nucleons have large kinetic energies and, thus, move rapidly in very close contact. Nucleons can be separated by a large force, such as in a collision
with another nucleus, but resist strongly being pushed closer together. The most compelling evidence that nucleons are closely packed in a nucleus
is that the radius of a nucleus, r , is found to be given approximately by
(31.7)
r = r 0 A 1/3,
where r 0 = 1.2 fm and A is the mass number of the nucleus. Note that r 3 ∝ A . Since many nuclei are spherical, and the volume of a sphere is
V = (4 / 3) πr 3 , we see that V ∝ A —that is, the volume of a nucleus is proportional to the number of nucleons in it. This is what would happen if
you pack nucleons so closely that there is no empty space between them.
Figure 31.13 A model of the nucleus.
Nucleons are held together by nuclear forces and resist both being pulled apart and pushed inside one another. The volume of the nucleus is the sum
of the volumes of the nucleons in it, here shown in different colors to represent protons and neutrons.
Example 31.1 How Small and Dense Is a Nucleus?
(a) Find the radius of an iron-56 nucleus. (b) Find its approximate density in kg / m3 , approximating the mass of 56Fe to be 56 u.
Strategy and Concept
(a) Finding the radius of 56 Fe is a straightforward application of r = r 0 A 1 / 3, given A = 56 . (b) To find the approximate density, we assume
the nucleus is spherical (this one actually is), calculate its volume using the radius found in part (a), and then find its density from ρ = m/V .
Finally, we will need to convert density from units of u / fm3 to kg/ m3 .
Solution
(a) The radius of a nucleus is given by
(31.8)
r = r 0 A 1/3.
Substituting the values for r 0 and A yields
(31.9)
r = (1.2 fm)(56)1/3 = (1.2 fm)(3.83)
= 4.6 fm.
(b) Density is defined to be ρ = m/V , which for a sphere of radius r is
(31.10)
ρ = mV = m
(4/3) πr 3.
1120 CHAPTER 31 | RADIOACTIVITY AND NUCLEAR PHYSICS
Substituting known values gives
(31.11)
ρ =
56 u
(1.33)(3.14)(4.6 fm)3
= 0.138 u/fm3.
Converting to units of kg / m3 , we find
(31.12)
ρ = (0.138 u/fm3)(1.66×10–27 kg/u)⎛ 1 fm ⎞
⎝10–15 m⎠
= 2.3×1017 kg/m3.
Discussion
(a) The radius of this medium-sized nucleus is found to be approximately 4.6 fm, and so its diameter is about 10 fm, or 10–14 m . In our
discussion of Rutherford’s discovery of the nucleus, we noticed that it is about 10–15 m in diameter (which is for lighter nuclei), consistent with
this result to an order of magnitude. The nucleus is much smaller in diameter than the typical atom, which has a diameter of the order of
10–10 m .
(b) The density found here is so large as to cause disbelief. It is consistent with earlier discussions we have had about the nucleus being very
small and containing nearly all of the mass of the atom. Nuclear densities, such as found here, are about 2×1014 times greater than that of
water, which has a density of “only” 103 kg/m3 . One cubic meter of nuclear matter, such as found in a neutron star, has the same mass as a
cube of water 61 km on a side.
Nuclear Forces and Stability
What forces hold a nucleus together? The nucleus is very small and its protons, being positive, exert tremendous repulsive forces on one another.
(The Coulomb force increases as charges get closer, since it is proportional to 1 / r 2 , even at the tiny distances found in nuclei.) The answer is that
two previously unknown forces hold the nucleus together and make it into a tightly packed ball of nucleons. These forces are called the weak and
strong nuclear forces. Nuclear forces are so short ranged that they fall to zero strength when nucleons are separated by only a few fm. However, like
glue, they are strongly attracted when the nucleons get close to one another. The strong nuclear force is about 100 times more attractive than the
repulsive EM force, easily holding the nucleons together. Nuclear forces become extremely repulsive if the nucleons get too close, making nucleons
strongly resist being pushed inside one another, something like ball bearings.
The fact that nuclear forces are very strong is responsible for the very large energies emitted in nuclear decay. During decay, the forces do work, and
since work is force times the distance ( W = Fd cos θ ), a large force can result in a large emitted energy. In fact, we know that there are two distinct nuclear forces because of the different types of nuclear decay—the strong nuclear force is responsible for α decay, while the weak nuclear force is
responsible for β decay.
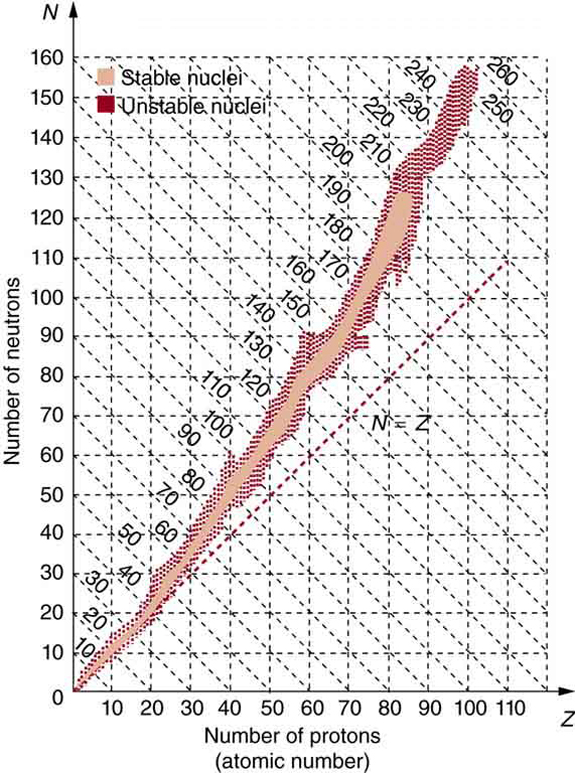
The many stable and unstable nuclei we have explored, and the hundreds we have not discussed, can be arranged in a table called the chart of the
nuclides, a simplified version of which is shown in Figure 31.14. Nuclides are located on a plot of N versus Z . Examination of a detailed chart of the nuclides reveals patterns in the characteristics of nuclei, such as stability, abundance, and types of decay, analogous to but more complex than
the systematics in the periodic table of the elements.

CHAPTER 31 | RADIOACTIVITY AND NUCLEAR PHYSICS 1121
Figure 31.14 Simplified chart of the nuclides, a graph of N versus Z for known nuclides. The patterns of stable and unstable nuclides reveal characteristics of the nuclear forces. The dashed line is for N = Z . Numbers along diagonals are mass numbers A .
In principle, a nucleus can have any combination of protons and neutrons, but Figure 31.14 shows a definite pattern for those that are stable. For low-mass nuclei, there is a strong tendency for N and Z to be nearly equal. This means that the nuclear force is more attractive when N = Z .
More detailed examination reveals greater stability when N and Z are even numbers—nuclear forces are more attractive when neutrons and
protons are in pairs. For increasingly higher masses, there are progressively more neutrons than protons in stable nuclei. This is due to the ever-
growing repulsion between protons. Since nuclear forces are short ranged, and the Coulomb force is long ranged, an excess of neutrons keeps the
protons a little farther apart, reducing Coulomb repulsion. Decay modes of nuclides out of the region of stability consistently produce nuclides closer
to the region of stability. There are more stable nuclei having certain numbers of protons and neutrons, called magic numbers. Magic numbers
indicate a shell structure for the nucleus in which closed shells are more stable. Nuclear shell theory has been very successful in explaining nuclear
energy levels, nuclear decay, and the greater stability of nuclei with closed shells. We have been producing ever-heavier transuranic elements since
the early 1940s, and we have now produced the element with Z = 118 . There are theoretical predictions of an island of relative stability for nuclei
with such high Z s.
Figure 31.15 The German-born American physicist Maria Goeppert Mayer (1906–1972) shared the 1963 Nobel Prize in physics with J. Jensen for the creation of the nuclear
shell model. This successful nuclear model has nucleons filling shells analogous to electron shells in atoms. It was inspired by patterns observed in nuclear properties. (credit:
Nobel Foundation via Wikimedia Commons)
31.4 Nuclear Decay and Conservation Laws
Nuclear decay has provided an amazing window into the realm of the very small. Nuclear decay gave the first indication of the connection between
mass and energy, and it revealed the existence of two of the four basic forces in nature. In this section, we explore the major modes of nuclear decay;
and, like those who first explored them, we will discover evidence of previously unknown particles and conservation laws.
1122 CHAPTER 31 | RADIOACTIVITY AND NUCLEAR PHYSICS
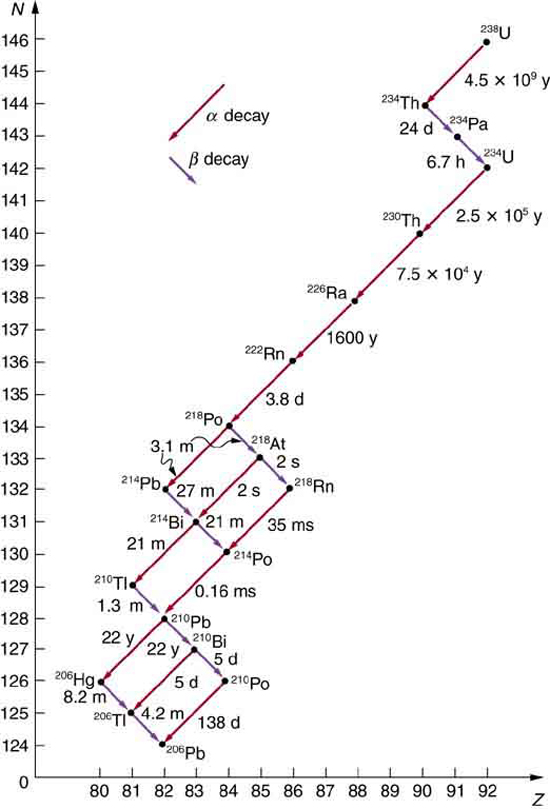
Some nuclides are stable, apparently living forever. Unstable nuclides decay (that is, they are radioactive), eventually producing a stable nuclide after
many decays. We call the original nuclide the parent and its decay products the daughters. Some radioactive nuclides decay in a single step to a
stable nucleus. For example, 60 Co is unstable and decays directly to 60 Ni , which is stable. Others, such as 238 U , decay to another unstable
nuclide, resulting in a decay series in which each subsequent nuclide decays until a stable nuclide is finally produced. The decay series that starts
from 238 U is of particular interest, since it produces the radioactive isotopes 226 Ra and 210 Po , which the Curies first discovered (see Figure












