2 s 2
B
5
"
2 s 2 2 p 1
C
6
"
2 s 2 2 p 2
N
7
"
2 s 2 2 p 3
O
8
"
2 s 2 2 p 4
F
9
"
2 s 2 2 p 5
Ne
10
"
2 s 2 2 p 6
Na
11
"
2 s 2 2 p 6 3 s 1
Mg
12
"
"
"
3 s 2
Al
13
"
"
"
3 s 2 3 p 1
Si
14
"
"
"
3 s 2 3 p 2
P
15
"
"
"
3 s 2 3 p 3
S
16
"
"
"
3 s 2 3 p 4
Cl
17
"
"
"
3 s 2 3 p 5
Ar
18
"
"
"
3 s 2 3 p 6
K
19
"
"
"
3 s 2 3 p 6 4 s 1
Ca
20
"
"
"
"
"
4 s 2
Examining the above table, you can see that as the number of electrons in an atom increases from 1 in hydrogen to 2 in helium and so on, the
lowest-energy shell gets filled first—that is, the n = 1 shell fills first, and then the n = 2 shell begins to fill. Within a shell, the subshells fill starting
with the lowest l , or with the s subshell, then the p , and so on, usually until all subshells are filled. The first exception to this occurs for potassium,
where the 4 s subshell begins to fill before any electrons go into the 3 d subshell. The next exception is not shown in Table 30.3; it occurs for
rubidium, where the 5 s subshell starts to fill before the 4 d subshell. The reason for these exceptions is that l = 0 electrons have probability
clouds that penetrate closer to the nucleus and, thus, are more tightly bound (lower in energy).
Figure 30.62 shows the periodic table of the elements, through element 118. Of special interest are elements in the main groups, namely, those in
the columns numbered 1, 2, 13, 14, 15, 16, 17, and 18.
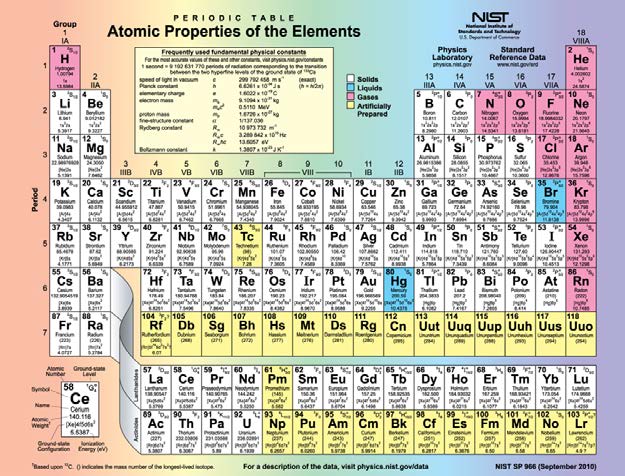

CHAPTER 30 | ATOMIC PHYSICS 1101
Figure 30.62 Periodic table of the elements (credit: National Institute of Standards and Technology, U.S. Department of Commerce)
The number of electrons in the outermost subshell determines the atom’s chemical properties, since it is these electrons that are farthest from the
nucleus and thus interact most with other atoms. If the outermost subshell can accept or give up an electron easily, then the atom will be highly
reactive chemically. Each group in the periodic table is characterized by its outermost electron configuration. Perhaps the most familiar is Group 18
(Group VIII), the noble gases (helium, neon, argon, etc.). These gases are all characterized by a filled outer subshell that is particularly stable. This
means that they have large ionization energies and do not readily give up an electron. Furthermore, if they were to accept an extra electron, it would
be in a significantly higher level and thus loosely bound. Chemical reactions often involve sharing electrons. Noble gases can be forced into unstable
chemical compounds only under high pressure and temperature.
Group 17 (Group VII) contains the halogens, such as fluorine, chlorine, iodine and bromine, each of which has one less electron than a neighboring
noble gas. Each halogen has 5 p electrons (a p 5 configuration), while the p subshell can hold 6 electrons. This means the halogens have one
vacancy in their outermost subshell. They thus readily accept an extra electron (it becomes tightly bound, closing the shell as in noble gases) and are
highly reactive chemically. The halogens are also likely to form singly negative ions, such as C1− , fitting an extra electron into the vacancy in the
outer subshell. In contrast, alkali metals, such as sodium and potassium, all have a single s electron in their outermost subshell (an s 1
configuration) and are members of Group 1 (Group I). These elements easily give up their extra electron and are thus highly reactive chemically. As
you might expect, they also tend to form singly positive ions, such as Na+ , by losing their loosely bound outermost electron. They are metals
(conductors), because the loosely bound outer electron can move freely.
Of course, other groups are also of interest. Carbon, silicon, and germanium, for example, have similar chemistries and are in Group 4 (Group IV).
Carbon, in particular, is extraordinary in its ability to form many types of bonds and to be part of long chains, such as inorganic molecules. The large
group of what are called transitional elements is characterized by the filling of the d subshells and crossing of energy levels. Heavier groups, such
as the lanthanide series, are more complex—their shells do not fill in simple order. But the groups recognized by chemists such as Mendeleev have
an explanation in the substructure of atoms.
PhET Explorations: Build an Atom
Build an atom out of protons, neutrons, and electrons, and see how the element, charge, and mass change. Then play a game to test your ideas!
Figure 30.63 Build an Atom (http://cnx.org/content/m42618/1.4/build-an-atom_en.jar)
Glossary
angular momentum quantum number: a quantum number associated with the angular momentum of electrons
atom: basic unit of matter, which consists of a central, positively charged nucleus surrounded by negatively charged electrons
atomic de-excitation: process by which an atom transfers from an excited electronic state back to the ground state electronic configuration; often
occurs by emission of a photon
atomic excitation: a state in which an atom or ion acquires the necessary energy to promote one or more of its electrons to electronic states
higher in energy than their ground state
1102 CHAPTER 30 | ATOMIC PHYSICS
atomic number: the number of protons in the nucleus of an atom
Bohr radius: the mean radius of the orbit of an electron around the nucleus of a hydrogen atom in its ground state
Brownian motion: the continuous random movement of particles of matter suspended in a liquid or gas
cathode-ray tube: a vacuum tube containing a source of electrons and a screen to view images
double-slit interference: an experiment in which waves or particles from a single source impinge upon two slits so that the resulting interference
pattern may be observed
energies of hydrogen-like atoms: Bohr formula for energies of electron states in hydrogen-like atoms: En = − Z 2
n 2 E 0( n = 1, 2, 3, … )
energy-level diagram: a diagram used to analyze the energy level of electrons in the orbits of an atom
fine structure: the splitting of spectral lines of the hydrogen spectrum when the spectral lines are examined at very high resolution
fluorescence: any process in which an atom or molecule, excited by a photon of a given energy, de-excites by emission of a lower-energy photon
hologram: means entire picture (from the Greek word holo, as in holistic), because the image produced is three dimensional
holography: the process of producing holograms
hydrogen spectrum wavelengths:
⎛
⎞
the wavelengths of visible light from hydrogen; can be calculated by 1
λ = R⎜ 1
⎟
⎝ n 2 − 12
f
n i ⎠
hydrogen-like atom: any atom with only a single electron
intrinsic magnetic field: the magnetic field generated due to the intrinsic spin of electrons
intrinsic spin: the internal or intrinsic angular momentum of electrons
laser: acronym for light amplification by stimulated emission of radiation
magnitude of the intrinsic (internal) spin angular momentum: given by S = s( s + 1) h 2π
metastable: a state whose lifetime is an order of magnitude longer than the most short-lived states
orbital angular momentum: an angular momentum that corresponds to the quantum analog of classical angular momentum
orbital magnetic field: the magnetic field generated due to the orbital motion of electrons
Pauli exclusion principle: a principle that states that no two electrons can have the same set of quantum numbers; that is, no two electrons can
be in the same state
phosphorescence: the de-excitation of a metastable state
planetary model of the atom: the most familiar model or illustration of the structure of the atom
population inversion: the condition in which the majority of atoms in a sample are in a metastable state
quantum numbers: the values of quantized entities, such as energy and angular momentum
Rydberg constant: a physical constant related to the atomic spectra with an established value of 1.097×107 m−1
shell: a probability cloud for electrons that has a single principal quantum number
space quantization: the fact that the orbital angular momentum can have only certain directions
spin projection quantum number: quantum number that can be used to calculate the intrinsic electron angular momentum along the z -axis
spin quantum number: the quantum number that parameterizes the intrinsic angular momentum (or spin angular momentum, or simply spin) of a
given particle
stimulated emission: emission by atom or molecule in which an excited state is stimulated to decay, most readily caused by a photon of the
same energy that is necessary to excite the state
subshell: the probability cloud for electrons that has a single angular momentum quantum number l
x rays: a form of electromagnetic radiation
x-ray diffraction: a technique that provides the detailed information about crystallographic structure of natural and manufactured materials
CHAPTER 30 | ATOMIC PHYSICS 1103
Zeeman effect: the effect of external magnetic fields on spectral lines
z-component of spin angular momentum: component of intrinsic electron spin along the z -axis
z-component of the angular momentum: component of orbital angular momentum of electron along the z -axis
Section Summary
30.1 Discovery of the Atom
• Atoms are the smallest unit of elements; atoms combine to form molecules, the smallest unit of compounds.
• The first direct observation of atoms was in Brownian motion.
• Analysis of Brownian motion gave accurate sizes for atoms ( 10−10 m on average) and a precise value for Avogadro’s number.
30.2 Discovery of the Parts of the Atom: Electrons and Nuclei
• Atoms are composed of negatively charged electrons, first proved to exist in cathode-ray-tube experiments, and a positively charged nucleus.
• All electrons are identical and have a charge-to-mass ratio of
qe
m = − 1.76×1011 C/kg.
e
• The positive charge in the nuclei is carried by particles called protons, which have a charge-to-mass ratio of
qp
m = 9.57×107 C/kg.
p
• Mass of electron,
me = 9.11×10−31 kg.
• Mass of proton,
mp = 1.67×10−27 kg.
• The planetary model of the atom pictures electrons orbiting the nucleus in the same way that planets orbit the sun.
30.3 Bohr’s Theory of the Hydrogen Atom
• The planetary model of the atom pictures electrons orbiting the nucleus in the way that planets orbit the sun. Bohr used the planetary model to
develop the first reasonable theory of hydrogen, the simplest atom. Atomic and molecular spectra are quantized, with hydrogen spectrum
wavelengths given by the formula
1
⎛
⎞
λ = R⎜ 1
⎟,
⎝ n 2 − 12
f
n i ⎠
where λ is the wavelength of the emitted EM radiation and R is the Rydberg constant, which has the value
R = 1.097×107 m−1 .
• The constants n i and n f are positive integers, and n i must be greater than n f .
• Bohr correctly proposed that the energy and radii of the orbits of electrons in atoms are quantized, with energy for transitions between orbits
given by
Δ E = hf = E i − E f,
where Δ E is the change in energy between the initial and final orbits and hf is the energy of an absorbed or emitted photon. It is useful to
plot orbital energies on a vertical graph called an energy-level diagram.
• Bohr proposed that the allowed orbits are circular and must have quantized orbital angular momentum given by
L = mevrn = n h
2 π( n = 1, 2, 3 …),
where L is the angular momentum, rn is the radius of the nth orbit, and h is Planck’s constant. For all one-electron (hydrogen-like) atoms,
the radius of an orbit is given by
rn = n 2
Z a B(allowed orbits n = 1, 2, 3, ...),
Z is the atomic number of an element (the number of electrons is has when neutral) and a B is defined to be the Bohr radius, which is
a B =
h 2
4 π 2 m
2 = 0.529×10−10 m.
e kqe
• Furthermore, the energies of hydrogen-like atoms are given by
En = − Z 2
n 2 E 0( n = 1, 2, 3 ...),
where E 0 is the ground-state energy and is given by
4
E
me k 2
0 = 2π2 qeh 2
= 13.6 eV.
Thus, for hydrogen,
1104 CHAPTER 30 | ATOMIC PHYSICS
En = −13.6 eV
n 2 ( n, = , 1, 2, 3 ...).
• The Bohr Theory gives accurate values for the energy levels in hydrogen-like atoms, but it has been improved upon in several respects.
30.4 X Rays: Atomic Origins and Applications
• X rays are relatively high-frequency EM radiation. They are produced by transitions between inner-shell electron levels, which produce x rays
characteristic of the atomic element, or by accelerating electrons.
• X rays have many uses, including medical diagnostics and x-ray diffraction.
30.5 Applications of Atomic Excitations and De-Excitations
• An important atomic process is fluorescence, defined to be any process in which an atom or molecule is excited by absorbing a photon of a
given energy and de-excited by emitting a photon of a lower energy.
• Some states live much longer than others and are termed metastable.
• Phosphorescence is the de-excitation of a metastable state.
• Lasers produce coherent single-wavelength EM radiation by stimulated emission, in which a metastable state is stimulated to decay.
• Lasing requires a population inversion, in which a majority of the atoms or molecules are in their metastable state.
30.6 The Wave Nature of Matter Causes Quantization
• Quantization of orbital energy is caused by the wave nature of matter. Allowed orbits in atoms occur for constructive interference of electrons in
the orbit, requiring an integral number of wavelengths to fit in an orbit’s circumference; that is,
nλn = 2 πrn( n = 1, 2, 3 ...) ,
where λn is the electron’s de Broglie wavelength.
• Owing to the wave nature of electrons and the Heisenberg uncertainty principle, there are no well-defined orbits; rather, there are clouds of
probability.
• Bohr correctly proposed that the energy and radii of the orbits of electrons in atoms are quantized, with energy for transitions between orbits
given by
Δ E = hf = E i − E f,
where Δ E is the change in energy between the initial and final orbits and hf is the energy of an absorbed or emitted photon.
• It is useful to plot orbit energies on a vertical graph called an energy-level diagram.
• The allowed orbits are circular, Bohr proposed, and must have quantized orbital angular momentum given by
L = mevrn = n h
2π( n = 1, 2, 3 ...) ,
where L is the angular momentum, rn is the radius of orbit n , and h is Planck’s constant.
30.7 Patterns in Spectra Reveal More Quantization
• The Zeeman effect—the splitting of lines when a magnetic field is applied—is caused by other quantized entities in atoms.
• Both the magnitude and direction of orbital angular momentum are quantized.
• The same is true for the magnitude and direction of the intrinsic spin of electrons.
30.8 Quantum Numbers and Rules
• Quantum numbers are used to express the allowed values of quantized entities. The principal quantum number n labels the basic states of a
system and is given by
n = 1, 2, 3,....
• The magnitude of angular momentum is given by
L = l( l + 1) h
2π ( l = 0, 1, 2, ... , n − 1) ,
where l is the angular momentum quantum number. The direction of angular momentum is quantized, in that its component along an axis
defined by a magnetic field, called the z -axis is given by
L
h
z = m
⎛
l 2π ⎝ ml = − l, − l + 1, ... , − 1, 0, 1, ... l − 1, l⎞⎠,
where Lz is the z -component of the angular momentum and ml is the angular momentum projection quantum number. Similarly, the
electron’s intrinsic spin angular momentum S is given by
S = s( s + 1) h
2π ( s = 1 / 2 for electrons),
s is defined to be the spin quantum number. Finally, the direction of the electron’s spin along the z -axis is given by
S
h ⎛
⎞
z = ms 2π ⎝ ms = −12 , + 12⎠,
where Sz is the z -component of spin angular momentum and ms is the spin projection quantum number. Spin projection ms =+1 / 2 is
referred to as spin up, whereas ms = −1 / 2 is called spin down. Table 30.1 summarizes the atomic quantum numbers and their allowed
values.
30.9 The Pauli Exclusion Principle
• The state of a system is completely described by a complete set of quantum numbers. This set is written as ⎛⎝ n, l, ml , ms⎞⎠ .
CHAPTER 30 | ATOMIC PHYSICS 1105
• The Pauli exclusion principle says that no two electrons can have the same set of quantum numbers; that is, no two electrons can be in the
same state.
• This exclusion limits the number of electrons in atomic shells and subshells. Each value of n corresponds to a shell, and each value of l
corresponds to a subshell.
• The maximum number of electrons that can be in a subshell is 2(2 l + 1) .
• The maximum number of electrons that can be in a shell is 2 n 2 .
Conceptual Questions
30.1 Discovery of the Atom
1. Name three different types of evidence for the existence of atoms.
2. Explain why patterns observed in the periodic table of the elements are evidence for the existence of atoms, and why Brownian motion is a more
direct type of evidence for their existence.
3. If atoms exist, why can’t we see them with visible light?
30.2 Discovery of the Parts of the Atom: Electrons and Nuclei
4. What two pieces of evidence allowed the first calculation of me , the mass of the electron?
(a) The ratios qe / me and q p / m p .
(b) The values of qe and EB .
(c) The ratio qe / me and qe .
Justify your response.
5. How do the allowed orbits for electrons in atoms differ from the allowed orbits for planets around the sun? Explain how the correspondence





