combinations of the primary colors produce all the hues.
• The true color of an object is related to its relative absorption of various wavelengths of light. The color of a light source is related to the
wavelengths it produces.
• Color constancy is the ability of the eye-brain system to discern the true color of an object illuminated by various light sources.
• The retinex theory of color vision explains color constancy by postulating the existence of three retinexes or image systems, associated with the
three types of cones that are compared to obtain sophisticated information.
26.4 Microscopes
• The microscope is a multiple-element system having more than a single lens or mirror.
• Many optical devices contain more than a single lens or mirror. These are analysed by considering each element sequentially. The image
formed by the first is the object for the second, and so on. The same ray tracing and thin lens techniques apply to each lens element.
• The overall magnification of a multiple-element system is the product of the magnifications of its individual elements. For a two-element system
with an objective and an eyepiece, this is
m = m o m e,
where m o is the magnification of the objective and m e is the magnification of the eyepiece, such as for a microscope.
• Microscopes are instruments for allowing us to see detail we would not be able to see with the unaided eye and consist of a range of
components.
• The eyepiece and objective contribute to the magnification. The numerical aperture ( NA) of an objective is given by
NA = n sin α
where n is the refractive index and α the angle of acceptance.
• Immersion techniques are often used to improve the light gathering ability of microscopes. The specimen is illuminated by transmitted, scattered
or reflected light though a condenser.
• The f /# describes the light gathering ability of a lens. It is given by
f /# = fD ≈ 1
2 NA.
26.5 Telescopes
• Simple telescopes can be made with two lenses. They are used for viewing objects at large distances and utilize the entire range of the
electromagnetic spectrum.
• The angular magnification M for a telescope is given by
M = θ′ θ = − f o f,e
where θ is the angle subtended by an object viewed by the unaided eye, θ′ is the angle subtended by a magnified image, and f o and f e
are the focal lengths of the objective and the eyepiece.
26.6 Aberrations
• Aberrations or image distortions can arise due to the finite thickness of optical instruments, imperfections in the optical components, and
limitations on the ways in which the components are used.
• The means for correcting aberrations range from better components to computational techniques.
Conceptual Questions
26.1 Physics of the Eye
1. If the lens of a person’s eye is removed because of cataracts (as has been done since ancient times), why would you expect a spectacle lens of
about 16 D to be prescribed?
2. A cataract is cloudiness in the lens of the eye. Is light dispersed or diffused by it?
3. When laser light is shone into a relaxed normal-vision eye to repair a tear by spot-welding the retina to the back of the eye, the rays entering the
eye must be parallel. Why?
4. How does the power of a dry contact lens compare with its power when resting on the tear layer of the eye? Explain.
5. Why is your vision so blurry when you open your eyes while swimming under water? How does a face mask enable clear vision?
26.2 Vision Correction
6. It has become common to replace the cataract-clouded lens of the eye with an internal lens. This intraocular lens can be chosen so that the person
has perfect distant vision. Will the person be able to read without glasses? If the person was nearsighted, is the power of the intraocular lens greater
or less than the removed lens?
7. If the cornea is to be reshaped (this can be done surgically or with contact lenses) to correct myopia, should its curvature be made greater or
smaller? Explain. Also explain how hyperopia can be corrected.
CHAPTER 26 | VISION AND OPTICAL INSTRUMENTS 953
8. If there is a fixed percent uncertainty in LASIK reshaping of the cornea, why would you expect those people with the greatest correction to have a
poorer chance of normal distant vision after the procedure?
9. A person with presbyopia has lost some or all of the ability to accommodate the power of the eye. If such a person’s distant vision is corrected with
LASIK, will she still need reading glasses? Explain.
26.3 Color and Color Vision
10. A pure red object on a black background seems to disappear when illuminated with pure green light. Explain why.
11. What is color constancy, and what are its limitations?
12. There are different types of color blindness related to the malfunction of different types of cones. Why would it be particularly useful to study those
rare individuals who are color blind only in one eye or who have a different type of color blindness in each eye?
13. Propose a way to study the function of the rods alone, given they can sense light about 1000 times dimmer than the cones.
26.4 Microscopes
14. Geometric optics describes the interaction of light with macroscopic objects. Why, then, is it correct to use geometric optics to analyse a
microscope’s image?
15. The image produced by the microscope in Figure 26.16 cannot be projected. Could extra lenses or mirrors project it? Explain.
16. Why not have the objective of a microscope form a case 2 image with a large magnification? (Hint: Consider the location of that image and the
difficulty that would pose for using the eyepiece as a magnifier.)
17. What advantages do oil immersion objectives offer?
18. How does the NA of a microscope compare with the NA of an optical fiber?
26.5 Telescopes
19. If you want your microscope or telescope to project a real image onto a screen, how would you change the placement of the eyepiece relative to
the objective?
26.6 Aberrations
20. List the various types of aberrations. What causes them and how can each be reduced?
954 CHAPTER 26 | VISION AND OPTICAL INSTRUMENTS
Problems & Exercises
19. Repeat the previous problem for glasses that are 1.75 cm from the
eyes.
26.1 Physics of the Eye
20. The contact lens prescription for a mildly farsighted person is 0.750
D, and the person has a near point of 29.0 cm. What is the power of the
Unless otherwise stated, the lens-to-retina distance is 2.00 cm.
tear layer between the cornea and the lens if the correction is ideal,
1. What is the power of the eye when viewing an object 50.0 cm away?
taking the tear layer into account?
2. Calculate the power of the eye when viewing an object 3.00 m away.
21. A nearsighted man cannot see objects clearly beyond 20 cm from his
eyes. How close must he stand to a mirror in order to see what he is
3. (a) The print in many books averages 3.50 mm in height. How high is
doing when he shaves?
the image of the print on the retina when the book is held 30.0 cm from
the eye?
22. A mother sees that her child’s contact lens prescription is 0.750 D.
What is the child’s near point?
(b) Compare the size of the print to the sizes of rods and cones in the
fovea and discuss the possible details observable in the letters. (The eye- 23. Repeat the previous problem for glasses that are 2.20 cm from the
brain system can perform better because of interconnections and higher
eyes.
order image processing.)
24. The contact lens prescription for a nearsighted person is –4.00 D
4. Suppose a certain person’s visual acuity is such that he can see
and the person has a far point of 22.5 cm. What is the power of the tear
objects clearly that form an image 4.00 μm high on his retina. What is
layer between the cornea and the lens if the correction is ideal, taking the
the maximum distance at which he can read the 75.0 cm high letters on
tear layer into account?
the side of an airplane?
25. Unreasonable Results
5. People who do very detailed work close up, such as jewellers, often
A boy has a near point of 50 cm and a far point of 500 cm. Will a
can see objects clearly at much closer distance than the normal 25 cm.
–4.00 D lens correct his far point to infinity?
(a) What is the power of the eyes of a woman who can see an object
clearly at a distance of only 8.00 cm?
26.4 Microscopes
(b) What is the size of an image of a 1.00 mm object, such as lettering
26. A microscope with an overall magnification of 800 has an objective
inside a ring, held at this distance?
that magnifies by 200. (a) What is the magnification of the eyepiece? (b)
(c) What would the size of the image be if the object were held at the
If there are two other objectives that can be used, having magnifications
normal 25.0 cm distance?
of 100 and 400, what other total magnifications are possible?
27. (a) What magnification is produced by a 0.150 cm focal length
26.2 Vision Correction
microscope objective that is 0.155 cm from the object being viewed? (b)
6. What is the far point of a person whose eyes have a relaxed power of
What is the overall magnification if an 8× eyepiece (one that produces a
50.5 D?
magnification of 8.00) is used?
7. What is the near point of a person whose eyes have an
28. (a) Where does an object need to be placed relative to a microscope
accommodated power of 53.5 D?
for its 0.500 cm focal length objective to produce a magnification of
–400 ? (b) Where should the 5.00 cm focal length eyepiece be placed to
8. (a) A laser vision correction reshaping the cornea of a myopic patient
reduces the power of his eye by 9.00 D, with a ±5.0% uncertainty in the produce a further fourfold (4.00) magnification?
final correction. What is the range of diopters for spectacle lenses that
29. You switch from a 1.40 NA 60× oil immersion objective to a
this person might need after LASIK procedure? (b) Was the person
1.40 NA 60× oil immersion objective. What are the acceptance angles
nearsighted or farsighted before the procedure? How do you know?
for each? Compare and comment on the values. Which would you use
9. In a LASIK vision correction, the power of a patient’s eye is increased
first to locate the target area on your specimen?
by 3.00 D. Assuming this produces normal close vision, what was the
30. An amoeba is 0.305 cm away from the 0.300 cm focal length
patient’s near point before the procedure?
objective lens of a microscope. (a) Where is the image formed by the
10. What was the previous far point of a patient who had laser vision
objective lens? (b) What is this image’s magnification? (c) An eyepiece
correction that reduced the power of her eye by 7.00 D, producing normal with a 2.00 cm focal length is placed 20.0 cm from the objective. Where
distant vision for her?
is the final image? (d) What magnification is produced by the eyepiece?
11. A severely myopic patient has a far point of 5.00 cm. By how many
(e) What is the overall magnification? (See Figure 26.16.)
diopters should the power of his eye be reduced in laser vision correction
31. You are using a standard microscope with a 0.10 NA 4× objective
to obtain normal distant vision for him?
and switch to a 0.65 NA 40× objective. What are the acceptance
12. A student’s eyes, while reading the blackboard, have a power of 51.0
angles for each? Compare and comment on the values. Which would you
D. How far is the board from his eyes?
use first to locate the target area on of your specimen? (See Figure
13. The power of a physician’s eyes is 53.0 D while examining a patient.
26.17.)
How far from her eyes is the feature being examined?
32. Unreasonable Results
14. A young woman with normal distant vision has a 10.0% ability to
Your friends show you an image through a microscope. They tell you that
accommodate (that is, increase) the power of her eyes. What is the
the microscope has an objective with a 0.500 cm focal length and an
closest object she can see clearly?
eyepiece with a 5.00 cm focal length. The resulting overall magnification
15. The far point of a myopic administrator is 50.0 cm. (a) What is the
is 250,000. Are these viable values for a microscope?
relaxed power of his eyes? (b) If he has the normal 8.00% ability to
accommodate, what is the closest object he can see clearly?
26.5 Telescopes
16. A very myopic man has a far point of 20.0 cm. What power contact
Unless otherwise stated, the lens-to-retina distance is 2.00 cm.
lens (when on the eye) will correct his distant vision?
33. What is the angular magnification of a telescope that has a 100 cm
17. Repeat the previous problem for eyeglasses held 1.50 cm from the
focal length objective and a 2.50 cm focal length eyepiece?
eyes.
34. Find the distance between the objective and eyepiece lenses in the
18. A myopic person sees that her contact lens prescription is –4.00 D . telescope in the above problem needed to produce a final image very far
What is her far point?
CHAPTER 26 | VISION AND OPTICAL INSTRUMENTS 955
from the observer, where vision is most relaxed. Note that a telescope is
normally used to view very distant objects.
35. A large reflecting telescope has an objective mirror with a 10.0 m
radius of curvature. What angular magnification does it produce when a
3.00 m focal length eyepiece is used?
36. A small telescope has a concave mirror with a 2.00 m radius of
curvature for its objective. Its eyepiece is a 4.00 cm focal length lens. (a)
What is the telescope’s angular magnification? (b) What angle is
subtended by a 25,000 km diameter sunspot? (c) What is the angle of its
telescopic image?
37. A 7.5× binocular produces an angular magnification of −7.50 ,
acting like a telescope. (Mirrors are used to make the image upright.) If
the binoculars have objective lenses with a 75.0 cm focal length, what is
the focal length of the eyepiece lenses?
38. Construct Your Own Problem
Consider a telescope of the type used by Galileo, having a convex
objective and a concave eyepiece as illustrated in Figure 26.23(a).
Construct a problem in which you calculate the location and size of the
image produced. Among the things to be considered are the focal lengths
of the lenses and their relative placements as well as the size and
location of the object. Verify that the angular magnification is greater than
one. That is, the angle subtended at the eye by the image is greater than
the angle subtended by the object.
26.6 Aberrations
39. Integrated Concepts
(a) During laser vision correction, a brief burst of 193 nm ultraviolet light
is projected onto the cornea of the patient. It makes a spot 1.00 mm in
diameter and deposits 0.500 mJ of energy. Calculate the depth of the
layer ablated, assuming the corneal tissue has the same properties as
water and is initially at 34.0ºC . The tissue’s temperature is increased to
100ºC and evaporated without further temperature increase.
(b) Does your answer imply that the shape of the cornea can be finely
controlled?
956 CHAPTER 26 | VISION AND OPTICAL INSTRUMENTS

CHAPTER 27 | WAVE OPTICS 957
27
WAVE OPTICS
Figure 27.1 The colors reflected by this compact disc vary with angle and are not caused by pigments. Colors such as these are direct evidence of the wave character of light.
(credit: Infopro, Wikimedia Commons)
Learning Objectives
27.1. The Wave Aspect of Light: Interference
• Discuss the wave character of light.
• Identify the changes when light enters a medium.
27.2. Huygens's Principle: Diffraction
• Discuss the propagation of transverse waves.
• Discuss Huygens’s principle.
• Explain the bending of light.
27.3. Young’s Double Slit Experiment
• Explain the phenomena of interference.
• Define constructive interference for a double slit and destructive interference for a double slit.
27.4. Multiple Slit Diffraction
• Discuss the pattern obtained from diffraction grating.
• Explain diffraction grating effects.
27.5. Single Slit Diffraction
• Discuss the single slit diffraction pattern.
27.6. Limits of Resolution: The Rayleigh Criterion
• Discuss the Rayleigh criterion.
27.7. Thin Film Interference
• Discuss the rainbow formation by thin films.
27.8. Polarization
• Discuss the meaning of polarization.
• Discuss the property of optical activity of certain materials.
27.9. *Extended Topic* Microscopy Enhanced by the Wave Characteristics of Light
• Discuss the different types of microscopes.

958 CHAPTER 27 | WAVE OPTICS
Introduction to Wave Optics
Examine a compact disc under white light, noting the colors observed and locations of the colors. Determine if the spectra are formed by diffraction
from circular lines centered at the middle of the disc and, if so, what is their spacing. If not, determine the type of spacing. Also with the CD, explore
the spectra of a few light sources, such as a candle flame, incandescent bulb, halogen light, and fluorescent light. Knowing the spacing of the rows of
pits in the compact disc, estimate the maximum spacing that will allow the given number of megabytes of information to be stored.
If you have ever looked at the reds, blues, and greens in a sunlit soap bubble and wondered how straw-colored soapy water could produce them, you
have hit upon one of the many phenomena that can only be explained by the wave character of light (see Figure 27.2). The same is true for the
colors seen in an oil slick or in the light reflected from a compact disc. These and other interesting phenomena, such as the dispersion of white light
into a rainbow of colors when passed through a narrow slit, cannot be explained fully by geometric optics. In these cases, light interacts with small
objects and exhibits its wave characteristics. The branch of optics that considers the behavior of light when it exhibits wave characteristics
(particularly when it interacts with small objects) is called wave optics (sometimes called physical optics). It is the topic of this chapter.
Figure 27.2 These soap bubbles exhibit brilliant colors when exposed to sunlight. How are the colors produced if they are not pigments in the soap? (credit: Scott Robinson,
Flickr)
27.1 The Wave Aspect of Light: Interference
We know that visible light is the type of electromagnetic wave to which our eyes respond. Like all other electromagnetic waves, it obeys the equation
c
(27.1)
= f λ,
where c = 3×108 m/s is the speed of light in vacuum, f is the frequency of the electromagnetic waves, and λ is its wavelength. The range of
visible wavelengths is approximately 380 to 760 nm. As is true for all waves, light travels in straight lines and acts like a ray when it interacts with
objects several times as large as its wavelength. However, when it interacts with smaller objects, it displays its wave characteristics prominently.
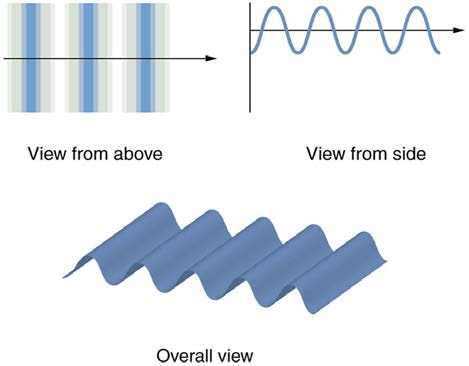
Interference is the hallmark of a wave, and in Figure 27.3 both the ray and wave characteristics of light can be seen. The laser beam emitted by the observatory epitomizes a ray, traveling in a straight line. However, passing a pure-wavelength beam through vertical slits with a size close to the
wavelength of the beam reveals the wave character of light, as the beam spreads out horizontally into a pattern of bright and dark regions caused by
systematic constructive and destructive interference. Rather than spreading out, a ray would continue traveling straight ahead after passing through
slits.
Making Connections: Waves
The most certain indication of a wave is interference. This wave characteristic is most prominent when the wave interacts with an object that is
not large compared with the wavelength. Interference is observed for water waves, sound waves, light waves, and (as we will see in Special
Relativity) for matter waves, such as electrons scattered from a crystal.

CHAPTER 27 | WAVE OPTICS 959
Figure 27.3 (a) The laser beam emitted by an observatory acts like a ray, traveling in a straight line. This laser beam is from the Paranal Observatory of the European
Southern Observatory. (credit: Yuri Beletsky, European Southern Observatory) (b) A laser beam passing through a grid of vertical slits produces an interference
pattern—characteristic of a wave. (credit: Shim'on and Slava Rybka, Wikimedia Commons)
Light has wave characteristics in various media as well as in a vacuum. When light goes from a vacuum to some medium, like water, its speed and
wavelength change, but its frequency f remains the same. (We can think of light as a forced oscillation that must have the frequency of the original
source.) The speed of light in a medium is v = c / n , where n is its index of refraction. If we divide both sides of equation c = <







