this applied voltage?
potential difference of 1.00×102 MV . (a) What energy was
18. The voltage across a membrane forming a cell wall is 80.0 mV and
dissipated? (b) What mass of water could be raised from 15ºC to the
the membrane is 9.00 nm thick. What is the electric field strength? (The
boiling point and then boiled by this energy? (c) Discuss the damage that
value is surprisingly large, but correct. Membranes are discussed in
could be caused to the tree by the expansion of the boiling steam.
Capacitors and Dielectrics and Nerve
Conduction—Electrocardiograms.) You may assume a uniform electric
8. Integrated Concepts
field.
A 12.0 V battery-operated bottle warmer heats 50.0 g of glass,
19. Membrane walls of living cells have surprisingly large electric fields
2.50×102 g of baby formula, and 2.00×102 g of aluminum from
across them due to separation of ions. (Membranes are discussed in
20.0ºC to 90.0ºC . (a) How much charge is moved by the battery? (b) some detail in Nerve Conduction—Electrocardiograms.) What is the
voltage across an 8.00 nm–thick membrane if the electric field strength
How many electrons per second flow if it takes 5.00 min to warm the
across it is 5.50 MV/m? You may assume a uniform electric field.
formula? (Hint: Assume that the specific heat of baby formula is about the
same as the specific heat of water.)
20. Two parallel conducting plates are separated by 10.0 cm, and one of
them is taken to be at zero volts. (a) What is the electric field strength
9. Integrated Concepts
between them, if the potential 8.00 cm from the zero volt plate (and 2.00
A battery-operated car utilizes a 12.0 V system. Find the charge the
cm from the other) is 450 V? (b) What is the voltage between the plates?
batteries must be able to move in order to accelerate the 750 kg car from
21. Find the maximum potential difference between two parallel
rest to 25.0 m/s, make it climb a 2.00×102 m high hill, and then cause
conducting plates separated by 0.500 cm of air, given the maximum
it to travel at a constant 25.0 m/s by exerting a 5.00×102 N force for
sustainable electric field strength in air to be 3.0×106 V/m .
an hour.
22. A doubly charged ion is accelerated to an energy of 32.0 keV by the
10. Integrated Concepts
electric field between two parallel conducting plates separated by 2.00
cm. What is the electric field strength between the plates?
Fusion probability is greatly enhanced when appropriate nuclei are
brought close together, but mutual Coulomb repulsion must be overcome. 23. An electron is to be accelerated in a uniform electric field having a
This can be done using the kinetic energy of high-temperature gas ions
strength of 2.00×106 V/m . (a) What energy in keV is given to the
or by accelerating the nuclei toward one another. (a) Calculate the
electron if it is accelerated through 0.400 m? (b) Over what distance
potential energy of two singly charged nuclei separated by
would it have to be accelerated to increase its energy by 50.0 GeV?
1.00 × 10–12 m by finding the voltage of one at that distance and
multiplying by the charge of the other. (b) At what temperature will atoms
19.3 Electrical Potential Due to a Point Charge
of a gas have an average kinetic energy equal to this needed electrical
24. A 0.500 cm diameter plastic sphere, used in a static electricity
potential energy?
demonstration, has a uniformly distributed 40.0 pC charge on its surface.
11. Unreasonable Results
What is the potential near its surface?

CHAPTER 19 | ELECTRIC POTENTIAL AND ELECTRIC FIELD 691
25. What is the potential 0.530×10–10 m from a proton (the average
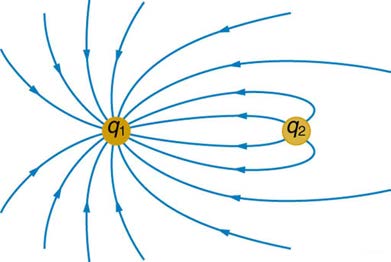
38. Figure 19.28 shows the electric field lines near two charges q 1 and
distance between the proton and electron in a hydrogen atom)?
q 2 , the first having a magnitude four times that of the second. Sketch
26. (a) A sphere has a surface uniformly charged with 1.00 C. At what
the equipotential lines for these two charges, and indicate the direction of
distance from its center is the potential 5.00 MV? (b) What does your
increasing potential.
answer imply about the practical aspect of isolating such a large charge?
39. Sketch the equipotential lines a long distance from the charges
27. How far from a 1.00 µC point charge will the potential be 100 V? At
shown in Figure 19.28. Indicate the direction of increasing potential.
what distance will it be 2.00×102 V?
28. What are the sign and magnitude of a point charge that produces a
potential of –2.00 V at a distance of 1.00 mm?
29. If the potential due to a point charge is 5.00×102 V at a distance of
15.0 m, what are the sign and magnitude of the charge?
30. In nuclear fission, a nucleus splits roughly in half. (a) What is the
potential 2.00×10 – 14 m from a fragment that has 46 protons in it? (b)
What is the potential energy in MeV of a similarly charged fragment at
this distance?
31. A research Van de Graaff generator has a 2.00-m-diameter metal
Figure 19.28 The electric field near two charges.
sphere with a charge of 5.00 mC on it. (a) What is the potential near its
40. Sketch the equipotential lines in the vicinity of two opposite charges,
surface? (b) At what distance from its center is the potential 1.00 MV? (c)
where the negative charge is three times as great in magnitude as the
An oxygen atom with three missing electrons is released near the Van de
positive. See Figure 19.28 for a similar situation. Indicate the direction of
Graaff generator. What is its energy in MeV at this distance?
increasing potential.
32. An electrostatic paint sprayer has a 0.200-m-diameter metal sphere
41. Sketch the equipotential lines in the vicinity of the negatively charged
at a potential of 25.0 kV that repels paint droplets onto a grounded object. conductor in Figure 19.29. How will these equipotentials look a long
(a) What charge is on the sphere? (b) What charge must a 0.100-mg
distance from the object?
drop of paint have to arrive at the object with a speed of 10.0 m/s?
33. In one of the classic nuclear physics experiments at the beginning of
the 20th century, an alpha particle was accelerated toward a gold
nucleus, and its path was substantially deflected by the Coulomb
interaction. If the energy of the doubly charged alpha nucleus was 5.00
MeV, how close to the gold nucleus (79 protons) could it come before
Figure 19.29 A negatively charged conductor.
being deflected?
42. Sketch the equipotential lines surrounding the two conducting plates
34. (a) What is the potential between two points situated 10 cm and 20
shown in Figure 19.30, given the top plate is positive and the bottom
cm from a 3.0 µC point charge? (b) To what location should the point at plate has an equal amount of negative charge. Be certain to indicate the
20 cm be moved to increase this potential difference by a factor of two?
distribution of charge on the plates. Is the field strongest where the plates
are closest? Why should it be?
35. Unreasonable Results
(a) What is the final speed of an electron accelerated from rest through a
voltage of 25.0 MV by a negatively charged Van de Graaff terminal?
(b) What is unreasonable about this result?
(c) Which assumptions are responsible?
19.4 Equipotential Lines
36. (a) Sketch the equipotential lines near a point charge + q . Indicate
Figure 19.30
the direction of increasing potential. (b) Do the same for a point charge
– 3 q .
43. (a) Sketch the electric field lines in the vicinity of the charged insulator
in Figure 19.31. Note its non-uniform charge distribution. (b) Sketch
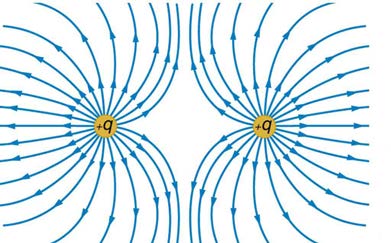
37. Sketch the equipotential lines for the two equal positive charges
equipotential lines surrounding the insulator. Indicate the direction of
shown in Figure 19.27. Indicate the direction of increasing potential.
increasing potential.
Figure 19.27 The electric field near two equal positive charges is directed away from
each of the charges.
Figure 19.31 A charged insulating rod such as might be used in a classroom
demonstration.

692 CHAPTER 19 | ELECTRIC POTENTIAL AND ELECTRIC FIELD
44. The naturally occurring charge on the ground on a fine day out in the
open country is –1.00 nC/m2 . (a) What is the electric field relative to
ground at a height of 3.00 m? (b) Calculate the electric potential at this
height. (c) Sketch electric field and equipotential lines for this scenario.
45. The lesser electric ray ( Narcine bancroftii) maintains an incredible
charge on its head and a charge equal in magnitude but opposite in sign
on its tail (Figure 19.32). (a) Sketch the equipotential lines surrounding
the ray. (b) Sketch the equipotentials when the ray is near a ship with a
conducting surface. (c) How could this charge distribution be of use to the
ray?
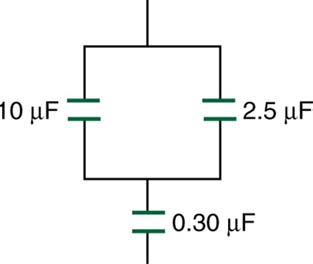
Figure 19.33 A combination of series and parallel connections of capacitors.
58. Suppose you want a capacitor bank with a total capacitance of 0.750
F and you possess numerous 1.50 mF capacitors. What is the smallest
number you could hook together to achieve your goal, and how would
you connect them?
59. What total capacitances can you make by connecting a 5.00 µF and
an 8.00 µF capacitor together?
60. Find the total capacitance of the combination of capacitors shown in
Figure 19.34.
Figure 19.32 Lesser electric ray ( Narcine bancroftii) (credit: National Oceanic and
Atmospheric Administration, NOAA's Fisheries Collection).
19.5 Capacitors and Dielectrics
46. What charge is stored in a 180 µF capacitor when 120 V is applied
to it?
47. Find the charge stored when 5.50 V is applied to an 8.00 pF
capacitor.
48. What charge is stored in the capacitor in Example 19.8?
49. Calculate the voltage applied to a 2.00 µF capacitor when it holds
Figure 19.34 A combination of series and parallel connections of capacitors.
3.10 µC
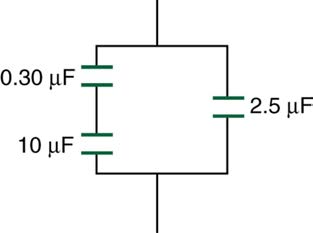
61. Find the total capacitance of the combination of capacitors shown in
of charge.
Figure 19.35.
50. What voltage must be applied to an 8.00 nF capacitor to store 0.160
mC of charge?
51. What capacitance is needed to store 3.00 µC of charge at a voltage
of 120 V?
52. What is the capacitance of a large Van de Graaff generator’s
terminal, given that it stores 8.00 mC of charge at a voltage of 12.0 MV?
53. Find the capacitance of a parallel plate capacitor having plates of
area 5.00 m2 that are separated by 0.100 mm of Teflon.
54. (a)What is the capacitance of a parallel plate capacitor having plates
Figure 19.35 A combination of series and parallel connections of capacitors.
of area 1.50 m2 that are separated by 0.0200 mm of neoprene rubber?
(b) What charge does it hold when 9.00 V is applied to it?
62. Unreasonable Results
55. Integrated Concepts
(a) An 8.00 µF capacitor is connected in parallel to another capacitor,
A prankster applies 450 V to an 80.0 µF capacitor and then tosses it to
producing a total capacitance of 5.00 µF . What is the capacitance of
an unsuspecting victim. The victim’s finger is burned by the discharge of
the second capacitor? (b) What is unreasonable about this result? (c)
the capacitor through 0.200 g of flesh. What is the temperature increase
Which assumptions are unreasonable or inconsistent?
of the flesh? Is it reasonable to assume no phase change?
56. Unreasonable Results
19.7 Energy Stored in Capacitors
63. (a) What is the energy stored in the 10.0 μF capacitor of a heart
(a) A certain parallel plate capacitor has plates of area 4.00 m2 ,
separated by 0.0100 mm of nylon, and stores 0.170 C of charge. What is
defibrillator charged to 9.00×103 V ? (b) Find the amount of stored
the applied voltage? (b) What is unreasonable about this result? (c)
charge.
Which assumptions are responsible or inconsistent?
64. In open heart surgery, a much smaller amount of energy will
19.6 Capacitors in Series and Parallel
defibrillate the heart. (a) What voltage is applied to the 8.00 μF
capacitor of a heart defibrillator that stores 40.0 J of energy? (b) Find the
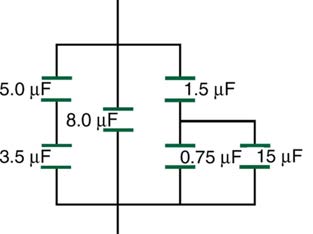
57. Find the total capacitance of the combination of capacitors in Figure
amount of stored charge.
19.33.
CHAPTER 19 | ELECTRIC POTENTIAL AND ELECTRIC FIELD 693
65. A 165 µF capacitor is used in conjunction with a motor. How much
energy is stored in it when 119 V is applied?
66. Suppose you have a 9.00 V battery, a 2.00 μF capacitor, and a
7.40 μF capacitor. (a) Find the charge and energy stored if the
capacitors are connected to the battery in series. (b) Do the same for a
parallel connection.
67. A nervous physicist worries that the two metal shelves of his wood
frame bookcase might obtain a high voltage if charged by static
electricity, perhaps produced by friction. (a) What is the capacitance of
the empty shelves if they have area 1.00×102 m2 and are 0.200 m
apart? (b) What is the voltage between them if opposite charges of
magnitude 2.00 nC are placed on them? (c) To show that this voltage
poses a small hazard, calculate the energy stored.
68. Show that for a given dielectric material the maximum energy a
parallel plate capacitor can store is directly proportional to the volume of
dielectric ( Volume = A · d ). Note that the applied voltage is limited by
the dielectric strength.
69. Construct Your Own Problem
Consider a heart defibrillator similar to that discussed in Example 19.11.
Construct a problem in which you examine the charge stored in the
capacitor of a defibrillator as a function of stored energy. Among the
things to be considered are the applied voltage and whether it should
vary with energy to be delivered, the range of energies involved, and the
capacitance of the defibrillator. You may also wish to consider the much
smaller energy needed for defibrillation during open-heart surgery as a
variation on this problem.
70. Unreasonable Results
(a) On a particular day, it takes 9.60×103 J of electric energy to start a
truck’s engine. Calculate the capacitance of a capacitor that could store
that amount of energy at 12.0 V. (b) What is unreasonable about this
result? (c) Which assumptions are responsible?
694 CHAPTER 19 | ELECTRIC POTENTIAL AND ELECTRIC FIELD

CHAPTER 20 | ELECTRIC CURRENT, RESISTANCE, AND OHM'S LAW 695
20
ELECTRIC CURRENT, RESISTANCE, AND OHM'S
LAW
Figure 20.1 Electric energy in massive quantities is transmitted from this hydroelectric facility, the Srisailam power station located along the Krishna River in India, by the
movement of charge—that is, by electric current. (credit: Chintohere, Wikimedia Commons)
696 CHAPTER 20 | ELECTRIC CURRENT, RESISTANCE, AND OHM'S LAW
Learning Objectives
20.1. Current
• Define electric current, ampere, and drift velocity
• Describe the direction of charge flow in conventional current.
• Use drift velocity to calculate current and vice versa.
20.2. Ohm’s Law: Resistance and Simple Circuits
• Explain the origin of Ohm’s law.
• Calculate voltages, currents, or resistances with Ohm’s law.
• Explain what an ohmic material is.
• Describe a simple circuit.
20.3. Resistance and Resistivity
• Explain the concept of resistivity.
• Use resistivity to calculate the resistance of specified configurations of material.
• Use the thermal coefficient of resistivity to calculate the change of resistance with temperature.
20.4. Electric Power and Energy
• Calculate the power dissipated by a resistor and power supplied by a power supply.
• Calculate the cost of electricity under various circumstances.
20.5. Alternating Current versus Direct Current
• Explain the differences and similarities between AC and DC current.
• Calculate rms voltage, current, and average power.
• Explain why AC current is used for power transmission.
20.6. Electric Hazards and the Human Body
• Define thermal hazard, shock hazard, and short circuit.
• Explain what effects various levels of current have on the human body.
20.7. Nerve Conduction–Electrocardiograms
• Explain the process by which electric signals are transmitted along a neuron.
• Explain the effects myelin sheaths have on signal propagation.
• Explain what the features of an ECG signal indicate.
Introduction to Electric Current, Resistance, and Ohm's Law
The flicker of numbers on a handheld calculator, nerve impulses carrying signals of vision to the brain, an ultrasound device sending a signal to a
computer screen, the brain sending a message for a baby to twitch its toes, an electric train pulling its load over a mountain pass, a hydroelectric
plant sending energy to metropolitan and rural users—these and many other examples of electricity involve electric current, the movement of charge.
Humankind has indeed harnessed electricity, the basis of technology, to improve our quality of life. Whereas the previous two chapters concentrated
on static electricity and the fundamental force underlying its behavior, the next few chapters will be devoted to electric and magnetic phenomena
involving current. In addition to exploring applications of electricity, we shall gain new insights into nature—in particular, the fact that all magnetism
results from electric current.
20.1 Current
Electric Current
Electric current is defined to be the rate at which charge flows. A large current, such as that used to start a truck engine, moves a large amount of
charge in a small time, whereas a small current, such as that used to operate a hand-held calculator, moves a small amount of charge over a long
period of time. In equation form, electric current I is defined to be
(20.1)
I = Δ Q
Δ t ,
where Δ Q is the amount of charge passing through a given area in time Δ t . (As in previous chapters, initial time is often taken to be zero, in which
case Δ t = t .) (See Figure 20.2.) The SI unit for current is the ampere (A), named for the French physicist André-Marie Ampère (1775–1836). Since I = Δ Q / Δ t , we see that an ampere is one coulomb per second:
(20.2)
1 A = 1 C/s
Not only are fuses and circuit breakers rated in amperes (or amps), so are many electrical appliances.
Figure 20.2 The rate of flow of charge is current. An ampere is the flow of one coulomb through an area in one second.
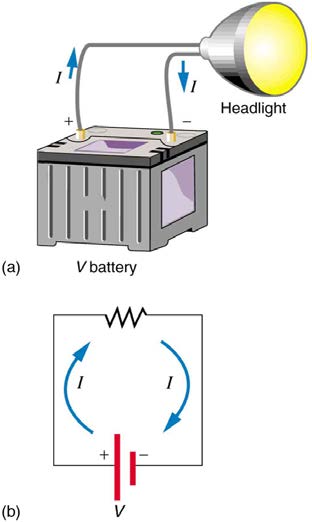
CHAPTER 20 | ELECTRIC CURRENT, RESISTANCE, AND OHM'S LAW 697
Example 20.1 Calculating Currents: Current in a Truck Battery and a Handheld Calculator
(a) What is the current involved when a truck battery sets in motion 720 C of charge in 4.00 s while starting an engine? (b) How long does it take
1.00 C of charge to flow through a handheld calculator if a 0.300-mA current is flowing?
Strategy
We can use the definition of current in the equation I = Δ Q / Δ t to find the current in part (a), since charge and time are given. In part (b), we
rearrange the definition of current and use the given values of charge and current to find the time required.
Solution for (a)
Entering the given values for charge and time into the definition of current gives
(20.3)
I = Δ Q
Δ t = 720 C
4.00 s = 180 C/s
= 180 A.
Discussion for (a)
This large value for current illustrates the fact that a large charge is moved in a small amount of time. The currents in these “starter motors” are
fairly large because large frictional forces need to be overcome when setting something in motion.
Solution for (b)
Solving the relationship I = Δ Q / Δ t for time Δ t , and entering the known values for charge and current gives
(20.4)
Δ t = Δ Q















