ambulance moving at 110 km/h and emitting a steady 800-Hz sound from
correspond to?
its siren? The speed of sound on this day is 345 m/s. (b) What frequency
does she receive after the ambulance has passed?
16. What sound intensity level in dB is produced by earphones that
31. (a) At an air show a jet flies directly toward the stands at a speed of
create an intensity of 4.00×10−2 W/m2 ?
1200 km/h, emitting a frequency of 3500 Hz, on a day when the speed of
sound is 342 m/s. What frequency is received by the observers? (b) What
17. Show that an intensity of 10–12 W/m2 is the same as
frequency do they receive as the plane flies directly away from them?
10–16 W/cm2 .
32. What frequency is received by a mouse just before being dispatched
18. (a) What is the decibel level of a sound that is twice as intense as a
by a hawk flying at it at 25.0 m/s and emitting a screech of frequency
90.0-dB sound? (b) What is the decibel level of a sound that is one-fifth
3500 Hz? Take the speed of sound to be 331 m/s.
as intense as a 90.0-dB sound?
33. A spectator at a parade receives an 888-Hz tone from an oncoming
trumpeter who is playing an 880-Hz note. At what speed is the musician
approaching if the speed of sound is 338 m/s?
624 CHAPTER 17 | PHYSICS OF HEARING
34. A commuter train blows its 200-Hz horn as it approaches a crossing.
51. Calculate the first overtone in an ear canal, which resonates like a
The speed of sound is 335 m/s. (a) An observer waiting at the crossing
2.40-cm-long tube closed at one end, by taking air temperature to be
receives a frequency of 208 Hz. What is the speed of the train? (b) What
37.0ºC . Is the ear particularly sensitive to such a frequency? (The
frequency does the observer receive as the train moves away?
resonances of the ear canal are complicated by its nonuniform shape,
35. Can you perceive the shift in frequency produced when you pull a
which we shall ignore.)
tuning fork toward you at 10.0 m/s on a day when the speed of sound is
52. A crude approximation of voice production is to consider the
344 m/s? To answer this question, calculate the factor by which the
breathing passages and mouth to be a resonating tube closed at one
frequency shifts and see if it is greater than 0.300%.
end. (See Figure 17.30.) (a) What is the fundamental frequency if the
36. Two eagles fly directly toward one another, the first at 15.0 m/s and
tube is 0.240-m long, by taking air temperature to be 37.0ºC ? (b) What
the second at 20.0 m/s. Both screech, the first one emitting a frequency
would this frequency become if the person replaced the air with helium?
of 3200 Hz and the second one emitting a frequency of 3800 Hz. What
Assume the same temperature dependence for helium as for air.
frequencies do they receive if the speed of sound is 330 m/s?
53. (a) Students in a physics lab are asked to find the length of an air
37. What is the minimum speed at which a source must travel toward you
column in a tube closed at one end that has a fundamental frequency of
for you to be able to hear that its frequency is Doppler shifted? That is,
256 Hz. They hold the tube vertically and fill it with water to the top, then
what speed produces a shift of 0.300% on a day when the speed of
lower the water while a 256-Hz tuning fork is rung and listen for the first
sound is 331 m/s?
resonance. What is the air temperature if the resonance occurs for a
length of 0.336 m? (b) At what length will they observe the second
17.5 Sound Interference and Resonance: Standing
resonance (first overtone)?
Waves in Air Columns
54. What frequencies will a 1.80-m-long tube produce in the audible
38. A “showy” custom-built car has two brass horns that are supposed to
range at 20.0ºC if: (a) The tube is closed at one end? (b) It is open at
produce the same frequency but actually emit 263.8 and 264.5 Hz. What
both ends?
beat frequency is produced?
39. What beat frequencies will be present: (a) If the musical notes A and
17.6 Hearing
C are played together (frequencies of 220 and 264 Hz)? (b) If D and F
are played together (frequencies of 297 and 352 Hz)? (c) If all four are
55. The factor of 10−12 in the range of intensities to which the ear can
played together?
respond, from threshold to that causing damage after brief exposure, is
truly remarkable. If you could measure distances over the same range
40. What beat frequencies result if a piano hammer hits three strings that
with a single instrument and the smallest distance you could measure
emit frequencies of 127.8, 128.1, and 128.3 Hz?
was 1 mm, what would the largest be?
41. A piano tuner hears a beat every 2.00 s when listening to a 264.0-Hz
tuning fork and a single piano string. What are the two possible
56. The frequencies to which the ear responds vary by a factor of 103 .
frequencies of the string?
Suppose the speedometer on your car measured speeds differing by the
42. (a) What is the fundamental frequency of a 0.672-m-long tube, open
same factor of 103 , and the greatest speed it reads is 90.0 mi/h. What
at both ends, on a day when the speed of sound is 344 m/s? (b) What is
would be the slowest nonzero speed it could read?
the frequency of its second harmonic?
57. What are the closest frequencies to 500 Hz that an average person
43. If a wind instrument, such as a tuba, has a fundamental frequency of
can clearly distinguish as being different in frequency from 500 Hz? The
32.0 Hz, what are its first three overtones? It is closed at one end. (The
sounds are not present simultaneously.
overtones of a real tuba are more complex than this example, because it
is a tapered tube.)
58. Can the average person tell that a 2002-Hz sound has a different
frequency than a 1999-Hz sound without playing them simultaneously?
44. What are the first three overtones of a bassoon that has a
fundamental frequency of 90.0 Hz? It is open at both ends. (The
59. If your radio is producing an average sound intensity level of 85 dB,
overtones of a real bassoon are more complex than this example,
what is the next lowest sound intensity level that is clearly less intense?
because its double reed makes it act more like a tube closed at one
60. Can you tell that your roommate turned up the sound on the TV if its
end.)
average sound intensity level goes from 70 to 73 dB?
45. How long must a flute be in order to have a fundamental frequency of
61. Based on the graph in Figure 17.36, what is the threshold of hearing
262 Hz (this frequency corresponds to middle C on the evenly tempered
in decibels for frequencies of 60, 400, 1000, 4000, and 15,000 Hz? Note
chromatic scale) on a day when air temperature is 20.0ºC ? It is open at that many AC electrical appliances produce 60 Hz, music is commonly
both ends.
400 Hz, a reference frequency is 1000 Hz, your maximum sensitivity is
near 4000 Hz, and many older TVs produce a 15,750 Hz whine.
46. What length should an oboe have to produce a fundamental
frequency of 110 Hz on a day when the speed of sound is 343 m/s? It is
62. What sound intensity levels must sounds of frequencies 60, 3000,
open at both ends.
and 8000 Hz have in order to have the same loudness as a 40-dB sound
of frequency 1000 Hz (that is, to have a loudness of 40 phons)?
47. What is the length of a tube that has a fundamental frequency of 176
Hz and a first overtone of 352 Hz if the speed of sound is 343 m/s?
63. What is the approximate sound intensity level in decibels of a 600-Hz
tone if it has a loudness of 20 phons? If it has a loudness of 70 phons?
48. (a) Find the length of an organ pipe closed at one end that produces
a fundamental frequency of 256 Hz when air temperature is 18.0ºC . (b) 64. (a) What are the loudnesses in phons of sounds having frequencies
of 200, 1000, 5000, and 10,000 Hz, if they are all at the same 60.0-dB
What is its fundamental frequency at 25.0ºC ?
sound intensity level? (b) If they are all at 110 dB? (c) If they are all at
49. By what fraction will the frequencies produced by a wind instrument
20.0 dB?
change when air temperature goes from 10.0ºC to 30.0ºC ? That is,
65. Suppose a person has a 50-dB hearing loss at all frequencies. By
find the ratio of the frequencies at those temperatures.
how many factors of 10 will low-intensity sounds need to be amplified to
seem normal to this person? Note that smaller amplification is
50. The ear canal resonates like a tube closed at one end. (See Figure
appropriate for more intense sounds to avoid further hearing damage.
17.39.) If ear canals range in length from 1.80 to 2.60 cm in an average
population, what is the range of fundamental resonant frequencies? Take
66. If a woman needs an amplification of 5.0×1012 times the threshold
air temperature to be 37.0ºC , which is the same as body temperature.
intensity to enable her to hear at all frequencies, what is her overall
How does this result correlate with the intensity versus frequency graph
hearing loss in dB? Note that smaller amplification is appropriate for more
(Figure 17.37 of the human ear?
CHAPTER 17 | PHYSICS OF HEARING 625
intense sounds to avoid further damage to her hearing from levels above
83. A dolphin is able to tell in the dark that the ultrasound echoes
90 dB.
received from two sharks come from two different objects only if the
67. (a) What is the intensity in watts per meter squared of a just barely
sharks are separated by 3.50 m, one being that much farther away than
audible 200-Hz sound? (b) What is the intensity in watts per meter
the other. (a) If the ultrasound has a frequency of 100 kHz, show this
squared of a barely audible 4000-Hz sound?
ability is not limited by its wavelength. (b) If this ability is due to the
dolphin’s ability to detect the arrival times of echoes, what is the minimum
68. (a) Find the intensity in watts per meter squared of a 60.0-Hz sound
time difference the dolphin can perceive?
having a loudness of 60 phons. (b) Find the intensity in watts per meter
squared of a 10,000-Hz sound having a loudness of 60 phons.
84. A diagnostic ultrasound echo is reflected from moving blood and
returns with a frequency 500 Hz higher than its original 2.00 MHz. What
69. A person has a hearing threshold 10 dB above normal at 100 Hz and
is the velocity of the blood? (Assume that the frequency of 2.00 MHz is
50 dB above normal at 4000 Hz. How much more intense must a 100-Hz
accurate to seven significant figures and 500 Hz is accurate to three
tone be than a 4000-Hz tone if they are both barely audible to this
significant figures.)
person?
85. Ultrasound reflected from an oncoming bloodstream that is moving at
70. A child has a hearing loss of 60 dB near 5000 Hz, due to noise
30.0 cm/s is mixed with the original frequency of 2.50 MHz to produce
exposure, and normal hearing elsewhere. How much more intense is a
beats. What is the beat frequency? (Assume that the frequency of 2.50
5000-Hz tone than a 400-Hz tone if they are both barely audible to the
MHz is accurate to seven significant figures.)
child?
71. What is the ratio of intensities of two sounds of identical frequency if
the first is just barely discernible as louder to a person than the second?
17.7 Ultrasound
72. Unless otherwise indicated, for problems in this section, assume
that the speed of sound through human tissues is 1540 m/s.
73. What is the sound intensity level in decibels of ultrasound of intensity
105 W/m2 , used to pulverize tissue during surgery?
74. Is 155-dB ultrasound in the range of intensities used for deep
heating? Calculate the intensity of this ultrasound and compare this
intensity with values quoted in the text.
75. Find the sound intensity level in decibels of 2.00×10–2 W/m2
ultrasound used in medical diagnostics.
76. The time delay between transmission and the arrival of the reflected
wave of a signal using ultrasound traveling through a piece of fat tissue
was 0.13 ms. At what depth did this reflection occur?
77. In the clinical use of ultrasound, transducers are always coupled to
the skin by a thin layer of gel or oil, replacing the air that would otherwise
exist between the transducer and the skin. (a) Using the values of
acoustic impedance given in Table 17.5 calculate the intensity reflection
coefficient between transducer material and air. (b) Calculate the intensity
reflection coefficient between transducer material and gel (assuming for
this problem that its acoustic impedance is identical to that of water). (c)
Based on the results of your calculations, explain why the gel is used.
78. (a) Calculate the minimum frequency of ultrasound that will allow you
to see details as small as 0.250 mm in human tissue. (b) What is the
effective depth to which this sound is effective as a diagnostic probe?
79. (a) Find the size of the smallest detail observable in human tissue
with 20.0-MHz ultrasound. (b) Is its effective penetration depth great
enough to examine the entire eye (about 3.00 cm is needed)? (c) What is
the wavelength of such ultrasound in 0ºC air?
80. (a) Echo times are measured by diagnostic ultrasound scanners to
determine distances to reflecting surfaces in a patient. What is the
difference in echo times for tissues that are 3.50 and 3.60 cm beneath
the surface? (This difference is the minimum resolving time for the
scanner to see details as small as 0.100 cm, or 1.00 mm. Discrimination
of smaller time differences is needed to see smaller details.) (b) Discuss
whether the period T of this ultrasound must be smaller than the
minimum time resolution. If so, what is the minimum frequency of the
ultrasound and is that out of the normal range for diagnostic ultrasound?
81. (a) How far apart are two layers of tissue that produce echoes having
round-trip times (used to measure distances) that differ by 0.750 μs ?
(b) What minimum frequency must the ultrasound have to see detail this
small?
82. (a) A bat uses ultrasound to find its way among trees. If this bat can
detect echoes 1.00 ms apart, what minimum distance between objects
can it detect? (b) Could this distance explain the difficulty that bats have
finding an open door when they accidentally get into a house?
626 CHAPTER 17 | PHYSICS OF HEARING

CHAPTER 18 | ELECTRIC CHARGE AND ELECTRIC FIELD 627
18
ELECTRIC CHARGE AND ELECTRIC FIELD
Figure 18.1 Static electricity from this plastic slide causes the child’s hair to stand on end. The sliding motion stripped electrons away from the child’s body, leaving an excess of positive charges, which repel each other along each strand of hair. (credit: Ken Bosma/Wikimedia Commons)
Learning Objectives
18.1. Static Electricity and Charge: Conservation of Charge
• Define electric charge, and describe how the two types of charge interact.
• Describe three common situations that generate static electricity.
• State the law of conservation of charge.
18.2. Conductors and Insulators
• Define conductor and insulator, explain the difference, and give examples of each.
• Describe three methods for charging an object.
• Explain what happens to an electric force as you move farther from the source.
• Define polarization.
18.3. Coulomb’s Law
• State Coulomb’s law in terms of how the electrostatic force changes with the distance between two objects.
• Calculate the electrostatic force between two charged point forces, such as electrons or protons.
• Compare the electrostatic force to the gravitational attraction for a proton and an electron; for a human and the Earth.
18.4. Electric Field: Concept of a Field Revisited
• Describe a force field and calculate the strength of an electric field due to a point charge.
• Calculate the force exerted on a test charge by an electric field.
• Explain the relationship between electrical force (F) on a test charge and electrical field strength (E).
18.5. Electric Field Lines: Multiple Charges
• Calculate the total force (magnitude and direction) exerted on a test charge from more than one charge
• Describe an electric field diagram of a positive point charge; of a negative point charge with twice the magnitude of positive charge
• Draw the electric field lines between two points of the same charge; between two points of opposite charge.
18.6. Electric Forces in Biology
• Describe how a water molecule is polar.
• Explain electrostatic screening by a water molecule within a living cell.
18.7. Conductors and Electric Fields in Static Equilibrium
• List the three properties of a conductor in electrostatic equilibrium.
• Explain the effect of an electric field on free charges in a conductor.
• Explain why no electric field may exist inside a conductor.
• Describe the electric field surrounding Earth.
• Explain what happens to an electric field applied to an irregular conductor.
• Describe how a lightning rod works.
• Explain how a metal car may protect passengers inside from the dangerous electric fields caused by a downed line touching the car.
18.8. Applications of Electrostatics
• Name several real-world applications of the study of electrostatics.
628 CHAPTER 18 | ELECTRIC CHARGE AND ELECTRIC FIELD
Introduction to Electric Charge and Electric Field
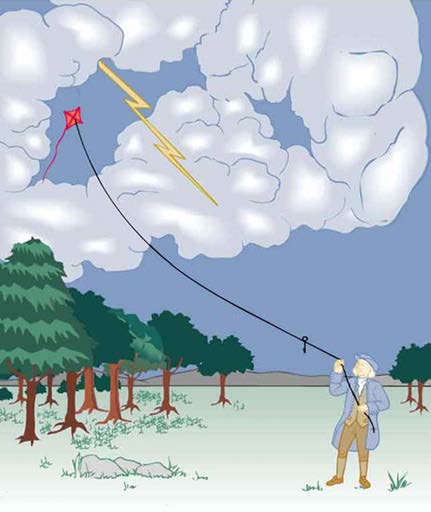
The image of American politician and scientist Benjamin Franklin (1706–1790) flying a kite in a thunderstorm is familiar to every schoolchild. (See
Figure 18.2.) In this experiment, Franklin demonstrated a connection between lightning and static electricity. Sparks were drawn from a key hung on a kite string during an electrical storm. These sparks were like those produced by static electricity, such as the spark that jumps from your finger to
a metal doorknob after you walk across a wool carpet. What Franklin demonstrated in his dangerous experiment was a connection between
phenomena on two different scales: one the grand power of an electrical storm, the other an effect of more human proportions. Connections like this
one reveal the underlying unity of the laws of nature, an aspect we humans find particularly appealing.
Figure 18.2 When Benjamin Franklin demonstrated that lightning was related to static electricity, he made a connection that is now part of the evidence that all directly
experienced forces except the gravitational force are manifestations of the electromagnetic force.
Much has been written about Franklin. His experiments were only part of the life of a man who was a scientist, inventor, revolutionary, statesman, and
writer. Franklin’s experiments were not performed in isolation, nor were they the only ones to reveal connections.
For example, the Italian scientist Luigi Galvani (1737–1798) performed a series of experiments in which static electricity was used to stimulate
contractions of leg muscles of dead frogs, an effect already known in humans subjected to static discharges. But Galvani also found that if he joined
two metal wires (say copper and zinc) end to end and touched the other ends to muscles, he produced the same effect in frogs as static discharge.
Alessandro Volta (1745–1827), partly inspired by Galvani’s work, experimented with various combinations of metals and developed the battery.
During the same era, other scientists made progress in discovering fundamental connections. The periodic table was developed as the systematic
properties of the elements were discovered. This influenced the development and refinement of the concept of atoms as the basis of matter. Such
submicroscopic descriptions of matter also help explain a great deal more.
Atomic and molecular interactions, such as the forces of friction, cohesion, and adhesion, are now known to be manifestations of the
electromagnetic force. Static electricity is just one aspect of the electromagnetic force, which also includes moving electricity and magnetism.
All the macroscopic forces that we experience directly, such as the sensations of touch and the tension in a rope, are due to the electromagnetic
force, one of the four fundamental forces in nature. The gravitational force, another fundamental force, is actually sensed through the electromagnetic
interaction of molecules, such as between those in our feet and those on the top of a bathroom scale. (The other two fundamental forces, the strong
nuclear force and the weak nuclear force, cannot be sensed on the human scale.)
This chapter begins the study of electromagnetic phenomena at a fundamental level. The next several chapters will cover static electricity, moving
electricity, and magnetism—collectively known as electromagnetism. In this chapter, we begin with the study of electric phenomena due to charges
that are at least temporarily stationary, called electrostatics, or static electricity.

CHAPTER 18 | ELECTRIC CHARGE AND ELECTRIC FIELD 629
18.1 Static Electricity and Charge: Conservation of Charge
Figure 18.3 Borneo amber was mined in Sabah, Malaysia, from shale-sandstone-mudstone veins. When a piece of amber is rubbed with a piece of silk, the amber gains more
electrons, giving it a net negative charge. At the same time, the silk, having lost electrons, becomes positively charged. (credit: Sebakoamber, Wikimedia Commons)
What makes plastic wrap cling? Static electricity. Not only are applications of static electricity common these days, its existence has been known
since ancient times. The first record of its effects dates to ancient Greeks who noted more than 500 years B.C. that polishing amber temporarily
enabled it to attract bits of straw (see Figure 18.3). The very word electric derives from the Greek word for amber ( electron).
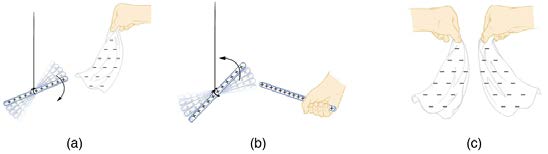
Many of the characteristics of static electricity can be explored by rubbing things together. Rubbing creates the spark you get from walking across a
wool carpet, for example. Static cling generated in a clothes dryer and the attraction of straw to recently polished amber also result from rubbing.
Similarly, lightning results from air movements under certain weather conditions. You can also rub a balloon on your hair, and the static electricity
created can then make the balloon cling to a wall. We also have to be cautious of static electricity, especia







