source and the observer are both in motion.
Check Your Understanding
Describe a situation in your life when you might rely on the Doppler shift to help you either while driving a car or walking near traffic.
Solution
If I am driving and I hear Doppler shift in an ambulance siren, I would be able to tell when it was getting closer and also if it has passed by. This
would help me to know whether I needed to pull over and let the ambulance through.

CHAPTER 17 | PHYSICS OF HEARING 603
17.5 Sound Interference and Resonance: Standing Waves in Air Columns
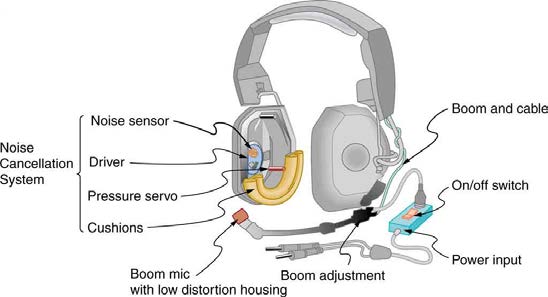
Figure 17.21 Some types of headphones use the phenomena of constructive and destructive interference to cancel out outside noises. (credit: JVC America, Flickr)
Interference is the hallmark of waves, all of which exhibit constructive and destructive interference exactly analogous to that seen for water waves. In
fact, one way to prove something “is a wave” is to observe interference effects. So, sound being a wave, we expect it to exhibit interference; we have
already mentioned a few such effects, such as the beats from two similar notes played simultaneously.
Figure 17.22 shows a clever use of sound interference to cancel noise. Larger-scale applications of active noise reduction by destructive interference are contemplated for entire passenger compartments in commercial aircraft. To obtain destructive interference, a fast electronic analysis is
performed, and a second sound is introduced with its maxima and minima exactly reversed from the incoming noise. Sound waves in fluids are
pressure waves and consistent with Pascal’s principle; pressures from two different sources add and subtract like simple numbers; that is, positive
and negative gauge pressures add to a much smaller pressure, producing a lower-intensity sound. Although completely destructive interference is
possible only under the simplest conditions, it is possible to reduce noise levels by 30 dB or more using this technique.
Figure 17.22 Headphones designed to cancel noise with destructive interference create a sound wave exactly opposite to the incoming sound. These headphones can be
more effective than the simple passive attenuation used in most ear protection. Such headphones were used on the record-setting, around the world nonstop flight of the
Voyager aircraft to protect the pilots’ hearing from engine noise.
Where else can we observe sound interference? All sound resonances, such as in musical instruments, are due to constructive and destructive
interference. Only the resonant frequencies interfere constructively to form standing waves, while others interfere destructively and are absent. From
the toot made by blowing over a bottle, to the characteristic flavor of a violin’s sounding box, to the recognizability of a great singer’s voice, resonance
and standing waves play a vital role.
Interference
Interference is such a fundamental aspect of waves that observing interference is proof that something is a wave. The wave nature of light was
established by experiments showing interference. Similarly, when electrons scattered from crystals exhibited interference, their wave nature was
confirmed to be exactly as predicted by symmetry with certain wave characteristics of light.
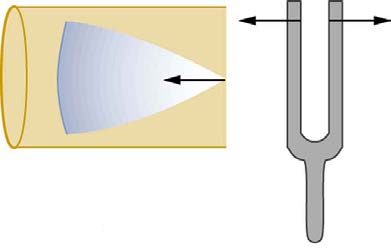
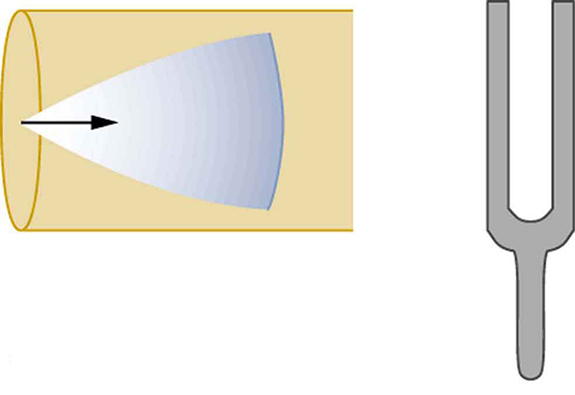
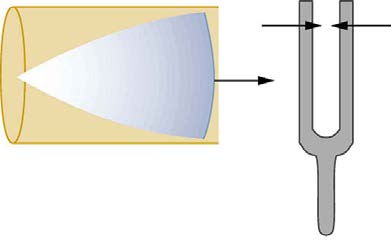
Suppose we hold a tuning fork near the end of a tube that is closed at the other end, as shown in Figure 17.23, Figure 17.24, Figure 17.25, and
Figure 17.26. If the tuning fork has just the right frequency, the air column in the tube resonates loudly, but at most frequencies it vibrates very little.
This observation just means that the air column has only certain natural frequencies. The figures show how a resonance at the lowest of these
natural frequencies is formed. A disturbance travels down the tube at the speed of sound and bounces off the closed end. If the tube is just the right
length, the reflected sound arrives back at the tuning fork exactly half a cycle later, and it interferes constructively with the continuing sound produced
by the tuning fork. The incoming and reflected sounds form a standing wave in the tube as shown.
604 CHAPTER 17 | PHYSICS OF HEARING
Figure 17.23 Resonance of air in a tube closed at one end, caused by a tuning fork. A disturbance moves down the tube.
Figure 17.24 Resonance of air in a tube closed at one end, caused by a tuning fork. The disturbance reflects from the closed end of the tube.
Figure 17.25 Resonance of air in a tube closed at one end, caused by a tuning fork. If the length of the tube L is just right, the disturbance gets back to the tuning fork half a cycle later and interferes constructively with the continuing sound from the tuning fork. This interference forms a standing wave, and the air column resonates.
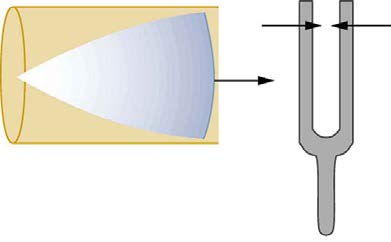
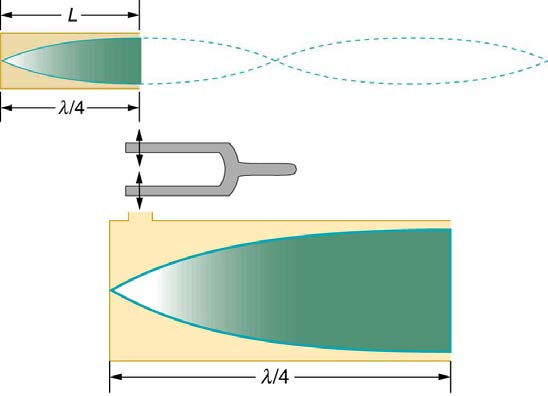
Figure 17.26 Resonance of air in a tube closed at one end, caused by a tuning fork. A graph of air displacement along the length of the tube shows none at the closed end,
where the motion is constrained, and a maximum at the open end. This standing wave has one-fourth of its wavelength in the tube, so that λ = 4 L .
The standing wave formed in the tube has its maximum air displacement (an antinode) at the open end, where motion is unconstrained, and no
displacement (a node) at the closed end, where air movement is halted. The distance from a node to an antinode is one-fourth of a wavelength, and
this equals the length of the tube; thus, λ = 4 L . This same resonance can be produced by a vibration introduced at or near the closed end of the
tube, as shown in Figure 17.27. It is best to consider this a natural vibration of the air column independently of how it is induced.
CHAPTER 17 | PHYSICS OF HEARING 605
Figure 17.27 The same standing wave is created in the tube by a vibration introduced near its closed end.
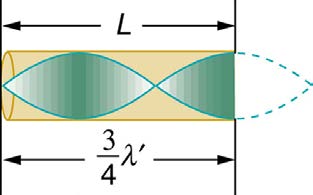
Given that maximum air displacements are possible at the open end and none at the closed end, there are other, shorter wavelengths that can
resonate in the tube, such as the one shown in Figure 17.28. Here the standing wave has three-fourths of its wavelength in the tube, or
L = (3 / 4) λ′ , so that λ′ = 4 L / 3 . Continuing this process reveals a whole series of shorter-wavelength and higher-frequency sounds that
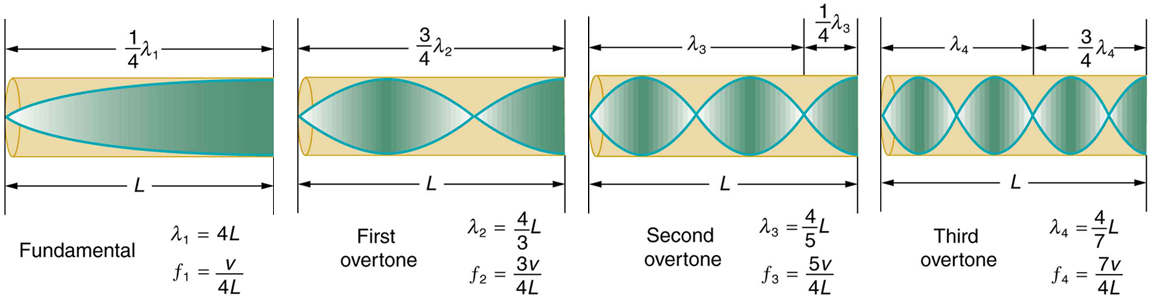
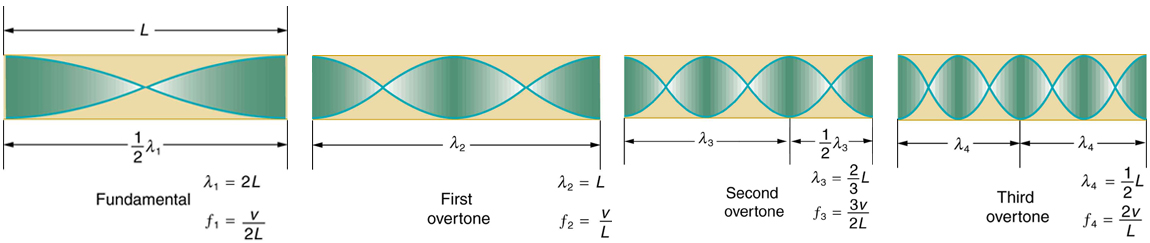
resonate in the tube. We use specific terms for the resonances in any system. The lowest resonant frequency is called the fundamental, while all
higher resonant frequencies are called overtones. All resonant frequencies are integral multiples of the fundamental, and they are collectively called
harmonics. The fundamental is the first harmonic, the first overtone is the second harmonic, and so on. Figure 17.29 shows the fundamental and the first three overtones (the first four harmonics) in a tube closed at one end.
Figure 17.28 Another resonance for a tube closed at one end. This has maximum air displacements at the open end, and none at the closed end. The wavelength is shorter,
with three-fourths λ′ equaling the length of the tube, so that λ′ = 4 L / 3 . This higher-frequency vibration is the first overtone.
Figure 17.29 The fundamental and three lowest overtones for a tube closed at one end. All have maximum air displacements at the open end and none at the closed end.
The fundamental and overtones can be present simultaneously in a variety of combinations. For example, middle C on a trumpet has a sound
distinctively different from middle C on a clarinet, both instruments being modified versions of a tube closed at one end. The fundamental frequency is
the same (and usually the most intense), but the overtones and their mix of intensities are different and subject to shading by the musician. This mix
is what gives various musical instruments (and human voices) their distinctive characteristics, whether they have air columns, strings, sounding
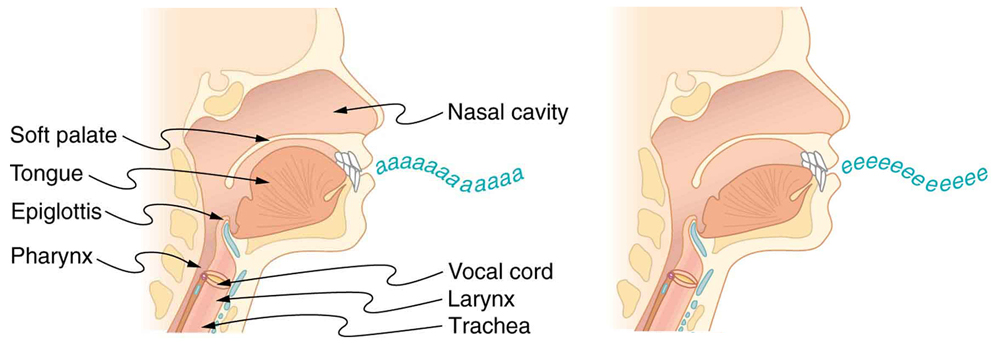
boxes, or drumheads. In fact, much of our speech is determined by shaping the cavity formed by the throat and mouth and positioning the tongue to
adjust the fundamental and combination of overtones. Simple resonant cavities can be made to resonate with the sound of the vowels, for example.
(See Figure 17.30.) In boys, at puberty, the larynx grows and the shape of the resonant cavity changes giving rise to the difference in predominant frequencies in speech between men and women.
606 CHAPTER 17 | PHYSICS OF HEARING
Figure 17.30 The throat and mouth form an air column closed at one end that resonates in response to vibrations in the voice box. The spectrum of overtones and their
intensities vary with mouth shaping and tongue position to form different sounds. The voice box can be replaced with a mechanical vibrator, and understandable speech is still
possible. Variations in basic shapes make different voices recognizable.
Now let us look for a pattern in the resonant frequencies for a simple tube that is closed at one end. The fundamental has λ = 4 L , and frequency is
related to wavelength and the speed of sound as given by:
v
(17.28)
w = fλ.
Solving for f in this equation gives
(17.29)
f = v w
λ = v w
4 L,
where v w is the speed of sound in air. Similarly, the first overtone has λ′ = 4 L / 3 (see Figure 17.29), so that
(17.30)
f ′ = 3 v w
4 L = 3 f .
Because f ′ = 3 f , we call the first overtone the third harmonic. Continuing this process, we see a pattern that can be generalized in a single
expression. The resonant frequencies of a tube closed at one end are
(17.31)
fn = nv w
4 L, n = 1,3,5,
where f 1 is the fundamental, f 3 is the first overtone, and so on. It is interesting that the resonant frequencies depend on the speed of sound and,
hence, on temperature. This dependence poses a noticeable problem for organs in old unheated cathedrals, and it is also the reason why musicians
commonly bring their wind instruments to room temperature before playing them.
Example 17.5 Find the Length of a Tube with a 128 Hz Fundamental
(a) What length should a tube closed at one end have on a day when the air temperature, is 22.0ºC , if its fundamental frequency is to be 128
Hz (C below middle C)?
(b) What is the frequency of its fourth overtone?
Strategy
The length L can be found from the relationship in fn = nv w
4 L , but we will first need to find the speed of sound v w .
Solution for (a)
(1) Identify knowns:
• the fundamental frequency is 128 Hz
• the air temperature is 22.0ºC
(2) Use fn = nv w
4 L to find the fundamental frequency ( n = 1 ).
(17.32)
f 1 = v w
4 L
(3) Solve this equation for length.
(17.33)
L = v w
4 f 1
(4) Find the speed of sound using v w = (331 m/s)
T
273 K .
(17.34)
v w = (331 m/s) 295 K
273 K = 344 m/s
(5) Enter the values of the speed of sound and frequency into the expression for L .
CHAPTER 17 | PHYSICS OF HEARING 607
(17.35)
L = v w
4 f = 344 m/s
1
4(128 Hz) = 0.672 m
Discussion on (a)
Many wind instruments are modified tubes that have finger holes, valves, and other devices for changing the length of the resonating air column
and hence, the frequency of the note played. Horns producing very low frequencies, such as tubas, require tubes so long that they are coiled into
loops.
Solution for (b)
(1) Identify knowns:
• the first overtone has n = 3
• the second overtone has n = 5
• the third overtone has n = 7
• the fourth overtone has n = 9
(2) Enter the value for the fourth overtone into fn = nv w
4 L .
(17.36)
f 9 = 9 v w
4 L = 9 f 1 = 1.15 kHz
Discussion on (b)
Whether this overtone occurs in a simple tube or a musical instrument depends on how it is stimulated to vibrate and the details of its shape. The
trombone, for example, does not produce its fundamental frequency and only makes overtones.
Another type of tube is one that is open at both ends. Examples are some organ pipes, flutes, and oboes. The resonances of tubes open at both
ends can be analyzed in a very similar fashion to those for tubes closed at one end. The air columns in tubes open at both ends have maximum air
displacements at both ends, as illustrated in Figure 17.31. Standing waves form as shown.
Figure 17.31 The resonant frequencies of a tube open at both ends are shown, including the fundamental and the first three overtones. In all cases the maximum air
displacements occur at both ends of the tube, giving it different natural frequencies than a tube closed at one end.
Based on the fact that a tube open at both ends has maximum air displacements at both ends, and using Figure 17.31 as a guide, we can see that
the resonant frequencies of a tube open at both ends are:
(17.37)
fn = nv w
2 L, n = 1, 2, 3...,
where f 1 is the fundamental, f 2 is the first overtone, f 3 is the second overtone, and so on. Note that a tube open at both ends has a fundamental
frequency twice what it would have if closed at one end. It also has a different spectrum of overtones than a tube closed at one end. So if you had two
tubes with the same fundamental frequency but one was open at both ends and the other was closed at one end, they would sound different when
played because they have different overtones. Middle C, for example, would sound richer played on an open tube, because it has even multiples of
the fundamental as well as odd. A closed tube has only odd multiples.
Real-World Applications: Resonance in Everyday Systems
Resonance occurs in many different systems, including strings, air columns, and atoms. Resonance is the driven or forced oscillation of a system
at its natural frequency. At resonance, energy is transferred rapidly to the oscillating system, and the amplitude of its oscillations grows until the
system can no longer be described by Hooke’s law. An example of this is the distorted sound intentionally produced in certain types of rock
music.
Wind instruments use resonance in air columns to amplify tones made by lips or vibrating reeds. Other instruments also use air resonance in clever
ways to amplify sound. Figure 17.32 shows a violin and a guitar, both of which have sounding boxes but with different shapes, resulting in different overtone structures. The vibrating string creates a sound that resonates in the sounding box, greatly amplifying the sound and creating overtones that
give the instrument its characteristic flavor. The more complex the shape of the sounding box, the greater its ability to resonate over a wide range of
frequencies. The marimba, like the one shown in Figure 17.33 uses pots or gourds below the wooden slats to amplify their tones. The resonance of
the pot can be adjusted by adding water.


608 CHAPTER 17 | PHYSICS OF HEARING
Figure 17.32 String instruments such as violins and guitars use resonance in their sounding boxes to amplify and enrich the sound created by their vibrating strings. The
bridge and supports couple the string vibrations to the sounding boxes and air within. (credits: guitar, Feliciano Guimares, Fotopedia; violin, Steve Snodgrass, Flickr)
Figure 17.33 Resonance has been used in musical instruments since prehistoric times. This marimba uses gourds as resonance chambers to amplify its sound. (credit: APC
Events, Flickr)
We have emphasized sound applications in our discussions of resonance and standing waves, but these ideas apply to any system that has wave
characteristics. Vibrating strings, for example, are actually resonating and have fundamentals and overtones similar to those for air columns. More
subtle are the resonances in atoms due to the wave character of their electrons. Their orbitals can be viewed as standing waves, which have a
fundamental (ground state) and overtones (excited states). It is fascinating that wave characteristics apply to such a wide range of physical systems.
Check Your Understanding
Describe how noise-canceling headphones differ from standard headphones used to block outside sounds.
Solution
Regular headphones only block sound waves with a physical barrier. Noise-canceling headphones use destructive interference to reduce the
loudness of outside sounds.
Check Your Understanding
How is it possible to use a standing wave's node and antinode to determine the length of a closed-end tube?
Solution
When the tube resonates at its natural frequency, the wave's node is located at the closed end of the tube, and the antinode is located at the
open end. The length of the tube is equal to one-fourth of the wavelength of this wave. Thus, if we know the wavelength of the wave, we can
determine the length of the tube.


CHAPTER 17 | PHYSICS OF HEARING 609
PhET Explorations: Sound
This simulation lets you see sound waves. Adjust the frequency or volume and you can see and hear how the wave changes. Move the listener
around and hear what she hears.
Figure 17.34 Sound (http://cnx.org/content/m42296/1.4/sound_en.jar)
17.6 Hearing
Figure 17.35 Hearing allows this vocalist, his band, and his fans to enjoy music. (credit: West Point Public Affairs, Flickr)
The human ear has a tremendous range and sensitivity. It can give us a wealth of simple information—such as pitch, loudness, and direction. And
from its input we can detect musical quality and nuances of voiced emotion. How is our hearing related to the physical qualities of sound, and how
does the hearing mechanism work?
Hearing is the perception of sound. (Perception is commonly defined to be awareness through the senses, a typically circular definition of higher-
level processes in living organisms.) Normal human hearing encompasses frequencies from 20 to 20,000 Hz, an impressive range. Sounds below 20
Hz are called infrasound, whereas those above 20,000 Hz are ultrasound. Neither is perceived by the ear, although infrasound can sometimes be
felt as vibrations. When we do hear low-frequency vibrations, such as the sounds of a diving board, we hear the individual vibrations only because
there are higher-frequency sounds in each. Other animals have hearing ranges different from that of humans. Dogs can hear sounds as high as
30,000 Hz, whereas bats and dolphins can hear up to 100,000-Hz sounds. You may have noticed that dogs respond to the sound of a dog whistle
which produces sound out of the range of human hearing. Elephants are known to respond to frequencies below 20 Hz.
The perception of frequency is called pitch. Most of us have excellent relative pitch, which means that we can tell whether one sound has a different
frequency from another. Typically, we can discriminate between two sounds if their frequencies differ by 0.3% or more. For example, 500.0 and 501.5
Hz are noticeably different. Pitch perception is directly related to frequency and is not greatly affected by other physical quantities such as intensity.
Musical notes are particular sounds that can be produced by most instruments and in Western music have particular names. Combinations of notes
constitute music. Some people can identify musical notes, such as A-sharp, C, or E-flat, just by listening to them. This uncommon ability is called
perfect pitch.
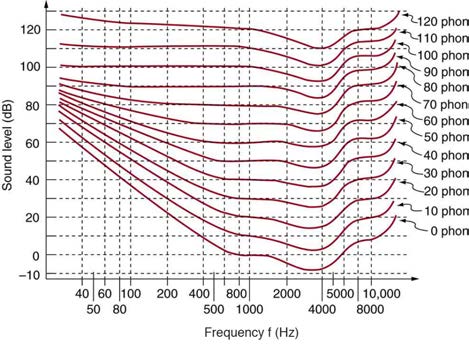
The ear is remarkably sensitive to low-intensity sounds. The lowest audible intensity or threshold is about 10−12 W/m2 or 0 dB. Sounds as much
as 1012 more intense can be briefly tolerated. Very few measuring devices are capable of observations over a range of a trillion. The perception of
intensity is called loudness. At a given frequency, it is possible to discern differences of about 1 dB, and a change of 3 dB is easily noticed. But
loudness is not related to intensity alone. Frequency has a major effect on how loud a sound seems. The ear has its maximum sensitivity to
frequencies in the range of 2000 to 5000 Hz, so that sounds in this range are perceived as being louder than, say, those at 500 or 10,000 Hz, even
when they all have the same intensity. Sounds near the high- and low-frequency extremes of the hearing range seem even less loud, because the
ear is even less sensitive at those frequencies. Table 17.4 gives the dependence of certain human hearing perceptions on physical quantities.
Table 17.4 Sound Perceptions
Perception
Physical quantity
Pitch
Frequency
Loudness
Intensity and Frequency
Number and relative intensity of multiple frequencies.
Timbre
Subtle craftsmanship leads to non-linear effects and more detail.
Note
Basic unit of music with specific names, combined to generate tunes
Tone
Number and relative intensity of multiple frequencies.
When a violin plays middle C, there is no mistaking it for a piano playing the same note. The reason is that each instrument produces a distinctive set
of frequencies and intensities. We call our perception of these combinations of frequencies and intensities tone quality, or more commonly the timbre
of the sound. It is more difficult to correlate timbre perception to physical quantities than it is for loudness or pitch perception. Timbre is more
subjective. Terms such as dull, brilliant, warm, cold, pure, and rich are employed to describe the timbre of a sound. So the consideration of timbre
610 CHAPTER 17 | PHYSICS OF HEARING
takes us into the realm of perceptual psychology, where higher-level processes in the brain are dominant. This is true for other perceptions of sound,
such as music and noise. We shall not delve further into them; rather, we will concentrate on the question of loud



















