door frame by a spring constant.
makes a single vibration as the tire moves. What is the frequency of
these vibrations if the car moves at 30.0 m/s?
(a) If the spring stretches 0.250 m while supporting an 8.0-kg child, what
is its spring constant?
12. Engineering Application
(b) What is the time for one complete bounce of this child? (c) What is the
Each piston of an engine makes a sharp sound every other revolution of
child’s maximum velocity if the amplitude of her bounce is 0.200 m?
the engine. (a) How fast is a race car going if its eight-cylinder engine
emits a sound of frequency 750 Hz, given that the engine makes 2000
21. A 90.0-kg skydiver hanging from a parachute bounces up and down
revolutions per kilometer? (b) At how many revolutions per minute is the
with a period of 1.50 s. What is the new period of oscillation when a
engine rotating?
second skydiver, whose mass is 60.0 kg, hangs from the legs of the first,
as seen in Figure 16.47.
16.3 Simple Harmonic Motion: A Special Periodic
Motion
13. A type of cuckoo clock keeps time by having a mass bouncing on a
spring, usually something cute like a cherub in a chair. What force
constant is needed to produce a period of 0.500 s for a 0.0150-kg mass?
14. If the spring constant of a simple harmonic oscillator is doubled, by
what factor will the mass of the system need to change in order for the
frequency of the motion to remain the same?

CHAPTER 16 | OSCILLATORY MOTION AND WAVES 585
16.5 Energy and the Simple Harmonic Oscillator
35. The length of nylon rope from which a mountain climber is suspended
has a force constant of 1.40×104 N/m .
(a) What is the frequency at which he bounces, given his mass plus and
the mass of his equipment are 90.0 kg?
(b) How much would this rope stretch to break the climber’s fall if he free-
falls 2.00 m before the rope runs out of slack? Hint: Use conservation of
energy.
(c) Repeat both parts of this problem in the situation where twice this
length of nylon rope is used.
36. Engineering Application
Near the top of the Citigroup Center building in New York City, there is an
Figure 16.47 The oscillations of one skydiver are about to be affected by a second
object with mass of 4.00×105 kg on springs that have adjustable force
skydiver. (credit: U.S. Army, www.army.mil)
constants. Its function is to dampen wind-driven oscillations of the
16.4 The Simple Pendulum
building by oscillating at the same frequency as the building is being
driven—the driving force is transferred to the object, which oscillates
As usual, the acceleration due to gravity in these problems is taken
instead of the entire building. (a) What effective force constant should the
to be g = 9.80 m / s2 , unless otherwise specified.
springs have to make the object oscillate with a period of 2.00 s? (b)
What energy is stored in the springs for a 2.00-m displacement from
22. What is the length of a pendulum that has a period of 0.500 s?
equilibrium?
23. Some people think a pendulum with a period of 1.00 s can be driven
with “mental energy” or psycho kinetically, because its period is the same
16.6 Uniform Circular Motion and Simple Harmonic
as an average heartbeat. True or not, what is the length of such a
Motion
pendulum?
37. (a)What is the maximum velocity of an 85.0-kg person bouncing on a
24. What is the period of a 1.00-m-long pendulum?
bathroom scale having a force constant of 1.50×106 N/m , if the
25. How long does it take a child on a swing to complete one swing if her
center of gravity is 4.00 m below the pivot?
amplitude of the bounce is 0.200 cm? (b)What is the maximum energy
stored in the spring?
26. The pendulum on a cuckoo clock is 5.00 cm long. What is its
frequency?
38. A novelty clock has a 0.0100-kg mass object bouncing on a spring
that has a force constant of 1.25 N/m. What is the maximum velocity of
27. Two parakeets sit on a swing with their combined center of mass 10.0 the object if the object bounces 3.00 cm above and below its equilibrium
cm below the pivot. At what frequency do they swing?
position? (b) How many joules of kinetic energy does the object have at
28. (a) A pendulum with that has a period of 3.00000 s and that is located its maximum velocity?
where the acceleration due to gravity is 9.79 m/s2 is moved to a
39. At what positions is the speed of a simple harmonic oscillator half its
maximum? That is, what values of x / X give v = ± v max / 2 , where X
location where it the acceleration due to gravity is 9.82 m/s2 . What is its is the amplitude of the motion?
new period? (b) Explain why so many digits are needed in the value for
the period, based on the relation between the period and the acceleration
40. A ladybug sits 12.0 cm from the center of a Beatles music album
due to gravity.
spinning at 33.33 rpm. What is the maximum velocity of its shadow on
the wall behind the turntable, if illuminated parallel to the record by the
29. A pendulum with a period of 2.00000 s in one location
parallel rays of the setting Sun?
⎛⎝ g = 9.80 m/s2⎞⎠ is moved to a new location where the period is now
16.7 Damped Harmonic Motion
1.99796 s. What is the acceleration due to gravity at its new location?
30. (a) What is the effect on the period of a pendulum if you double its
41. The amplitude of a lightly damped oscillator decreases by 3.0%
length?
during each cycle. What percentage of the mechanical energy of the
oscillator is lost in each cycle?
(b) What is the effect on the period of a pendulum if you decrease its
length by 5.00%?
16.8 Forced Oscillations and Resonance
31. Find the ratio of the new/old periods of a pendulum if the pendulum
42. How much energy must the shock absorbers of a 1200-kg car
were transported from Earth to the Moon, where the acceleration due to
dissipate in order to damp a bounce that initially has a velocity of 0.800
gravity is 1.63 m/s2 .
m/s at the equilibrium position? Assume the car returns to its original
vertical position.
32. At what rate will a pendulum clock run on the Moon, where the
43. If a car has a suspension system with a force constant of
acceleration due to gravity is 1.63 m/s2 , if it keeps time accurately on
Earth? That is, find the time (in hours) it takes the clock’s hour hand to
5.00×104 N/m , how much energy must the car’s shocks remove to
make one revolution on the Moon.
dampen an oscillation starting with a maximum displacement of 0.0750
m?
33. Suppose the length of a clock’s pendulum is changed by 1.000%,
exactly at noon one day. What time will it read 24.00 hours later,
44. (a) How much will a spring that has a force constant of 40.0 N/m be
assuming it the pendulum has kept perfect time before the change? Note
stretched by an object with a mass of 0.500 kg when hung motionless
that there are two answers, and perform the calculation to four-digit
from the spring? (b) Calculate the decrease in gravitational potential
precision.
energy of the 0.500-kg object when it descends this distance. (c) Part of
this gravitational energy goes into the spring. Calculate the energy stored
34. If a pendulum-driven clock gains 5.00 s/day, what fractional change in in the spring by this stretch, and compare it with the gravitational potential
pendulum length must be made for it to keep perfect time?
energy. Explain where the rest of the energy might go.

586 CHAPTER 16 | OSCILLATORY MOTION AND WAVES
45. Suppose you have a 0.750-kg object on a horizontal surface
connected to a spring that has a force constant of 150 N/m. There is
simple friction between the object and surface with a static coefficient of
friction µ s = 0.100 . (a) How far can the spring be stretched without
moving the mass? (b) If the object is set into oscillation with an amplitude
twice the distance found in part (a), and the kinetic coefficient of friction is
µ k = 0.0850 , what total distance does it travel before stopping?
Assume it starts at the maximum amplitude.
46. Engineering Application: A suspension bridge oscillates with an
effective force constant of 1.00×108 N/m . (a) How much energy is
needed to make it oscillate with an amplitude of 0.100 m? (b) If soldiers
march across the bridge with a cadence equal to the bridge’s natural
frequency and impart 1.00×104 J of energy each second, how long
does it take for the bridge’s oscillations to go from 0.100 m to 0.500 m
amplitude?
16.9 Waves
Figure 16.48 A seismograph as described in above problem.(credit: Oleg Alexandrov)
47. Storms in the South Pacific can create waves that travel all the way to
the California coast, which are 12,000 km away. How long does it take
16.10 Superposition and Interference
them if they travel at 15.0 m/s?
57. A car has two horns, one emitting a frequency of 199 Hz and the
48. Waves on a swimming pool propagate at 0.750 m/s. You splash the
other emitting a frequency of 203 Hz. What beat frequency do they
water at one end of the pool and observe the wave go to the opposite
produce?
end, reflect, and return in 30.0 s. How far away is the other end of the
58. The middle-C hammer of a piano hits two strings, producing beats of
pool?
1.50 Hz. One of the strings is tuned to 260.00 Hz. What frequencies
49. Wind gusts create ripples on the ocean that have a wavelength of
could the other string have?
5.00 cm and propagate at 2.00 m/s. What is their frequency?
59. Two tuning forks having frequencies of 460 and 464 Hz are struck
50. How many times a minute does a boat bob up and down on ocean
simultaneously. What average frequency will you hear, and what will the
waves that have a wavelength of 40.0 m and a propagation speed of 5.00 beat frequency be?
m/s?
60. Twin jet engines on an airplane are producing an average sound
51. Scouts at a camp shake the rope bridge they have just crossed and
frequency of 4100 Hz with a beat frequency of 0.500 Hz. What are their
observe the wave crests to be 8.00 m apart. If they shake it the bridge
individual frequencies?
twice per second, what is the propagation speed of the waves?
61. A wave traveling on a Slinky® that is stretched to 4 m takes 2.4 s to
52. What is the wavelength of the waves you create in a swimming pool if
travel the length of the Slinky and back again. (a) What is the speed of
you splash your hand at a rate of 2.00 Hz and the waves propagate at
the wave? (b) Using the same Slinky stretched to the same length, a
0.800 m/s?
standing wave is created which consists of three antinodes and four
53. What is the wavelength of an earthquake that shakes you with a
nodes. At what frequency must the Slinky be oscillating?
frequency of 10.0 Hz and gets to another city 84.0 km away in 12.0 s?
62. Three adjacent keys on a piano (F, F-sharp, and G) are struck
simultaneously, producing frequencies of 349, 370, and 392 Hz. What
54. Radio waves transmitted through space at 3.00×108 m/s by the
beat frequencies are produced by this discordant combination?
Voyager spacecraft have a wavelength of 0.120 m. What is their
frequency?
16.11 Energy in Waves: Intensity
55. Your ear is capable of differentiating sounds that arrive at the ear just
63. Medical Application
1.00 ms apart. What is the minimum distance between two speakers that
produce sounds that arrive at noticeably different times on a day when
Ultrasound of intensity 1.50×102 W/m2 is produced by the rectangular
the speed of sound is 340 m/s?
head of a medical imaging device measuring 3.00 by 5.00 cm. What is its
56. (a) Seismographs measure the arrival times of earthquakes with a
power output?
precision of 0.100 s. To get the distance to the epicenter of the quake,
64. The low-frequency speaker of a stereo set has a surface area of
they compare the arrival times of S- and P-waves, which travel at
0.05 m2 and produces 1W of acoustical power. What is the intensity at
different speeds. Figure 16.48) If S- and P-waves travel at 4.00 and 7.20
km/s, respectively, in the region considered, how precisely can the
the speaker? If the speaker projects sound uniformly in all directions, at
distance to the source of the earthquake be determined? (b) Seismic
what distance from the speaker is the intensity 0.1 W/m2 ?
waves from underground detonations of nuclear bombs can be used to
locate the test site and detect violations of test bans. Discuss whether
65. To increase intensity of a wave by a factor of 50, by what factor
your answer to (a) implies a serious limit to such detection. (Note also
should the amplitude be increased?
that the uncertainty is greater if there is an uncertainty in the propagation
66. Engineering Application
speeds of the S- and P-waves.)
A device called an insolation meter is used to measure the intensity of
sunlight has an area of 100 cm2 and registers 6.50 W. What is the
intensity in W/m2 ?
67. Astronomy Application
Energy from the Sun arrives at the top of the Earth’s atmosphere with an
intensity of 1.30 kW/m2. How long does it take for 1.8×109 J to
arrive on an area of 1.00 m2 ?
CHAPTER 16 | OSCILLATORY MOTION AND WAVES 587
68. The low-frequency speaker of a stereo set has a surface area of
0.05 m2 and produces 1 W of acoustical power. What is the intensity at
the speaker? If the speaker projects sound uniformly in all directions, at
what distance from the speaker is the intensity 0.1 W/m2?
69. Suppose you have a device that extracts energy from ocean breakers
in direct proportion to their intensity. If the device produces 10.0 kW of
power on a day when the breakers are 1.20 m high, how much will it
produce when they are 0.600 m high?
70. Engineering Application
(a) A photovoltaic array of (solar cells) is 10.0% efficient in gathering
solar energy and converting it to electricity. If the average intensity of
sunlight on one day is 700 W/m2, what area should your array have to
gather energy at the rate of 100 W? (b) What is the maximum cost of the
array if it must pay for itself in two years of operation averaging 10.0
hours per day? Assume that it earns money at the rate of 9.00 ¢ per
kilowatt-hour.
71. A microphone receiving a pure sound tone feeds an oscilloscope,
producing a wave on its screen. If the sound intensity is originally
2.00×10–5 W/m2, but is turned up until the amplitude increases by
30.0%, what is the new intensity?
72. Medical Application
(a) What is the intensity in W/m2 of a laser beam used to burn away
cancerous tissue that, when 90.0% absorbed, puts 500 J of energy into a
circular spot 2.00 mm in diameter in 4.00 s? (b) Discuss how this
intensity compares to the average intensity of sunlight (about 1 W/m2 )
and the implications that would have if the laser beam entered your eye.
Note how your answer depends on the time duration of the exposure.
588 CHAPTER 16 | OSCILLATORY MOTION AND WAVES

CHAPTER 17 | PHYSICS OF HEARING 589
17
PHYSICS OF HEARING
Figure 17.1 This tree fell some time ago. When it fell, atoms in the air were disturbed. Physicists would call this disturbance sound whether someone was around to hear it or
not. (credit: B.A. Bowen Photography)
Learning Objectives
17.1. Sound
• Define sound and hearing.
• Describe sound as a longitudinal wave.
17.2. Speed of Sound, Frequency, and Wavelength
• Define pitch.
• Describe the relationship between the speed of sound, its frequency, and its wavelength.
• Describe the effects on the speed of sound as it travels through various media.
• Describe the effects of temperature on the speed of sound.
17.3. Sound Intensity and Sound Level
• Define intensity, sound intensity, and sound pressure level.
• Calculate sound intensity levels in decibels (dB).
17.4. Doppler Effect and Sonic Booms
• Define Doppler effect, Doppler shift, and sonic boom.
• Calculate the frequency of a sound heard by someone observing Doppler shift.
• Describe the sounds produced by objects moving faster than the speed of sound.
17.5. Sound Interference and Resonance: Standing Waves in Air Columns
• Define antinode, node, fundamental, overtones, and harmonics.
• Identify instances of sound interference in everyday situations.
• Describe how sound interference occurring inside open and closed tubes changes the characteristics of the sound, and how this applies
to sounds produced by musical instruments.
• Calculate the length of a tube using sound wave measurements.
17.6. Hearing
• Define hearing, pitch, loudness, timbre, note, tone, phon, ultrasound, and infrasound.
• Compare loudness to frequency and intensity of a sound.
• Identify structures of the inner ear and explain how they relate to sound perception.
17.7. Ultrasound
• Define acoustic impedance and intensity reflection coefficient.
• Describe medical and other uses of ultrasound technology.
• Calculate acoustic impedance using density values and the speed of ultrasound.
• Calculate the velocity of a moving object using Doppler-shifted ultrasound.

590 CHAPTER 17 | PHYSICS OF HEARING
Introduction to the Physics of Hearing
If a tree falls in the forest and no one is there to hear it, does it make a sound? The answer to this old philosophical question depends on how you
define sound. If sound only exists when someone is around to perceive it, then there was no sound. However, if we define sound in terms of physics;
that is, a disturbance of the atoms in matter transmitted from its origin outward (in other words, a wave), then there was a sound, even if nobody was
around to hear it.
Such a wave is the physical phenomenon we call sound. Its perception is hearing. Both the physical phenomenon and its perception are interesting
and will be considered in this text. We shall explore both sound and hearing; they are related, but are not the same thing. We will also explore the
many practical uses of sound waves, such as in medical imaging.
17.1 Sound
Figure 17.2 This glass has been shattered by a high-intensity sound wave of the same frequency as the resonant frequency of the glass. While the sound is not visible, the
effects of the sound prove its existence. (credit: ||read||, Flickr)
Sound can be used as a familiar illustration of waves. Because hearing is one of our most important senses, it is interesting to see how the physical
properties of sound correspond to our perceptions of it. Hearing is the perception of sound, just as vision is the perception of visible light. But sound
has important applications beyond hearing. Ultrasound, for example, is not heard but can be employed to form medical images and is also used in
treatment.
The physical phenomenon of sound is defined to be a disturbance of matter that is transmitted from its source outward. Sound is a wave. On the
atomic scale, it is a disturbance of atoms that is far more ordered than their thermal motions. In many instances, sound is a periodic wave, and the
atoms undergo simple harmonic motion. In this text, we shall explore such periodic sound waves.
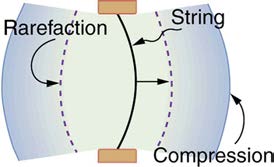
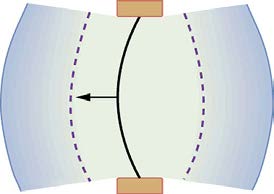
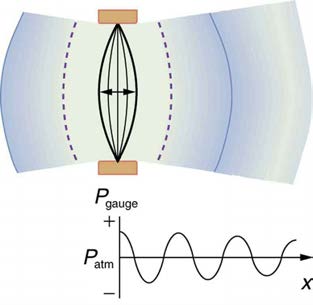
A vibrating string produces a sound wave as illustrated in Figure 17.3, Figure 17.4, and Figure 17.5. As the string oscillates back and forth, it
transfers energy to the air, mostly as thermal energy created by turbulence. But a small part of the string’s energy goes into compressing and
expanding the surrounding air, creating slightly higher and lower local pressures. These compressions (high pressure regions) and rarefactions (low
pressure regions) move out as longitudinal pressure waves having the same frequency as the string—they are the disturbance that is a sound wave.
(Sound waves in air and most fluids are longitudinal, because fluids have almost no shear strength. In solids, sound waves can be both transverse
and longitudinal.) Figure 17.5 shows a graph of gauge pressure versus distance from the vibrating string.
Figure 17.3 A vibrating string moving to the right compresses the air in front of it and expands the air behind it.
Figure 17.4 As the string moves to the left, it creates another compression and rarefaction as the ones on the right move away from the string.

CHAPTER 17 | PHYSICS OF HEARING 591
Figure 17.5 After many vibrations, there are a series of compressions and rarefactions moving out from the string as a sound wave. The graph shows gauge pressure versus
distance from the source. Pressures vary only slightly from atmospheric for ordinary sounds.
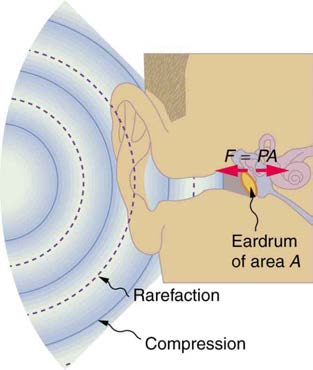
The amplitude of a sound wave decreases with distance from its source, because the energy of the wave is spread over a larger and larger area. But
it is also absorbed by objects, such as the eardrum in Figure 17.6, and converted to thermal energy by the viscosity of air. In addition, during each compression a little heat transfers to the ai












