produces a combination of constructive and destructive interference and can vary from place to place and time to time. Sound from a stereo, for
example, can be loud in one spot and quiet in another. Varying loudness means the sound waves add partially constructively and partially
destructively at different locations. A stereo has at least two speakers creating sound waves, and waves can reflect from walls. All these waves
superimpose. An example of sounds that vary over time from constructive to destructive is found in the combined whine of airplane jets heard by a
stationary passenger. The combined sound can fluctuate up and down in volume as the sound from the two engines varies in time from constructive
to destructive. These examples are of waves that are similar.
An example of the superposition of two dissimilar waves is shown in Figure 16.38. Here again, the disturbances add and subtract, producing a more
complicated looking wave.
Figure 16.38 Superposition of non-identical waves exhibits both constructive and destructive interference.
Standing Waves
Sometimes waves do not seem to move; rather, they just vibrate in place. Unmoving waves can be seen on the surface of a glass of milk in a
refrigerator, for example. Vibrations from the refrigerator motor create waves on the milk that oscillate up and down but do not seem to move across
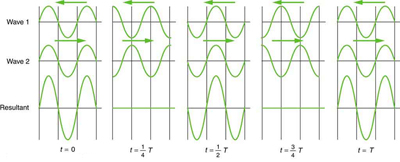
the surface. These waves are formed by the superposition of two or more moving waves, such as illustrated in Figure 16.39 for two identical waves
moving in opposite directions. The waves move through each other with their disturbances adding as they go by. If the two waves have the same
amplitude and wavelength, then they alternate between constructive and destructive interference. The resultant looks like a wave standing in place
and, thus, is called a standing wave. Waves on the glass of milk are one example of standing waves. There are other standing waves, such as on
guitar strings and in organ pipes. With the glass of milk, the two waves that produce standing waves may come from reflections from the side of the
glass.
A closer look at earthquakes provides evidence for conditions appropriate for resonance, standing waves, and constructive and destructive
interference. A building may be vibrated for several seconds with a driving frequency matching that of the natural frequency of vibration of the
building—producing a resonance resulting in one building collapsing while neighboring buildings do not. Often buildings of a certain height are
devastated while other taller buildings remain intact. The building height matches the condition for setting up a standing wave for that particular
height. As the earthquake waves travel along the surface of Earth and reflect off denser rocks, constructive interference occurs at certain points.
Often areas closer to the epicenter are not damaged while areas farther away are damaged.
576 CHAPTER 16 | OSCILLATORY MOTION AND WAVES
Figure 16.39 Standing wave created by the superposition of two identical waves moving in opposite directions. The oscillations are at fixed locations in space and result from
alternately constructive and destructive interference.
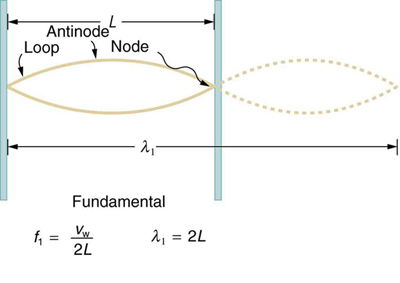
Standing waves are also found on the strings of musical instruments and are due to reflections of waves from the ends of the string. Figure 16.40
and Figure 16.41 show three standing waves that can be created on a string that is fixed at both ends. Nodes are the points where the string does not move; more generally, nodes are where the wave disturbance is zero in a standing wave. The fixed ends of strings must be nodes, too, because
the string cannot move there. The word antinode is used to denote the location of maximum amplitude in standing waves. Standing waves on strings
have a frequency that is related to the propagation speed v w of the disturbance on the string. The wavelength λ is determined by the distance
between the points where the string is fixed in place.
The lowest frequency, called the fundamental frequency, is thus for the longest wavelength, which is seen to be λ 1 = 2 L . Therefore, the
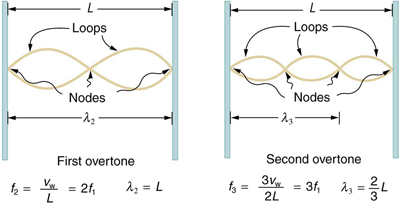
fundamental frequency is f 1 = v w / λ 1 = v w / 2 L . In this case, the overtones or harmonics are multiples of the fundamental frequency. As seen in
Figure 16.41, the first harmonic can easily be calculated since λ 2 = L . Thus, f 2 = v w / λ 2 = v w / 2 L = 2 f 1 . Similarly, f 3 = 3 f 1 , and so on. All of these frequencies can be changed by adjusting the tension in the string. The greater the tension, the greater v w is and the higher the frequencies.
This observation is familiar to anyone who has ever observed a string instrument being tuned. We will see in later chapters that standing waves are
crucial to many resonance phenomena, such as in sounding boxes on string instruments.
Figure 16.40 The figure shows a string oscillating at its fundamental frequency.
Figure 16.41 First and second harmonic frequencies are shown.
CHAPTER 16 | OSCILLATORY MOTION AND WAVES 577
Beats
Striking two adjacent keys on a piano produces a warbling combination usually considered to be unpleasant. The superposition of two waves of
similar but not identical frequencies is the culprit. Another example is often noticeable in jet aircraft, particularly the two-engine variety, while taxiing.
The combined sound of the engines goes up and down in loudness. This varying loudness happens because the sound waves have similar but not
identical frequencies. The discordant warbling of the piano and the fluctuating loudness of the jet engine noise are both due to alternately
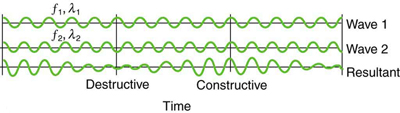
constructive and destructive interference as the two waves go in and out of phase. Figure 16.42 illustrates this graphically.
Figure 16.42 Beats are produced by the superposition of two waves of slightly different frequencies but identical amplitudes. The waves alternate in time between constructive
interference and destructive interference, giving the resulting wave a time-varying amplitude.
The wave resulting from the superposition of two similar-frequency waves has a frequency that is the average of the two. This wave fluctuates in
amplitude, or beats, with a frequency called the beat frequency. We can determine the beat frequency by adding two waves together
mathematically. Note that a wave can be represented at one point in space as
⎞
(16.69)
x = X cos⎛2π t
⎝ T ⎠ = X cos⎛⎝2π ft⎞⎠,
where f = 1 / T is the frequency of the wave. Adding two waves that have different frequencies but identical amplitudes produces a resultant
x = x
(16.70)
1 + x 2.
More specifically,
(16.71)
x = X cos⎛⎝2π f 1 t⎞⎠ + X cos⎛⎝2π f 2 t⎞⎠.
Using a trigonometric identity, it can be shown that
(16.72)
x = 2 X cos⎛⎝ π f B t⎞⎠cos⎛⎝2π f ave t⎞⎠,
where
f
(16.73)
B = ∣ f 1 − f 2 ∣
is the beat frequency, and f ave is the average of f 1 and f 2 . These results mean that the resultant wave has twice the amplitude and the average
frequency of the two superimposed waves, but it also fluctuates in overall amplitude at the beat frequency f B . The first cosine term in the
expression effectively causes the amplitude to go up and down. The second cosine term is the wave with frequency f ave . This result is valid for all
types of waves. However, if it is a sound wave, providing the two frequencies are similar, then what we hear is an average frequency that gets louder
and softer (or warbles) at the beat frequency.
Making Career Connections
Piano tuners use beats routinely in their work. When comparing a note with a tuning fork, they listen for beats and adjust the string until the beats
go away (to zero frequency). For example, if the tuning fork has a 256 Hz frequency and two beats per second are heard, then the other
frequency is either 254 or 258 Hz . Most keys hit multiple strings, and these strings are actually adjusted until they have nearly the same
frequency and give a slow beat for richness. Twelve-string guitars and mandolins are also tuned using beats.
While beats may sometimes be annoying in audible sounds, we will find that beats have many applications. Observing beats is a very useful way to
compare similar frequencies. There are applications of beats as apparently disparate as in ultrasonic imaging and radar speed traps.
Check Your Understanding
Imagine you are holding one end of a jump rope, and your friend holds the other. If your friend holds her end still, you can move your end up and
down, creating a transverse wave. If your friend then begins to move her end up and down, generating a wave in the opposite direction, what
resultant wave forms would you expect to see in the jump rope?
Solution
The rope would alternate between having waves with amplitudes two times the original amplitude and reaching equilibrium with no amplitude at
all. The wavelengths will result in both constructive and destructive interference
Check Your Understanding
Define nodes and antinodes.
Solution


578 CHAPTER 16 | OSCILLATORY MOTION AND WAVES
Nodes are areas of wave interference where there is no motion. Antinodes are areas of wave interference where the motion is at its maximum
point.
Check Your Understanding
You hook up a stereo system. When you test the system, you notice that in one corner of the room, the sounds seem dull. In another area, the
sounds seem excessively loud. Describe how the sound moving about the room could result in these effects.
Solution
With multiple speakers putting out sounds into the room, and these sounds bouncing off walls, there is bound to be some wave interference. In
the dull areas, the interference is probably mostly destructive. In the louder areas, the interference is probably mostly constructive.
PhET Explorations: Wave Interference
Make waves with a dripping faucet, audio speaker, or laser! Add a second source or a pair of slits to create an interference pattern.
Figure 16.43 Wave Interference (http://cnx.org/content/m42249/1.4/wave-interference_en.jar)
16.11 Energy in Waves: Intensity
Figure 16.44 The destructive effect of an earthquake is palpable evidence of the energy carried in these waves. The Richter scale rating of earthquakes is related to both their amplitude and the energy they carry. (credit: Petty Officer 2nd Class Candice Villarreal, U.S. Navy)
All waves carry energy. The energy of some waves can be directly observed. Earthquakes can shake whole cities to the ground, performing the work
of thousands of wrecking balls.
Loud sounds pulverize nerve cells in the inner ear, causing permanent hearing loss. Ultrasound is used for deep-heat treatment of muscle strains. A
laser beam can burn away a malignancy. Water waves chew up beaches.
The amount of energy in a wave is related to its amplitude. Large-amplitude earthquakes produce large ground displacements. Loud sounds have
higher pressure amplitudes and come from larger-amplitude source vibrations than soft sounds. Large ocean breakers churn up the shore more than
small ones. More quantitatively, a wave is a displacement that is resisted by a restoring force. The larger the displacement x , the larger the force
F = kx needed to create it. Because work W is related to force multiplied by distance ( Fx ) and energy is put into the wave by the work done to
create it, the energy in a wave is related to amplitude. In fact, a wave’s energy is directly proportional to its amplitude squared because
(16.74)
W ∝ Fx = kx 2.
The energy effects of a wave depend on time as well as amplitude. For example, the longer deep-heat ultrasound is applied, the more energy it
transfers. Waves can also be concentrated or spread out. Sunlight, for example, can be focused to burn wood. Earthquakes spread out, so they do
less damage the farther they get from the source. In both cases, changing the area the waves cover has important effects. All these pertinent factors
are included in the definition of intensity I as power per unit area:
(16.75)
I = PA
where P is the power carried by the wave through area A . The definition of intensity is valid for any energy in transit, including that carried by
waves. The SI unit for intensity is watts per square meter ( W/m2 ). For example, infrared and visible energy from the Sun impinge on Earth at an
intensity of 1300 W/m2 just above the atmosphere. There are other intensity-related units in use, too. The most common is the decibel. For
example, a 90 decibel sound level corresponds to an intensity of 10−3 W/m2 . (This quantity is not much power per unit area considering that 90
decibels is a relatively high sound level. Decibels will be discussed in some detail in a later chapter.
CHAPTER 16 | OSCILLATORY MOTION AND WAVES 579
Example 16.9 Calculating intensity and power: How much energy is in a ray of sunlight?
The average intensity of sunlight on Earth’s surface is about 700 W/m2 .
(a) Calculate the amount of energy that falls on a solar collector having an area of 0.500 m2 in 4.00 h .
(b) What intensity would such sunlight have if concentrated by a magnifying glass onto an area 200 times smaller than its own?
Strategy a
Because power is energy per unit time or P = Et , the definition of intensity can be written as I = PA = E / t
A , and this equation can be solved
for E with the given information.
Solution a
1. Begin with the equation that states the definition of intensity:
(16.76)
I = PA.
2. Replace P with its equivalent E / t :
(16.77)
I = E / t
A .
3. Solve for E :
E
(16.78)
= IAt.
4. Substitute known values into the equation:
⎛
⎡
(16.79)
E = ⎛⎝700 W/m2⎞⎠⎝0.500 m2⎞⎠⎣(4.00 h)(3600 s/h)⎤⎦.
5. Calculate to find E and convert units:
(16.80)
5.04×106 J,
Discussion a
The energy falling on the solar collector in 4 h in part is enough to be useful—for example, for heating a significant amount of water.
Strategy b
Taking a ratio of new intensity to old intensity and using primes for the new quantities, we will find that it depends on the ratio of the areas. All
other quantities will cancel.
Solution b
1. Take the ratio of intensities, which yields:
⎛
(16.81)
I′ I = P′/ A′
P / A = A
A′ ⎝The powers cancel because P′ = P⎞⎠.
2. Identify the knowns:
A
(16.82)
= 200 A′,
I
(16.83)
′ I = 200.
3. Substitute known quantities:
(16.84)
I′ = 200 I = 200⎛⎝700 W/m2⎞⎠.
4. Calculate to find I′ :
(16.85)
I′ = 1.40×105 W/m2.
Discussion b
Decreasing the area increases the intensity considerably. The intensity of the concentrated sunlight could even start a fire.
Example 16.10 Determine the combined intensity of two waves: Perfect constructive interference
If two identical waves, each having an intensity of 1.00 W/m2 , interfere perfectly constructively, what is the intensity of the resulting wave?
Strategy
We know from Superposition and Interference that when two identical waves, which have equal amplitudes X , interfere perfectly
constructively, the resulting wave has an amplitude of 2 X . Because a wave’s intensity is proportional to amplitude squared, the intensity of the
resulting wave is four times as great as in the individual waves.
Solution
1. Recall that intensity is proportional to amplitude squared.
2. Calculate the new amplitude:
(16.86)
I′ ∝ ( X′)2 = (2 X)2 = 4 X 2.
3. Recall that the intensity of the old amplitude was:
580 CHAPTER 16 | OSCILLATORY MOTION AND WAVES
(16.87)
I ∝ X 2.
4. Take the ratio of new intensity to the old intensity. This gives: I
(16.88)
′ I = 4.
5. Calculate to find I′ :
(16.89)
I′ = 4 I = 4.00 W/m2.
Discussion
The intensity goes up by a factor of 4 when the amplitude doubles. This answer is a little disquieting. The two individual waves each have
intensities of 1.00 W/m2 , yet their sum has an intensity of 4.00 W/m2 , which may appear to violate conservation of energy. This violation, of
course, cannot happen. What does happen is intriguing. The area over which the intensity is 4.00 W/m2 is much less than the area covered by
the two waves before they interfered. There are other areas where the intensity is zero. The addition of waves is not as simple as our first look in
Superposition and Interference suggested. We actually get a pattern of both constructive interference and destructive interference whenever
two waves are added. For example, if we have two stereo speakers putting out 1.00 W/m2 each, there will be places in the room where the
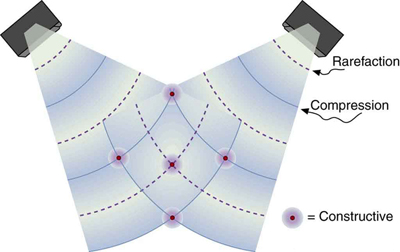
intensity is 4.00 W/m2 , other places where the intensity is zero, and others in between. Figure 16.45 shows what this interference might look
like. We will pursue interference patterns elsewhere in this text.
Figure 16.45 These stereo speakers produce both constructive interference and destructive interference in the room, a property common to the superposition of all types
of waves. The shading is proportional to intensity.
Check Your Understanding
Which measurement of a wave is most important when determining the wave's intensity?
Solution
Amplitude, because a wave’s energy is directly proportional to its amplitude squared.
Glossary
amplitude: the maximum displacement from the equilibrium position of an object oscillating around the equilibrium position
antinode: the location of maximum amplitude in standing waves
beat frequency: the frequency of the amplitude fluctuations of a wave
constructive interference: when two waves arrive at the same point exactly in phase; that is, the crests of the two waves are precisely aligned,
as are the troughs
critical damping: the condition in which the damping of an oscillator causes it to return as quickly as possible to its equilibrium position without
oscillating back and forth about this position
deformation: displacement from equilibrium
destructive interference: when two identical waves arrive at the same point exactly out of phase; that is, precisely aligned crest to trough
elastic potential energy: potential energy stored as a result of deformation of an elastic object, such as the stretching of a spring
force constant: a constant related to the rigidity of a system: the larger the force constant, the more rigid the system; the force constant is
represented by k
frequency: number of events per unit of time
fundamental frequency: the lowest frequency of a periodic waveform
intensity: power per unit area
CHAPTER 16 | OSCILLATORY MOTION AND WAVES 581
longitudinal wave: a wave in which the disturbance is parallel to the direction of propagation
natural frequency: the frequency at which a system would oscillate if there were no driving and no damping forces
nodes: the points where the string does not move; more generally, nodes are where the wave disturbance is zero in a standing wave
oscillate: moving back and forth regularly between two points
over damping: the condition in which damping of an oscillator causes it to return to equilibrium without oscillating; oscillator moves more slowly
toward equilibrium than in the critically damped system
overtones: multiples of the fundamental frequency of a sound
periodic motion: motion that repeats itself at regular time intervals
period: time it takes to complete one oscillation
resonance: the phenomenon of driving a system with a frequency equal to the system's natural frequency
resonate: a system being driven at its natural frequency
restoring force: force acting in opposition to the force caused by a deformation
simple harmonic motion: the oscillatory motion in a system where the net force can be described by Hooke’s law
simple harmonic oscillator: a device that implements Hooke’s law, such as a mass that is attached to a spring, with the other end of the spring
being connected to a rigid support such as a wall
simple pendulum: an object with a small mass suspended from a light wire or string
superposition: the phenomenon that occurs when two or more waves arrive at the same point
transverse wave: a wave in which the disturbance is perpendicular to the direction of propagation
under damping: the condition in which damping of an oscillator causes it to return to equilibrium with the amplitude gradually decreasing to zero;
system returns to equilibrium faster but overshoots and crosses the equilibrium position one or more times
wave velocity: the speed at which the disturbance moves. Also called the propagation velocity or propagation speed
wavelength: the distance between adjacent identical parts of a wave<










