(16.44)
v max = 6.53×104 N/m
900 kg
(0.100 m).
3. Calculate to find v max= 0.852 m/s.
Discussion
This answer seems reasonable for a bouncing car. There are other ways to use conservation of energy to find v max . We could use it directly, as
was done in the example featured in Hooke’s Law: Stress and Strain Revisited.
The small vertical displacement y of an oscillating simple pendulum, starting from its equilibrium position, is given as
y
(16.45)
( t) = a sin ωt,
where a is the amplitude, ω is the angular velocity and t is the time taken. Substituting ω = 2π
T , we have
⎞
(16.46)
yt = a sin⎛2π t
⎝ T ⎠.
Thus, the displacement of pendulum is a function of time as shown above.
Also the velocity of the pendulum is given by
⎞
(16.47)
v( t) = 2 aπ
2π t
T cos ⎛⎝ T ⎠,
so the motion of the pendulum is a function of time.
Check Your Understanding
Why does it hurt more if your hand is snapped with a ruler than with a loose spring, even if the displacement of each system is equal?
Solution

564 CHAPTER 16 | OSCILLATORY MOTION AND WAVES
The ruler is a stiffer system, which carries greater force for the same amount of displacement. The ruler snaps your hand with greater force,
which hurts more.
Check Your Understanding
You are observing a simple harmonic oscillator. Identify one way you could decrease the maximum velocity of the system.
Solution
You could increase the mass of the object that is oscillating.
16.6 Uniform Circular Motion and Simple Harmonic Motion
Figure 16.17 The horses on this merry-go-round exhibit uniform circular motion. (credit: Wonderlane, Flickr)
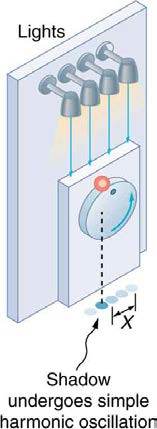
There is an easy way to produce simple harmonic motion by using uniform circular motion. Figure 16.18 shows one way of using this method. A ball
is attached to a uniformly rotating vertical turntable, and its shadow is projected on the floor as shown. The shadow undergoes simple harmonic
motion. Hooke’s law usually describes uniform circular motions ( ω constant) rather than systems that have large visible displacements. So
observing the projection of uniform circular motion, as in Figure 16.18, is often easier than observing a precise large-scale simple harmonic oscillator.
If studied in sufficient depth, simple harmonic motion produced in this manner can give considerable insight into many aspects of oscillations and
waves and is very useful mathematically. In our brief treatment, we shall indicate some of the major features of this relationship and how they might
be useful.
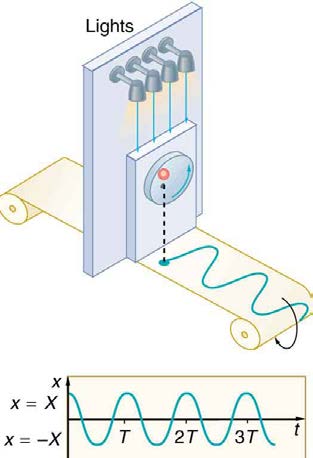
Figure 16.18 The shadow of a ball rotating at constant angular velocity ω on a turntable goes back and forth in precise simple harmonic motion.
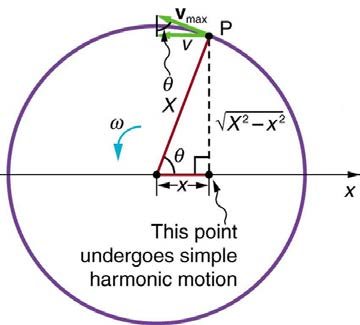
Figure 16.19 shows the basic relationship between uniform circular motion and simple harmonic motion. The point P travels around the circle at
constant angular velocity ω . The point P is analogous to an object on the merry-go-round. The projection of the position of P onto a fixed axis
undergoes simple harmonic motion and is analogous to the shadow of the object. At the time shown in the figure, the projection has position x and
moves to the left with velocity v . The velocity of the point P around the circle equals v¯ max .The projection of v¯ max on the x -axis is the velocity v of the simple harmonic motion along the x -axis.
CHAPTER 16 | OSCILLATORY MOTION AND WAVES 565
Figure 16.19 A point P moving on a circular path with a constant angular velocity ω is undergoing uniform circular motion. Its projection on the x-axis undergoes simple harmonic motion. Also shown is the velocity of this point around the circle, v¯ max , and its projection, which is v . Note that these velocities form a similar triangle to the displacement triangle.
To see that the projection undergoes simple harmonic motion, note that its position x is given by
x
(16.48)
= X cos θ,
where θ = ωt , ω is the constant angular velocity, and X is the radius of the circular path. Thus,
x
(16.49)
= X cos ωt.
The angular velocity ω is in radians per unit time; in this case 2π radians is the time for one revolution T . That is, ω = 2π / T . Substituting this expression for ω , we see that the position x is given by:
⎞
(16.50)
x( t) = cos⎛2π t
⎝ T ⎠.
This expression is the same one we had for the position of a simple harmonic oscillator in Simple Harmonic Motion: A Special Periodic Motion. If
we make a graph of position versus time as in Figure 16.20, we see again the wavelike character (typical of simple harmonic motion) of the
projection of uniform circular motion onto the x -axis.
Figure 16.20 The position of the projection of uniform circular motion performs simple harmonic motion, as this wavelike graph of x versus t indicates.
Now let us use Figure 16.19 to do some further analysis of uniform circular motion as it relates to simple harmonic motion. The triangle formed by the velocities in the figure and the triangle formed by the displacements ( X, x, and X 2 − x 2 ) are similar right triangles. Taking ratios of similar sides,
we see that
(16.51)
v
v
= X 2 − x 2
max
X
= 1 − x 2
X 2.
We can solve this equation for the speed v or

566 CHAPTER 16 | OSCILLATORY MOTION AND WAVES
(16.52)
v = v max 1 − x 2
X 2.
This expression for the speed of a simple harmonic oscillator is exactly the same as the equation obtained from conservation of energy
considerations in Energy and the Simple Harmonic Oscillator.You can begin to see that it is possible to get all of the characteristics of simple
harmonic motion from an analysis of the projection of uniform circular motion.
Finally, let us consider the period T of the motion of the projection. This period is the time it takes the point P to complete one revolution. That time
is the circumference of the circle 2π X divided by the velocity around the circle, v max . Thus, the period T is
(16.53)
T = 2πX
v
.
max
We know from conservation of energy considerations that
(16.54)
v max = kmX.
Solving this equation for X / v max gives
X
(16.55)
v
= m
max
k .
Substituting this expression into the equation for T yields
(16.56)
T = 2π mk.
Thus, the period of the motion is the same as for a simple harmonic oscillator. We have determined the period for any simple harmonic oscillator
using the relationship between uniform circular motion and simple harmonic motion.
Some modules occasionally refer to the connection between uniform circular motion and simple harmonic motion. Moreover, if you carry your study of
physics and its applications to greater depths, you will find this relationship useful. It can, for example, help to analyze how waves add when they are
superimposed.
Check Your Understanding
Identify an object that undergoes uniform circular motion. Describe how you could trace the simple harmonic motion of this object as a wave.
Solution
A record player undergoes uniform circular motion. You could attach dowel rod to one point on the outside edge of the turntable and attach a pen
to the other end of the dowel. As the record player turns, the pen will move. You can drag a long piece of paper under the pen, capturing its
motion as a wave.
16.7 Damped Harmonic Motion
Figure 16.21 In order to counteract dampening forces, this dad needs to keep pushing the swing. (credit: Erik A. Johnson, Flickr)
A guitar string stops oscillating a few seconds after being plucked. To keep a child happy on a swing, you must keep pushing. Although we can often
make friction and other non-conservative forces negligibly small, completely undamped motion is rare. In fact, we may even want to damp
oscillations, such as with car shock absorbers.
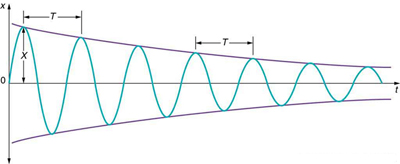
For a system that has a small amount of damping, the period and frequency are nearly the same as for simple harmonic motion, but the amplitude
gradually decreases as shown in Figure 16.22. This occurs because the non-conservative damping force removes energy from the system, usually in
the form of thermal energy. In general, energy removal by non-conservative forces is described as
W
(16.57)
nc = Δ(KE + PE),
where W nc is work done by a non-conservative force (here the damping force). For a damped harmonic oscillator, W nc is negative because it
removes mechanical energy (KE + PE) from the system.
CHAPTER 16 | OSCILLATORY MOTION AND WAVES 567
Figure 16.22 In this graph of displacement versus time for a harmonic oscillator with a small amount of damping, the amplitude slowly decreases, but the period and frequency
are nearly the same as if the system were completely undamped.
If you gradually increase the amount of damping in a system, the period and frequency begin to be affected, because damping opposes and hence
slows the back and forth motion. (The net force is smaller in both directions.) If there is very large damping, the system does not even oscillate—it
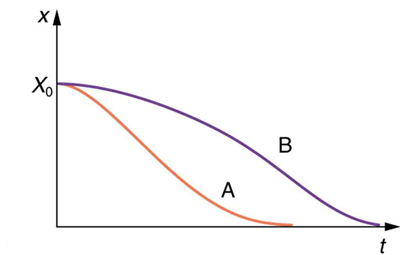
slowly moves toward equilibrium. Figure 16.23 shows the displacement of a harmonic oscillator for different amounts of damping. When we want to
damp out oscillations, such as in the suspension of a car, we may want the system to return to equilibrium as quickly as possible Critical damping is
defined as the condition in which the damping of an oscillator results in it returning as quickly as possible to its equilibrium position The critically
damped system may overshoot the equilibrium position, but if it does, it will do so only once. Critical damping is represented by Curve A in Figure
16.23. With less-than critical damping, the system will return to equilibrium faster but will overshoot and cross over one or more times. Such a system is underdamped; its displacement is represented by the curve in Figure 16.22. Curve B in Figure 16.23 represents an overdamped system. As with critical damping, it too may overshoot the equilibrium position, but will reach equilibrium over a longer period of time.
Figure 16.23 Displacement versus time for a critically damped harmonic oscillator (A) and an overdamped harmonic oscillator (B). The critically damped oscillator returns to
equilibrium at X = 0 in the smallest time possible without overshooting.
Critical damping is often desired, because such a system returns to equilibrium rapidly and remains at equilibrium as well. In addition, a constant
force applied to a critically damped system moves the system to a new equilibrium position in the shortest time possible without overshooting or
oscillating about the new position. For example, when you stand on bathroom scales that have a needle gauge, the needle moves to its equilibrium
position without oscillating. It would be quite inconvenient if the needle oscillated about the new equilibrium position for a long time before settling.
Damping forces can vary greatly in character. Friction, for example, is sometimes independent of velocity (as assumed in most places in this text).
But many damping forces depend on velocity—sometimes in complex ways, sometimes simply being proportional to velocity.
Example 16.7 Damping an Oscillatory Motion: Friction on an Object Connected to a Spring
Damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. This is generally attained using
non-conservative forces such as the friction between surfaces, and viscosity for objects moving through fluids. The following example considers
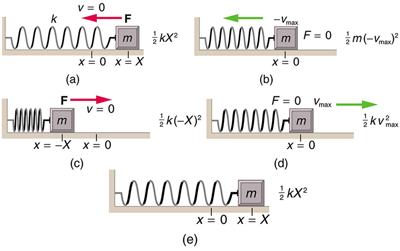
friction. Suppose a 0.200-kg object is connected to a spring as shown in Figure 16.24, but there is simple friction between the object and the
surface, and the coefficient of friction µk is equal to 0.0800. (a) What is the frictional force between the surfaces? (b) What total distance does
the object travel if it is released 0.100 m from equilibrium, starting at v = 0 ? The force constant of the spring is k = 50.0 N/m .
568 CHAPTER 16 | OSCILLATORY MOTION AND WAVES
Figure 16.24 The transformation of energy in simple harmonic motion is illustrated for an object attached to a spring on a frictionless surface.
Strategy
This problem requires you to integrate your knowledge of various concepts regarding waves, oscillations, and damping. To solve an integrated
concept problem, you must first identify the physical principles involved. Part (a) is about the frictional force. This is a topic involving the
application of Newton’s Laws. Part (b) requires an understanding of work and conservation of energy, as well as some understanding of
horizontal oscillatory systems.
Now that we have identified the principles we must apply in order to solve the problems, we need to identify the knowns and unknowns for each
part of the question, as well as the quantity that is constant in Part (a) and Part (b) of the question.
Solution a
1. Choose the proper equation: Friction is f = µ k mg .
2. Identify the known values.
3. Enter the known values into the equation:
(16.58)
f = (0.0800)(0.200 kg)(9.80 m / s2 ).
4. Calculate and convert units: f = 0.157 N.
Discussion a
The force here is small because the system and the coefficients are small.
Solution b
Identify the known:
• The system involves elastic potential energy as the spring compresses and expands, friction that is related to the work done, and the
kinetic energy as the body speeds up and slows down.
• Energy is not conserved as the mass oscillates because friction is a non-conservative force.
• The motion is horizontal, so gravitational potential energy does not need to be considered.
• Because the motion starts from rest, the energy in the system is initially PEel,i = (1 / 2) kX 2 . This energy is removed by work done by
friction W nc = – fd , where d is the total distance traveled and f = µ k mg is the force of friction. When the system stops moving, the friction force will balance the force exerted by the spring, so PEe1,f = (1 / 2) kx 2 where x is the final position and is given by
F
(16.59)
el = f
kx = µ k mg.
x
= µ k mg
k
1. By equating the work done to the energy removed, solve for the distance d .
2. The work done by the non-conservative forces equals the initial, stored elastic potential energy. Identify the correct equation to use:
⎛
2
(16.60)
W
µ
⎞
nc = Δ(KE + PE) = PE
k mg
el,f − PEel,i = 12 k⎜⎛
− X 2⎞⎟.
⎝⎝ k ⎠
⎠
3. Recall that W nc = – fd .
4. Enter the friction as f = µ k mg into W nc = – fd , thus W
(16.61)
nc = – µ k mgd.
5. Combine these two equations to find

CHAPTER 16 | OSCILLATORY MOTION AND WAVES 569
⎛
2
(16.62)
1 µk mg⎞
2 k⎜⎛
− X 2⎞⎟ = − µ
⎝⎝ k ⎠
⎠
k mgd.
6. Solve the equation for d :
⎛
2⎞
(16.63)
d =
k
µ k mg⎞
2 µ
⎜ X 2 – ⎛
⎟.
k mg⎝
⎝ k ⎠ ⎠
7. Enter the known values into the resulting equation:
⎛
2⎞
(16.64)
⎛(0.0800)⎛
⎛
⎞
d =
50.0 N/m
⎜(0.100 m)2 − ⎜
⎝0.200 kg⎞⎠⎝9.80 m/s2⎞⎠⎟ ⎟.
2(0.0800)⎛
⎛
⎜
50.0 N/m
⎟
⎝0.200 kg⎞⎠⎝9.80 m/s2⎞⎠⎝
⎝
⎠ ⎠
8. Calculate d and convert units:
d
(16.65)
= 1.59 m.
Discussion b
This is the total distance traveled back and forth across x = 0 , which is the undamped equilibrium position. The number of oscillations about
the equilibrium position will be more than d / X = (1.59 m) / (0.100 m) = 15.9 because the amplitude of the oscillations is decreasing with
time. At the end of the motion, this system will not return to x = 0 for this type of damping force, because static friction will exceed the restoring
force. This system is underdamped. In contrast, an overdamped system with a simple constant damping force would not cross the equilibrium
position x = 0 a single time. For example, if this system had a damping force 20 times greater, it would only move 0.0484 m toward the
equilibrium position from its original 0.100-m position.
This worked example illustrates how to apply problem-solving strategies to situations that integrate the different concepts you have learned. The
first step is to identify the physical principles involved in the problem. The second step is to solve for the unknowns using familiar problem-solving
strategies. These are found throughout the text, and many worked examples show how to use them for single topics. In this integrated concepts
example, you can see how to apply them across several topics. You will find these techniques useful in applications of physics outside a physics
course, such as in your profession, in other science disciplines, and in everyday life.
Check Your Understanding
Why are completely undamped harmonic oscillators so rare?
Solution
Friction often comes into play whenever an object is moving. Friction causes damping in a harmonic oscillator.
Check Your Understanding
Describe the difference between overdamping, underdamping, and critical damping.
Solution
An overdamped system moves slowly toward equilibrium. An underdamped system moves quickly to equilibrium, but will oscillate about the
equilibrium point as it does so. A critically damped system moves as quickly as possible toward equilibrium without oscillating about the
equilibrium.
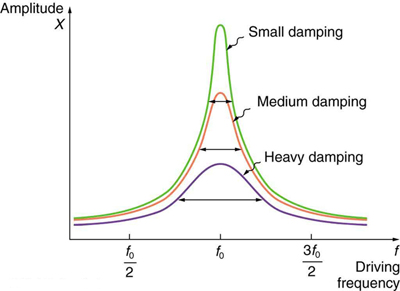
16.8 Forced Oscillations and Resonance
Figure 16.25 You can cause the strings in a piano to vibrate simply by producing sound waves from your voice. (credit: Matt Billings, Flickr)
Sit in front of a piano sometime and sing a loud brief note at it with the dampers off its strings. It will sing the same note back at you—the strings,
having the same frequencies as your voice, are resonating in response to the forces from the sound waves that you sent to them. Your voice and a
piano’s strings is a good example of the fact that objects—in this case, piano strings—can be forced to oscillate but oscillate best at their natural
frequency. In this section, we shall briefly explore applying a periodic driving force acting on a simple harmonic oscillator. The driving force puts
energy into the system at a certain frequency, not necessarily the same as the natural frequency of the system. The natural frequency is the
frequency at which a system would oscillate if there were no driving and no damping force.
570 CHAPTER 16 | OSCILLATORY MOTION AND WAVES
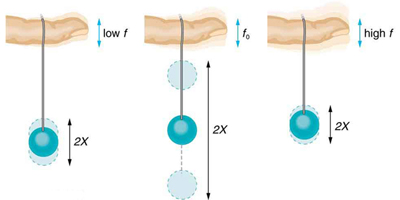
Most of us have played with toys involving an object supported on an elastic band, something like the paddle ball suspended from a finger in Figure
16.26. Imagine the finger in the figure is your finger. At first you hold your finger steady, and the ball bounces up and down with a small amount of damping. If you move your finger up and down slowly, the ball will follow along without bouncing much on its own. As you increase the frequency at














