or for work to be done.
Entropy increases in a closed system, such as the universe. But in parts of the universe, for instance, in the Solar system, it is not a locally closed
system. Energy flows from the Sun to the planets, replenishing Earth’s stores of energy. The Sun will continue to supply us with energy for about
another five billion years. We will enjoy direct solar energy, as well as side effects of solar energy, such as wind power and biomass energy from
photosynthetic plants. The energy from the Sun will keep our water at the liquid state, and the Moon’s gravitational pull will continue to provide tidal
energy. But Earth’s geothermal energy will slowly run down and won’t be replenished.
But in terms of the universe, and the very long-term, very large-scale picture, the entropy of the universe is increasing, and so the availability of
energy to do work is constantly decreasing. Eventually, when all stars have died, all forms of potential energy have been utilized, and all
temperatures have equalized (depending on the mass of the universe, either at a very high temperature following a universal contraction, or a very
low one, just before all activity ceases) there will be no possibility of doing work.
Either way, the universe is destined for thermodynamic equilibrium—maximum entropy. This is often called the heat death of the universe, and will
mean the end of all activity. However, whether the universe contracts and heats up, or continues to expand and cools down, the end is not near.
Calculations of black holes suggest that entropy can easily continue for at least 10100 years.
Order to Disorder
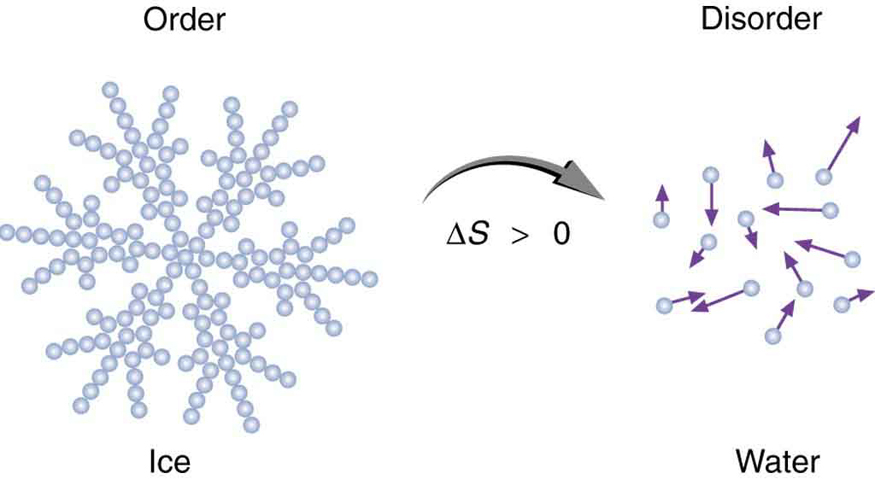
Entropy is related not only to the unavailability of energy to do work—it is also a measure of disorder. This notion was initially postulated by Ludwig
Boltzmann in the 1800s. For example, melting a block of ice means taking a highly structured and orderly system of water molecules and converting it
into a disorderly liquid in which molecules have no fixed positions. (See Figure 15.36.) There is a large increase in entropy in the process, as seen in
the following example.
Example 15.8 Entropy Associated with Disorder
Find the increase in entropy of 1.00 kg of ice originally at 0º C that is melted to form water at 0º C .
Strategy
As before, the change in entropy can be calculated from the definition of Δ S once we find the energy Q needed to melt the ice.
Solution
The change in entropy is defined as:
(15.61)
ΔS = QT.
Here Q is the heat transfer necessary to melt 1.00 kg of ice and is given by
Q
(15.62)
= mL f,
where m is the mass and L f is the latent heat of fusion. L f = 334 kJ/kg for water, so that
(15.63)
Q = (1.00 kg)(334 kJ/kg) = 3.34×105 J.
Now the change in entropy is positive, since heat transfer occurs into the ice to cause the phase change; thus,
(15.64)
Δ S = QT = 3.34×105 J
T
.
CHAPTER 15 | THERMODYNAMICS 535
T is the melting temperature of ice. That is, T = 0ºC=273 K . So the change in entropy is
(15.65)
Δ S = 3.34 × 105 J
273 K
= 1.22 × 103 J/K.
Discussion
This is a significant increase in entropy accompanying an increase in disorder.
Figure 15.36 When ice melts, it becomes more disordered and less structured. The systematic arrangement of molecules in a crystal structure is replaced by a more random
and less orderly movement of molecules without fixed locations or orientations. Its entropy increases because heat transfer occurs into it. Entropy is a measure of disorder.
In another easily imagined example, suppose we mix equal masses of water originally at two different temperatures, say 20.0º C and 40.0º C . The
result is water at an intermediate temperature of 30.0º C . Three outcomes have resulted: entropy has increased, some energy has become
unavailable to do work, and the system has become less orderly. Let us think about each of these results.
First, entropy has increased for the same reason that it did in the example above. Mixing the two bodies of water has the same effect as heat transfer
from the hot one and the same heat transfer into the cold one. The mixing decreases the entropy of the hot water but increases the entropy of the
cold water by a greater amount, producing an overall increase in entropy.
Second, once the two masses of water are mixed, there is only one temperature—you cannot run a heat engine with them. The energy that could
have been used to run a heat engine is now unavailable to do work.
Third, the mixture is less orderly, or to use another term, less structured. Rather than having two masses at different temperatures and with different
distributions of molecular speeds, we now have a single mass with a uniform temperature.
These three results—entropy, unavailability of energy, and disorder—are not only related but are in fact essentially equivalent.
Life, Evolution, and the Second Law of Thermodynamics
Some people misunderstand the second law of thermodynamics, stated in terms of entropy, to say that the process of the evolution of life violates this
law. Over time, complex organisms evolved from much simpler ancestors, representing a large decrease in entropy of the Earth’s biosphere. It is a
fact that living organisms have evolved to be highly structured, and much lower in entropy than the substances from which they grow. But it is always
possible for the entropy of one part of the universe to decrease, provided the total change in entropy of the universe increases. In equation form, we
can write this as
(15.66)
Δ S tot = Δ S syst + Δ S envir > 0.
Thus Δ S syst can be negative as long as Δ S envir is positive and greater in magnitude.
How is it possible for a system to decrease its entropy? Energy transfer is necessary. If I pick up marbles that are scattered about the room and put
them into a cup, my work has decreased the entropy of that system. If I gather iron ore from the ground and convert it into steel and build a bridge,
my work has decreased the entropy of that system. Energy coming from the Sun can decrease the entropy of local systems on Earth—that is,
Δ S syst is negative. But the overall entropy of the rest of the universe increases by a greater amount—that is, Δ S envir is positive and greater in
magnitude. Thus, Δ S tot = Δ S syst + Δ S envir > 0 , and the second law of thermodynamics is not violated.
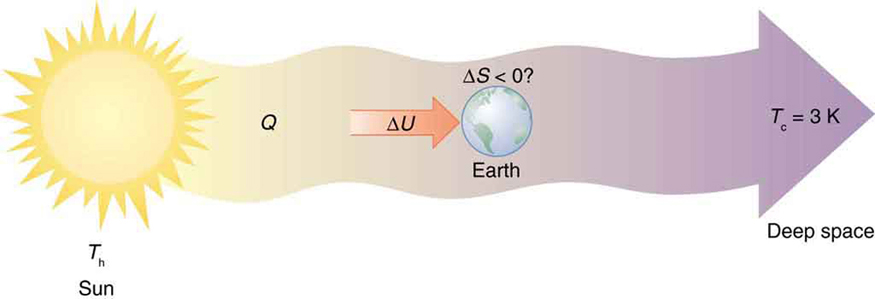
Every time a plant stores some solar energy in the form of chemical potential energy, or an updraft of warm air lifts a soaring bird, the Earth can be
viewed as a heat engine operating between a hot reservoir supplied by the Sun and a cold reservoir supplied by dark outer space—a heat engine of
high complexity, causing local decreases in entropy as it uses part of the heat transfer from the Sun into deep space. There is a large total increase in
entropy resulting from this massive heat transfer. A small part of this heat transfer is stored in structured systems on Earth, producing much smaller
local decreases in entropy. (See Figure 15.37.)


536 CHAPTER 15 | THERMODYNAMICS
Figure 15.37 Earth’s entropy may decrease in the process of intercepting a small part of the heat transfer from the Sun into deep space. Entropy for the entire process
increases greatly while Earth becomes more structured with living systems and stored energy in various forms.
PhET Explorations: Reversible Reactions
Watch a reaction proceed over time. How does total energy affect a reaction rate? Vary temperature, barrier height, and potential energies.
Record concentrations and time in order to extract rate coefficients. Do temperature dependent studies to extract Arrhenius parameters. This
simulation is best used with teacher guidance because it presents an analogy of chemical reactions.
Figure 15.38 Reversible Reactions (http://cnx.org/content/m42237/1.5/reversible-reactions_en.jar)
15.7 Statistical Interpretation of Entropy and the Second Law of Thermodynamics: The
Underlying Explanation
Figure 15.39 When you toss a coin a large number of times, heads and tails tend to come up in roughly equal numbers. Why doesn’t heads come up 100, 90, or even 80% of
the time? (credit: Jon Sullivan, PDPhoto.org)
The various ways of formulating the second law of thermodynamics tell what happens rather than why it happens. Why should heat transfer occur
only from hot to cold? Why should energy become ever less available to do work? Why should the universe become increasingly disorderly? The
answer is that it is a matter of overwhelming probability. Disorder is simply vastly more likely than order.
When you watch an emerging rain storm begin to wet the ground, you will notice that the drops fall in a disorganized manner both in time and in
space. Some fall close together, some far apart, but they never fall in straight, orderly rows. It is not impossible for rain to fall in an orderly pattern, just
highly unlikely, because there are many more disorderly ways than orderly ones. To illustrate this fact, we will examine some random processes,
starting with coin tosses.
Coin Tosses
What are the possible outcomes of tossing 5 coins? Each coin can land either heads or tails. On the large scale, we are concerned only with the total
heads and tails and not with the order in which heads and tails appear. The following possibilities exist:
CHAPTER 15 | THERMODYNAMICS 537
(15.67)
5 heads, 0 tails
4 heads, 1 tail
3 heads, 2 tails
2 heads, 3 tails
1 head, 4 tails
0 head, 5 tails
These are what we call macrostates. A macrostate is an overall property of a system. It does not specify the details of the system, such as the order
in which heads and tails occur or which coins are heads or tails.
Using this nomenclature, a system of 5 coins has the 6 possible macrostates just listed. Some macrostates are more likely to occur than others. For
instance, there is only one way to get 5 heads, but there are several ways to get 3 heads and 2 tails, making the latter macrostate more probable.
Table 15.3 lists of all the ways in which 5 coins can be tossed, taking into account the order in which heads and tails occur. Each sequence is called a microstate—a detailed description of every element of a system.
Table 15.3 5-Coin Toss
Individual microstates
Number of microstates
5 heads, 0 tails HHHHH
1
4 heads, 1 tail HHHHT, HHHTH, HHTHH, HTHHH, THHHH
5
3 heads, 2 tails HTHTH, THTHH, HTHHT, THHTH, THHHT HTHTH, THTHH, HTHHT, THHTH, THHHT
10
2 heads, 3 tails TTTHH, TTHHT, THHTT, HHTTT, TTHTH, THTHT, HTHTT, THTTH, HTTHT, HTTTH
10
1 head, 4 tails TTTTH, TTTHT, TTHTT, THTTT, HTTTT
5
0 heads, 5 tails TTTTT
1
Total: 32
The macrostate of 3 heads and 2 tails can be achieved in 10 ways and is thus 10 times more probable than the one having 5 heads. Not surprisingly,
it is equally probable to have the reverse, 2 heads and 3 tails. Similarly, it is equally probable to get 5 tails as it is to get 5 heads. Note that all of these
conclusions are based on the crucial assumption that each microstate is equally probable. With coin tosses, this requires that the coins not be
asymmetric in a way that favors one side over the other, as with loaded dice. With any system, the assumption that all microstates are equally
probable must be valid, or the analysis will be erroneous.
The two most orderly possibilities are 5 heads or 5 tails. (They are more structured than the others.) They are also the least likely, only 2 out of 32
possibilities. The most disorderly possibilities are 3 heads and 2 tails and its reverse. (They are the least structured.) The most disorderly possibilities
are also the most likely, with 20 out of 32 possibilities for the 3 heads and 2 tails and its reverse. If we start with an orderly array like 5 heads and toss
the coins, it is very likely that we will get a less orderly array as a result, since 30 out of the 32 possibilities are less orderly. So even if you start with
an orderly state, there is a strong tendency to go from order to disorder, from low entropy to high entropy. The reverse can happen, but it is unlikely.
538 CHAPTER 15 | THERMODYNAMICS
Table 15.4 100-Coin Toss
Macrostate
Number of microstates
Heads
Tails
( W)
100
0
1
99
1
1.0 × 102
95
5
7.5 × 107
90
10
1.7 × 1013
75
25
2.4 × 1023
60
40
1.4 × 1028
55
45
6.1 × 1028
51
49
9.9 × 1028
50
50
1.0 × 1029
49
51
9.9 × 1028
45
55
6.1 × 1028
40
60
1.4 × 1028
25
75
2.4 × 1023
10
90
1.7 × 1013
5
95
7.5 × 107
1
99
1.0 × 102
0
100
1
Total: 1.27 × 1030
This result becomes dramatic for larger systems. Consider what happens if you have 100 coins instead of just 5. The most orderly arrangements
(most structured) are 100 heads or 100 tails. The least orderly (least structured) is that of 50 heads and 50 tails. There is only 1 way (1 microstate) to
get the most orderly arrangement of 100 heads. There are 100 ways (100 microstates) to get the next most orderly arrangement of 99 heads and 1
tail (also 100 to get its reverse). And there are 1.0×1029 ways to get 50 heads and 50 tails, the least orderly arrangement. Table 15.4 is an
abbreviated list of the various macrostates and the number of microstates for each macrostate. The total number of microstates—the total number of
different ways 100 coins can be tossed—is an impressively large 1.27×1030 . Now, if we start with an orderly macrostate like 100 heads and toss
the coins, there is a virtual certainty that we will get a less orderly macrostate. If we keep tossing the coins, it is possible, but exceedingly unlikely, that
we will ever get back to the most orderly macrostate. If you tossed the coins once each second, you could expect to get either 100 heads or 100 tails
once in 2×1022 years! This period is 1 trillion ( 1012 ) times longer than the age of the universe, and so the chances are essentially zero. In
contrast, there is an 8% chance of getting 50 heads, a 73% chance of getting from 45 to 55 heads, and a 96% chance of getting from 40 to 60 heads.
Disorder is highly likely.
Disorder in a Gas
The fantastic growth in the odds favoring disorder that we see in going from 5 to 100 coins continues as the number of entities in the system
increases. Let us now imagine applying this approach to perhaps a small sample of gas. Because counting microstates and macrostates involves
statistics, this is called statistical analysis. The macrostates of a gas correspond to its macroscopic properties, such as volume, temperature, and
pressure; and its microstates correspond to the detailed description of the positions and velocities of its atoms. Even a small amount of gas has a
huge number of atoms: 1.0 cm3 of an ideal gas at 1.0 atm and 0º C has 2.7×1019 atoms. So each macrostate has an immense number of
microstates. In plain language, this means that there are an immense number of ways in which the atoms in a gas can be arranged, while still having
the same pressure, temperature, and so on.
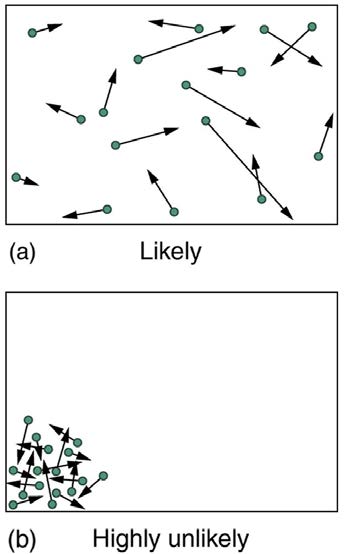
The most likely conditions (or macrostates) for a gas are those we see all the time—a random distribution of atoms in space with a Maxwell-
Boltzmann distribution of speeds in random directions, as predicted by kinetic theory. This is the most disorderly and least structured condition we
can imagine. In contrast, one type of very orderly and structured macrostate has all of the atoms in one corner of a container with identical velocities.
There are very few ways to accomplish this (very few microstates corresponding to it), and so it is exceedingly unlikely ever to occur. (See Figure
15.40(b).) Indeed, it is so unlikely that we have a law saying that it is impossible, which has never been observed to be violated—the second law of thermodynamics.
CHAPTER 15 | THERMODYNAMICS 539
Figure 15.40 (a) The ordinary state of gas in a container is a disorderly, random distribution of atoms or molecules with a Maxwell-Boltzmann distribution of speeds. It is so
unlikely that these atoms or molecules would ever end up in one corner of the container that it might as well be impossible. (b) With energy transfer, the gas can be forced into
one corner and its entropy greatly reduced. But left alone, it will spontaneously increase its entropy and return to the normal conditions, because they are immensely more
likely.
The disordered condition is one of high entropy, and the ordered one has low entropy. With a transfer of energy from another system, we could force
all of the atoms into one corner and have a local decrease in entropy, but at the cost of an overall increase in entropy of the universe. If the atoms
start out in one corner, they will quickly disperse and become uniformly distributed and will never return to the orderly original state (Figure 15.40(b)).
Entropy will increase. With such a large sample of atoms, it is possible—but unimaginably unlikely—for entropy to decrease. Disorder is vastly more
likely than order.
The arguments that disorder and high entropy are the most probable states are quite convincing. The great Austrian physicist Ludwig Boltzmann
(1844–1906)—who, along with Maxwell, made so many contributions to kinetic theory—proved that the entropy of a system in a given state (a
macrostate) can be written as
S
(15.68)
= k ln W,
where k = 1.38×10−23 J/K is Boltzmann’s constant, and ln W is the natural logarithm of the number of microstates W corresponding to the
given macrostate. W is proportional to the probability that the macrostate will occur. Thus entropy is directly related to the probability of a state—the
more likely the state, the greater its entropy. Boltzmann proved that this expression for S is equivalent to the definition Δ S = Q / T , which we have used extensively.
Thus the second law of thermodynamics is explained on a very basic level: entropy either remains the same or increases in every process. This
phenomenon is due to the extraordinarily small probability of a decrease, based on the extraordinarily larger number of microstates in systems with
greater entropy. Entropy can decrease, but for any macroscopic system, this outcome is so unlikely that it will never be observed.
Example 15.9 Entropy Increases in a Coin Toss
Suppose you toss 100 coins starting with 60 heads and 40 tails, and you get the most likely result, 50 heads and 50 tails. What is the change in
entropy?
Strategy
Noting that the number of microstates is labeled W in Table 15.4 for the 100-coin toss, we can use Δ S = S f − S i = k ln W f - k ln W i to calculate the change in entropy.
Solution
The change in entropy is
(15.69)
Δ S = S f – S i = k ln W f – k ln W i,
where the subscript i stands for the initial 60 heads and 40 tails state, and the subscript f for the final 50 heads and 50 tails state. Substituting the
values for W from Table 15.4 gives
(15.70)
Δ S = (1.38×10 – 23 J/K)[ln(1.0×1029 ) – ln(1.4×1028)]
= 2.7×10 – 23 J/K
540 CHAPTER 15 | THERMODYNAMICS
Discussion
This increase in entropy means we have moved to a less orderly situation. It is not impossible for further tosses to produce the initial state of 60
heads and 40 tails, but it is less likely. There is about a 1 in 90 chance for that decrease in entropy ( – 2.7×10 – 23 J/K ) to occur. If we
calculate the decrease in entropy to move to the most orderly state, we get Δ S = – 92×10 – 23 J/K . There is about a 1 in 1030 chance of
this change occurring. So while very small decreases in entropy are unlikely, slightly greater decreases are impossibly unlikely. These
probabilities imply, again, that for a macroscopic system, a decrease in entropy is impossible. For example, for heat transfer to occur
spontaneously from 1.00 kg of 0ºC ice to its 0ºC environment, there would be a decrease in entropy of 1.22×103 J/K . Given that a
Δ S of 10 – 21 J/K corresponds to about a 1 in 1030 chance, a decrease of this size ( 103 J/K ) is an utter impossibility. Even for a milligram
of melted ice to spontaneously refreeze is impossible.
Problem-Solving Strategies for Entropy
1. Examine the situation to determine if entropy is involved.
2. Identify the system of interest and draw a labeled diagram of the system showing energy flow.
3. Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful.
4. Make a list of what is given or can be inferred from the problem as stated (identify the knowns). You must carefully identify the heat transfer,
if any, and the temperature at which the process takes place. It is also important to identify the initial and final states.
5. Solve the appropriate equation for the quantity to be determined (the unknown). Note that the change in entropy can be determined
between any states by calculating it for a reversible process.
6. Substitute the known value along with their units into the appropriate equation, and obtain numerical solutions complete with units.
7. To see if it is reasonable: Does it make sense? For example, total entropy should increase for any real process or be constant for a
reversible process. Disordered states should be more probable and have greater entropy than ordered states.
Glossary
adiabatic process: a process in which no heat transfer takes place
Carnot cycle: a cyclical process that uses only reversible processes, the adiabatic and isothermal processes
Carnot efficiency: the maximum theoretical efficiency for a heat engine
Carnot engine: a heat engine that uses a Carnot cycle
change in entropy: the ratio of heat transfer to temperature Q / T
coefficient of performance: for a heat pump, it is the ratio of heat transfer at the output (the hot reservoir) to the work supplied; for a refrigerator
or air conditioner, it is the ratio of heat transfer from the cold reservoir to the work








