example, the fact that, at body temperature, perspiration from the skin requires a heat input of 2428 kJ/kg, which is about 10 percent higher than the
latent heat of vaporization at 100ºC . This heat comes from the skin, and thus provides an effective cooling mechanism in hot weather. High humidity
inhibits evaporation, so that body temperature might rise, leaving unevaporated sweat on your brow.
Example 14.4 Calculate Final Temperature from Phase Change: Cooling Soda with Ice Cubes
Three ice cubes are used to chill a soda at 20ºC with mass m soda = 0.25 kg . The ice is at 0ºC and each ice cube has a mass of 6.0 g.
Assume that the soda is kept in a foam container so that heat loss can be ignored. Assume the soda has the same heat capacity as water. Find
the final temperature when all ice has melted.
Strategy
The ice cubes are at the melting temperature of 0ºC . Heat is transferred from the soda to the ice for melting. Melting of ice occurs in two steps:
first the phase change occurs and solid (ice) transforms into liquid water at the melting temperature, then the temperature of this water rises.
Melting yields water at 0ºC , so more heat is transferred from the soda to this water until the water plus soda system reaches thermal
equilibrium,
Q
(14.19)
ice = − Q soda.
The heat transferred to the ice is Q ice = m ice L f + m ice c W( T f − 0ºC) . The heat given off by the soda is Q soda = m soda c W( T f − 20ºC) .
Since no heat is lost, Q ice = − Q soda , so that
⎛
⎛
(14.20)
m ice L f + m ice c W⎝ T f − 0ºC⎞⎠ = - m soda c W⎝ T f − 20ºC⎞⎠.
Bring all terms involving T f on the left-hand-side and all other terms on the right-hand-side. Solve for the unknown quantity T f :
(14.21)
T f = m soda c W(20ºC) − m ice L f
( m
.
soda + m ice) c W
Solution
1. Identify the known quantities. The mass of ice is m ice = 3×6.0 g = 0.018 kg and the mass of soda is m soda = 0.25 kg .
2. Calculate the terms in the numerator:
⎛
(14.22)
m soda c W(20ºC) = ⎛⎝0.25 kg⎞⎠⎝4186 J/kg⋅ºC⎞⎠(20ºC) = 20,930 J
and
⎛
(14.23)
m ice L f = ⎛⎝0.018 kg⎞⎠⎝334,000 J/kg⎞⎠=6012 J.
3. Calculate the denominator:
⎛
(14.24)
( m soda + m ice) c W = ⎛⎝0.25 kg + 0.018 kg⎞⎠⎝4186 K/(kg⋅ºC⎞⎠=1122 J/ºC.
4. Calculate the final temperature:
(14.25)
T f = 20 , 930 J − 6012 J
1122 J/ºC
= 13ºC.
Discussion
This example illustrates the enormous energies involved during a phase change. The mass of ice is about 7 percent the mass of water but leads
to a noticeable change in the temperature of soda. Although we assumed that the ice was at the freezing temperature, this is incorrect: the
typical temperature is −6ºC . However, this correction gives a final temperature that is essentially identical to the result we found. Can you
explain why?
We have seen that vaporization requires heat transfer to a liquid from the surroundings, so that energy is released by the surroundings.
Condensation is the reverse process, increasing the temperature of the surroundings. This increase may seem surprising, since we associate
condensation with cold objects—the glass in the figure, for example. However, energy must be removed from the condensing molecules to make a
vapor condense. The energy is exactly the same as that required to make the phase change in the other direction, from liquid to vapor, and so it can
be calculated from Q = mL v .


480 CHAPTER 14 | HEAT AND HEAT TRANSFER METHODS
Figure 14.9 Condensation forms on this glass of iced tea because the temperature of the nearby air is reduced to below the dew point. The air cannot hold as much water as it
did at room temperature, and so water condenses. Energy is released when the water condenses, speeding the melting of the ice in the glass. (credit: Jenny Downing)
Real-World Application
Energy is also released when a liquid freezes. This phenomenon is used by fruit growers in Florida to protect oranges when the temperature is
close to the freezing point (0ºC) . Growers spray water on the plants in orchards so that the water freezes and heat is released to the growing
oranges on the trees. This prevents the temperature inside the orange from dropping below freezing, which would damage the fruit.
Figure 14.10 The ice on these trees released large amounts of energy when it froze, helping to prevent the temperature of the trees from dropping below 0ºC . Water is
intentionally sprayed on orchards to help prevent hard frosts. (credit: Hermann Hammer)
Sublimation is the transition from solid to vapor phase. You may have noticed that snow can disappear into thin air without a trace of liquid water, or
the disappearance of ice cubes in a freezer. The reverse is also true: Frost can form on very cold windows without going through the liquid stage. A
popular effect is the making of “smoke” from dry ice, which is solid carbon dioxide. Sublimation occurs because the equilibrium vapor pressure of
solids is not zero. Certain air fresheners use the sublimation of a solid to inject a perfume into the room. Moth balls are a slightly toxic example of a
phenol (an organic compound) that sublimates, while some solids, such as osmium tetroxide, are so toxic that they must be kept in sealed containers
to prevent human exposure to their sublimation-produced vapors.

CHAPTER 14 | HEAT AND HEAT TRANSFER METHODS 481
Figure 14.11 Direct transitions between solid and vapor are common, sometimes useful, and even beautiful. (a) Dry ice sublimates directly to carbon dioxide gas. The visible
vapor is made of water droplets. (credit: Windell Oskay) (b) Frost forms patterns on a very cold window, an example of a solid formed directly from a vapor. (credit: Liz West)
All phase transitions involve heat. In the case of direct solid-vapor transitions, the energy required is given by the equation Q = mL s , where L s is
the heat of sublimation, which is the energy required to change 1.00 kg of a substance from the solid phase to the vapor phase. L s is analogous to
L f and L v , and its value depends on the substance. Sublimation requires energy input, so that dry ice is an effective coolant, whereas the reverse
process (i.e., frosting) releases energy. The amount of energy required for sublimation is of the same order of magnitude as that for other phase
transitions.
The material presented in this section and the preceding section allows us to calculate any number of effects related to temperature and phase
change. In each case, it is necessary to identify which temperature and phase changes are taking place and then to apply the appropriate equation.
Keep in mind that heat transfer and work can cause both temperature and phase changes.
Problem-Solving Strategies for the Effects of Heat Transfer
1. Examine the situation to determine that there is a change in the temperature or phase. Is there heat transfer into or out of the system? When
the presence or absence of a phase change is not obvious, you may wish to first solve the problem as if there were no phase changes, and
examine the temperature change obtained. If it is sufficient to take you past a boiling or melting point, you should then go back and do the
problem in steps—temperature change, phase change, subsequent temperature change, and so on.
2. Identify and list all objects that change temperature and phase.
3. Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful.
4. Make a list of what is given or what can be inferred from the problem as stated (identify the knowns).
5. Solve the appropriate equation for the quantity to be determined (the unknown). If there is a temperature change, the transferred heat depends
on the specific heat (see Table 14.1) whereas, for a phase change, the transferred heat depends on the latent heat. See Table 14.2.
6. Substitute the knowns along with their units into the appropriate equation and obtain numerical solutions complete with units. You will need to
do this in steps if there is more than one stage to the process (such as a temperature change followed by a phase change).
7. Check the answer to see if it is reasonable: Does it make sense? As an example, be certain that the temperature change does not also cause a
phase change that you have not taken into account.
Check Your Understanding
Why does snow remain on mountain slopes even when daytime temperatures are higher than the freezing temperature?
Solution
Snow is formed from ice crystals and thus is the solid phase of water. Because enormous heat is necessary for phase changes, it takes a certain
amount of time for this heat to be accumulated from the air, even if the air is above 0ºC . The warmer the air is, the faster this heat exchange
occurs and the faster the snow melts.
14.4 Heat Transfer Methods
Equally as interesting as the effects of heat transfer on a system are the methods by which this occurs. Whenever there is a temperature difference,
heat transfer occurs. Heat transfer may occur rapidly, such as through a cooking pan, or slowly, such as through the walls of a picnic ice chest. We
can control rates of heat transfer by choosing materials (such as thick wool clothing for the winter), controlling air movement (such as the use of
weather stripping around doors), or by choice of color (such as a white roof to reflect summer sunlight). So many processes involve heat transfer, so
that it is hard to imagine a situation where no heat transfer occurs. Yet every process involving heat transfer takes place by only three methods:
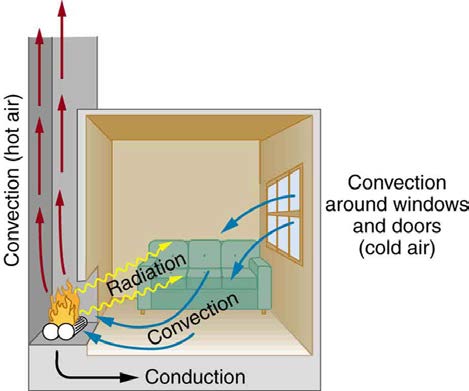

482 CHAPTER 14 | HEAT AND HEAT TRANSFER METHODS
1. Conduction is heat transfer through stationary matter by physical contact. (The matter is stationary on a macroscopic scale—we know there is
thermal motion of the atoms and molecules at any temperature above absolute zero.) Heat transferred between the electric burner of a stove
and the bottom of a pan is transferred by conduction.
2. Convection is the heat transfer by the macroscopic movement of a fluid. This type of transfer takes place in a forced-air furnace and in weather
systems, for example.
3. Heat transfer by radiation occurs when microwaves, infrared radiation, visible light, or another form of electromagnetic radiation is emitted or
absorbed. An obvious example is the warming of the Earth by the Sun. A less obvious example is thermal radiation from the human body.
Figure 14.12 In a fireplace, heat transfer occurs by all three methods: conduction, convection, and radiation. Radiation is responsible for most of the heat transferred into the room. Heat transfer also occurs through conduction into the room, but at a much slower rate. Heat transfer by convection also occurs through cold air entering the room around
windows and hot air leaving the room by rising up the chimney.
We examine these methods in some detail in the three following modules. Each method has unique and interesting characteristics, but all three do
have one thing in common: they transfer heat solely because of a temperature difference Figure 14.12.
Check Your Understanding
Name an example from daily life (different from the text) for each mechanism of heat transfer.
Solution
Conduction: Heat transfers into your hands as you hold a hot cup of coffee.
Convection: Heat transfers as the barista “steams” cold milk to make hot cocoa.
Radiation: Reheating a cold cup of coffee in a microwave oven.
14.5 Conduction
Figure 14.13 Insulation is used to limit the conduction of heat from the inside to the outside (in winters) and from the outside to the inside (in summers). (credit: Giles Douglas) Your feet feel cold as you walk barefoot across the living room carpet in your cold house and then step onto the kitchen tile floor. This result is
intriguing, since the carpet and tile floor are both at the same temperature. The different sensation you feel is explained by the different rates of heat
transfer: the heat loss during the same time interval is greater for skin in contact with the tiles than with the carpet, so the temperature drop is greater
on the tiles.
Some materials conduct thermal energy faster than others. In general, good conductors of electricity (metals like copper, aluminum, gold, and silver)
are also good heat conductors, whereas insulators of electricity (wood, plastic, and rubber) are poor heat conductors. Figure 14.14 shows molecules
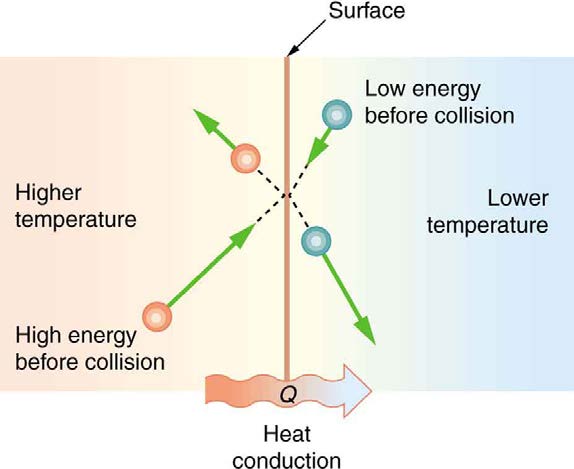
CHAPTER 14 | HEAT AND HEAT TRANSFER METHODS 483
in two bodies at different temperatures. The (average) kinetic energy of a molecule in the hot body is higher than in the colder body. If two molecules
collide, an energy transfer from the hot to the cold molecule occurs. The cumulative effect from all collisions results in a net flux of heat from the hot
body to the colder body. The heat flux thus depends on the temperature difference Δ Τ = Τ hot − T cold . Therefore, you will get a more severe burn
from boiling water than from hot tap water. Conversely, if the temperatures are the same, the net heat transfer rate falls to zero, and equilibrium is
achieved. Owing to the fact that the number of collisions increases with increasing area, heat conduction depends on the cross-sectional area. If you
touch a cold wall with your palm, your hand cools faster than if you just touch it with your fingertip.
Figure 14.14 The molecules in two bodies at different temperatures have different average kinetic energies. Collisions occurring at the contact surface tend to transfer energy
from high-temperature regions to low-temperature regions. In this illustration, a molecule in the lower temperature region (right side) has low energy before collision, but its
energy increases after colliding with the contact surface. In contrast, a molecule in the higher temperature region (left side) has high energy before collision, but its energy
decreases after colliding with the contact surface.
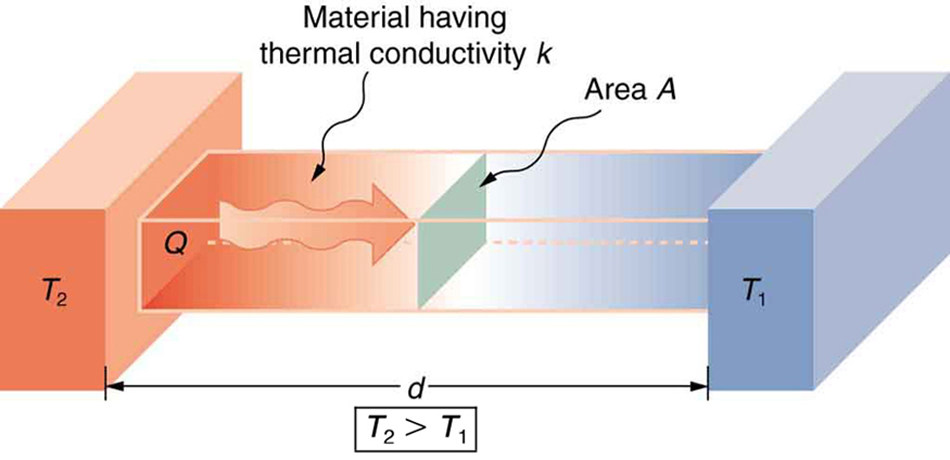
A third factor in the mechanism of conduction is the thickness of the material through which heat transfers. The figure below shows a slab of material
with different temperatures on either side. Suppose that T 2 is greater than T 1 , so that heat is transferred from left to right. Heat transfer from the
left side to the right side is accomplished by a series of molecular collisions. The thicker the material, the more time it takes to transfer the same
amount of heat. This model explains why thick clothing is warmer than thin clothing in winters, and why Arctic mammals protect themselves with thick
blubber.
Figure 14.15 Heat conduction occurs through any material, represented here by a rectangular bar, whether window glass or walrus blubber. The temperature of the material is
T 2 on the left and T 1 on the right, where T 2 is greater than T 1 . The rate of heat transfer by conduction is directly proportional to the surface area A , the temperature difference T 2 − T 1 , and the substance’s conductivity k . The rate of heat transfer is inversely proportional to the thickness d .
Lastly, the heat transfer rate depends on the material properties described by the coefficient of thermal conductivity. All four factors are included in a
simple equation that was deduced from and is confirmed by experiments. The rate of conductive heat transfer through a slab of material, such as
the one in Figure 14.15, is given by
(14.26)
Qt = kA( T 2− T 1)
d
,
where Q / t is the rate of heat transfer in watts or kilocalories per second, k is the thermal conductivity of the material, A and d are its surface area and thickness, as shown in Figure 14.15, and ( T 2 − T 1) is the temperature difference across the slab. Table 14.3 gives representative values of thermal conductivity.
484 CHAPTER 14 | HEAT AND HEAT TRANSFER METHODS
Example 14.5 Calculating Heat Transfer Through Conduction: Conduction Rate Through an Ice Box
A Styrofoam ice box has a total area of 0.950 m2 and walls with an average thickness of 2.50 cm. The box contains ice, water, and canned
beverages at 0ºC . The inside of the box is kept cold by melting ice. How much ice melts in one day if the ice box is kept in the trunk of a car at
35.0ºC ?
Strategy
This question involves both heat for a phase change (melting of ice) and the transfer of heat by conduction. To find the amount of ice melted, we
must find the net heat transferred. This value can be obtained by calculating the rate of heat transfer by conduction and multiplying by time.
Solution
1. Identify the knowns.
(14.27)
A = 0.950 m2 ; d = 2.50 cm = 0.0250 m; T 1 = 0ºC; T 2 = 35.0ºC, t = 1 day = 24 hours = 86,400 s.
2. Identify the unknowns. We need to solve for the mass of the ice, m . We will also need to solve for the net heat transferred to melt the ice,
Q .
3. Determine which equations to use. The rate of heat transfer by conduction is given by
(14.28)
Qt = kA( T 2− T 1)
d
.
4. The heat is used to melt the ice: Q = mL f.
5. Insert the known values:
(14.29)
Q
(0.010 J/s ⋅ m⋅ºC)⎛⎝0.950 m2⎞⎠(35.0ºC − 0ºC)
t =
0.0250 m
= 13.3 J/s.
6. Multiply the rate of heat transfer by the time ( 1 day = 86,400 s ):
(14.30)
Q = ⎛⎝ Q / t⎞⎠ t = (13.3 J/s)(86 , 400 s) = 1.15×106 J.
7. Set this equal to the heat transferred to melt the ice: Q = mL f . Solve for the mass m :
(14.31)
m = Q
L = 1.15×106 J = 3.44kg.
f
334 ×103 J/kg
Discussion
The result of 3.44 kg, or about 7.6 lbs, seems about right, based on experience. You might expect to use about a 4 kg (7–10 lb) bag of ice per
day. A little extra ice is required if you add any warm food or beverages.
Inspecting the conductivities in Table 14.3 shows that Styrofoam is a very poor conductor and thus a good insulator. Other good insulators
include fiberglass, wool, and goose-down feathers. Like Styrofoam, these all incorporate many small pockets of air, taking advantage of air’s
poor thermal conductivity.

CHAPTER 14 | HEAT AND HEAT TRANSFER METHODS 485
Table 14.3 Thermal Conductivities of Common Substances[7]
Substance
Thermal conductivity k (J/s⋅m⋅ºC)
Silver
420
Copper
390
Gold
318
Aluminum
220
Steel iron
80
Steel (stainless)
14
Ice
2.2
Glass (average)
0.84
Concrete brick
0.84
Water
0.6
Fatty tissue (without blood)
0.2
Asbestos
0.16
Plasterboard
0.16
Wood
0.08–0.16
Snow (dry)
0.10
Cork
0.042
Glass wool
0.042
Wool
0.04
Down feathers
0.025
Air
0.023
Styrofoam
0.010
A combination of material and thickness is often manipulated to develop good insulators—the smaller the conductivity k and the larger the thickness
d , the better. The ratio of d / k will thus be large for a good insulator. The ratio d / k is called the R factor. The rate of conductive heat transfer is inversely proportional to R . The larger the value of R , the better the insulation. R factors are most commonly quoted for household insulation,
refrigerators, and the like—unfortunately, it is still in non-metric units of ft2·°F·h/Btu, although the unit usually goes unstated (1 British thermal unit
[Btu] is the amount of energy needed to change the temperature of 1.0 lb of water by 1.0 °F). A couple of representative values are an R factor of 11
for 3.5-in-thick fiberglass batts (pieces) of insulation and an R factor of 19 for 6.5-in-thick fiberglass batts. Walls are usually insulated with 3.5-in
batts, while ceilings are usually insulated with 6.5-in batts. In cold climates, thicker batts may be used in ceilings and walls.
Figure 14.16 The fiberglass batt is used for insulation of walls and ceilings to prevent heat transfer between the inside of the building and the outside environment.
Note that in Table 14.3, the best thermal conductors—silver, copper, gold, and aluminum—are also the best electrical conductors, again related to the density of free electrons in them. Cooking utensils are typically made from good conductors.
Example 14.6 Calculating the Temperature Difference Maintained by a Heat Transfer: Conduction Through an
Aluminum Pan
Water is boiling in an aluminum pan placed on an electrical element on a stovetop. The sauce pan has a bottom that is 0.800 cm thick and 14.0
cm in diameter. The boiling water is evaporating at the rate of 1.00 g/s. What is the temperature difference across (through) the bottom of the
pan?
Strategy
Conduction through the aluminum is the primary method of heat transfer here, and so we use the equation for the rate of heat transfer and solve
for the temperature difference.
7. At temperatures near 0ºC.
486 CHAPTER 14 | HEAT AND HEAT TRANSFER METHODS
(14.32)
T
⎛ d ⎞
2 − T 1 = Qt⎝ kA⎠.
Solution











