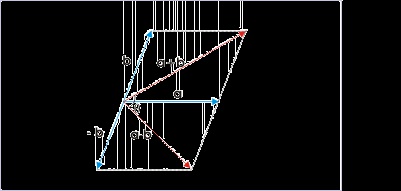
From graphical representation, the angle that vector makes with y-axis has following
trigonometric function :
Figure 1.58. Angle
Vector makes an angle with y-axis.
Now, we apply the formulae to find the angle, say θ, with y-axis,
In case, we are only interested to know the magnitude of angle between vector and y-axis, then we
can neglect the negative sign,
Exercise 11.
If a vector makes angles α,β and γ with x,y and z axes of a rectangular coordinate system, then
prove that :
The vector can be expressed in terms of its component as :
where
.
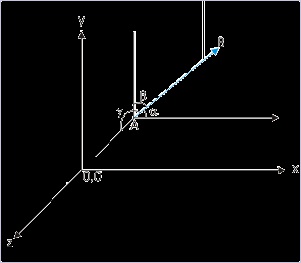




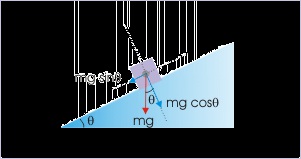
Figure 1.58. Angles
Vector makes different angles with axes..
The magnitude of the vector is given by :
Putting expressions of components in the equation,
Squaring both sides,
Exercise 12.
Find the components of weight of a block along the incline and perpendicular to the incline.
The component of the weight along the incline is :
Figure 1.58. Weight on an incline






Components of weight along the incline and perpendicualt to the incline.
and the component of weight perpendicular to incline is :
Exercise 13.
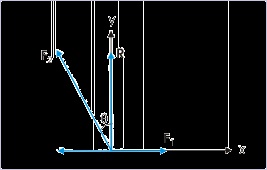
The sum of magnitudes of two forces acting at a point is 16 N. If the resultant of the two forces is
8 N and it is normal to the smaller of the two forces, then find the forces.
We depict the situation as shown in the figure. The resultant force R is shown normal to small
force F 1 . In order that the sum of the forces is equal to R, the component of larger force along the
x-direction should be equal to smaller force :
Figure 1.58. Two forces acting on a point
The resultant force is perpendicular to smaller of the two forces.
Also, the component of the larger force along y-direction should be equal to the magnitude of
resultant,
Squaring and adding two equations, we have :
However, according to the question,



Substituting, we have :
Solving,
More illustrations on the subject are available in the module titled Resolution of forces
1.8. Scalar (dot) product*
In physics, we require to multiply a vector with other scalar and vector quantities. The vector
multiplication, however, is not an unique mathematical construct like scalar multiplication. The
multiplication depends on the nature of quantities (vector or scalar) and on the physical process,
necessitating scalar or vector multiplication.
The rules of vector multiplication have been formulated to encapsulate physical processes in their
completeness. This is the core consideration. In order to explore this aspect, let us find out the
direction of acceleration in the case of parabolic motion of a particle. There may be two ways to
deal with the requirement. We may observe the directions of velocities at two points along the
path and find out the direction of the change of velocities. Since we know that the direction of
change of velocity is the direction of acceleration, we draw the vector diagram and find out the
direction of acceleration. We can see that the direction of acceleration turns out to act in vertically
downward direction.
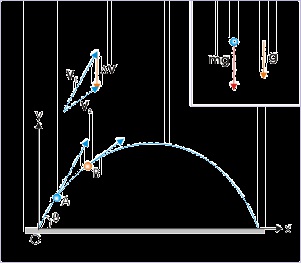


Figure 1.59. Direction of acceleration
The conceptualization of physical laws in vector form, however, provides us with powerful means
to arrive at the result in relatively simpler manner. If we look at the flight of particle in parabolic
motion, then we observe that the motion of particle is under the force of gravity, which is acting
vertically downward. There is no other force (neglecting air resistance). Now, from second law of
motion, we know that :
This equation reveals that the direction of acceleration is same as that of the resultant force acting
on the particle. Thus, acceleration of the particle in parabolic motion is acting vertically
downward. We see that this second approach is more elegant of the two methods. We could arrive
at the correct answer in a very concise manner, without getting into the details of the motion. It is
possible, because Newton's second law in vector form states that net force on the body is product
of acceleration vector with scalar mass. As multiplication of scalar with a vector does not change
the direction of resultant vector, we conclude that direction of acceleration is same as that of net
force acting on the projectile.
Multiplication with scalar
Multiplication of a vector, A, with another scalar quantity, a, results in another vector, B. The
magnitude of the resulting vector is equal to the product of the magnitude of vector with the scalar
quantity. The direction of the resulting vector, however, is same as that of the original vector (See
Figures below).
()
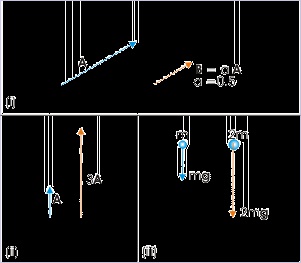


Figure 1.60. Multiplication with scalar
We have already made use of this type of multiplication intuitively in expressing a vector in
component form.
In this vector representation, each component vector is obtained by multiplying the scalar
component with the unit vector. As the unit vector has the magnitude of 1 with a specific
direction, the resulting component vector retains the magnitude of the scalar component, but
acquires the direction of unit vector.
()
Products of vectors
Some physical quantities are themselves a scalar quantity, but are composed from the product of
vector quantities. One such example is “work”. On the other hand, there are physical quantities
like torque and magnetic force on a moving charge, which are themselves vectors and are also
composed from vector quantities.
Thus, products of vectors are defined in two distinct manner – one resulting in a scalar quantity
and the other resulting in a vector quantity. The product that results in scalar value is scalar
product, also known as dot product as a "dot" ( . ) is the symbol of operator for this product. On the
other hand, the product that results in vector value is vector product, also known as cross product
as a "cross" ( x) is the symbol of operator for this product. We shall discuss scalar product only in
this module. We shall cover vector product in a separate module.
Scalar product (dot product)
Scalar product of two vectors a and b is a scalar quantity defined as :

()
where “a” and “b” are the magnitudes of two vectors and “θ” is the angle between the direction of
two vectors. It is important to note that vectors have two angles θ and 2π - θ. We can use either of
them as cosine of both “θ” and “2π - θ” are same. However, it is suggested to use the smaller of
the enclosed angles to be consistent with cross product in which it is required to use the smaller of
the enclosed angles. This approach will maintain consistency with regard to enclosed angle in two
types of vector multiplications.
The notation “ a.b” is important and should be mentally noted to represent a scalar quantity – even
though it involves bold faced vectors. It should be noted that the quantity on the right hand side of
the equation is a scalar.
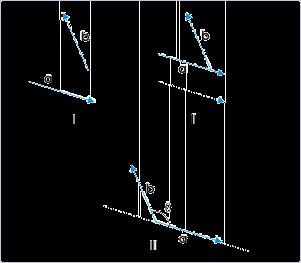
Angle between vectors
The angle between vectors is measured with precaution. The direction of vectors may sometimes
be misleading. The basic consideration is that it is the angle between vectors at the common point
of intersection. This intersection point, however, should be the common tail of vectors. If
required, we may be required to shift the vector parallel to it or along its line of action to obtain
common point at which tails of vectors meet.
Figure 1.61. Angle between vectors
Angle between vectors
See the steps shown in the figure. First, we need to shift one of two vectors say, a so that it
touches the tail of vector b. Second, we move vector a along its line of action till tails of two
vectors meet at the common point. Finally, we measure the angle θ such that 0≤ θ≤π.
Meaning of scalar product
We can read the definition of scalar product in either of the following manners :


()
Recall that “bcos θ” is the scalar component of vector b along the direction of vector a and “a cos
θ” is the scalar component of vector a along the direction of vector b. Thus, we may consider the
scalar product of vectors a and b as the product of the magnitude of one vector and the scalar
component of other vector along the first vector.
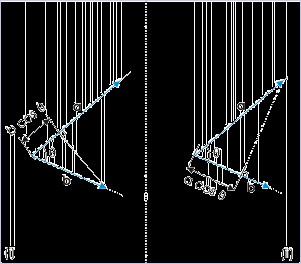
The figure below shows drawing of scalar components. The scalar component of vector in figure
(i) is obtained by drawing perpendicular from the tip of the vector, b, on the direction of vector, a.
Similarly, the scalar component of vector in figure (ii) is obtained by drawing perpendicular from
the tip of the vector, a, on the direction of vector, b.
Figure 1.62. Scalar product
The two alternate ways of evaluating dot product of two vectors indicate that the product is
commutative i.e. independent of the order of two vectors :
()
Exercise 14.
A block of mass “m” moves from point A to B along a smooth plane surface under the action of
force as shown in the figure. Find the work done if it is defined as :
W = F. Δ x
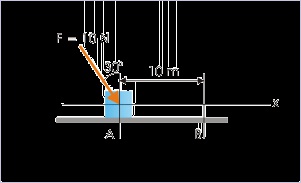
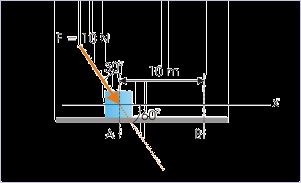




Figure 1.62. Work done
where F and Δ x are force and displacement vectors.
Expanding the expression of work, we have :
Figure 1.62. Work done
Here, F = 10 N, Δx = 10 m and cosθ = cos60° = 0.5.
Values of scalar product
The value of dot product is maximum for the maximum value of cosθ. Now, the maximum value
of cosine is cos 0 ° = 1 . For this value, dot product simply evaluates to the product of the
magnitudes of two vectors.
For θ = 180 ° , cos 180 ° = - 1 and
Thus, we see that dot product can evaluate to negative value as well. This is a significant result as







many scalar quantities in physics are given negative value. The work done, for example, can be
negative, when displacement is in the opposite direction to the component of force along that
direction.
The scalar product evaluates to zero for θ = 90° and 270° as cosine of these angles are zero. These
results have important implication for unit vectors. The dot products of same unit vector evaluates
to 1.
The dot products of combination of different unit vectors evaluate to zero.
Example 1.8.
Problem : Find the angle between vectors 2 i + j – k and i – k.
Solution : The cosine of the angle between two vectors is given in terms of dot product as :
Now,
Ignoring dot products of different unit vectors (they evaluate to zero), we have :
Putting in the expression of cosine, we have :
Scalar product in component form
Two vectors in component forms are written as :
In evaluating the product, we make use of the fact that multiplication of the same unit vectors is 1,
while multiplication of different unit vectors is zero. The dot product evaluates to scalar terms as :









()
Component as scalar (dot) product
A closer look at the expansion of dot product of two vectors reveals that the expression is very
similar to the expression for a component of a vector. The expression of the dot product is :
On the other hand, the component of a vector in a given direction is :
Comparing two equations, we can define component of a vector in a direction given by unit vector
" n" as :
()
This is a very general and useful relation to determine component of a vector in any direction.
Only requirement is that we should know the unit vector in the direction in which component is to
be determined.
Example 1.9.
Problem : Find the components of vector 2 i + 3 j along the direction i+ j.
Solution : The component of a vector “ a” in a direction, represented by unit vector “ n” is
given by dot product :
Thus, it is clear that we need to find the unit vector in the direction of i+ j. Now, the unit
vector in the direction of the vector is :
Here,
Hence,
The component of vector 2 i + 3 j in the direction of “ n” is :







Attributes of scalar (dot) product
In this section, we summarize the properties of dot product as discussed above. Besides, some
additional derived attributes are included for reference.
1: Dot product is commutative
This means that the dot product of vectors is not dependent on the sequence of vectors :
We must, however, be careful while writing sequence of dot product. For example, writing a
sequence involving three vectors like a.b.c is incorrect. For, dot product of any two vectors is a
scalar. As dot product is defined for two vectors (not one vector and one scalar), the resulting dot
product of a scalar ( a.b) and that of third vector c has no meaning.
2: Distributive property of dot product :
3: The dot product of a vector with itself is equal to the square of the magnitude of the vector.
4: The magnitude of dot product of two vectors can be obtained in either of the following manner :
The dot product of two vectors is equal to the algebraic product of magnitude of one vector and
component of second vector in the direction of first vector.
5: The cosine of the angle between two vectors can be obtained in terms of dot product as :
6: The condition of two perpendicular vectors in terms of dot product is given by :







7: Properties of dot product with respect to unit vectors along the axes of rectangular coordinate
system are :
8: Dot product in component form is :
9: The dot product does not yield to cancellation. For example, if a.b = a.c, then we can not
conclude that b = c. Rearranging, we have :
This means that a and ( b - c) are perpendicular to each other. In turn, this implies that ( b - c) is not equal to zero (null vector). Hence, b is not equal to c as we would get after cancellation.
We can understand this difference with respect to cancellation more explicitly by working through
the problem given here :
Example 1.10.
Problem : Verify vector equality B = C, if A.B = A.C.
Solution : The given equality of dot products is :
We should understand that dot product is not a simple algebraic product of two numbers (read
magnitudes). The angle between two vectors plays a role in determining the magnitude of the
dot product. Hence, it is entirely possible that vectors B and C are different yet their dot
products with common vector A are equal. Let θ 1 and θ 2 be the angles for first and second
pairs of dot products. Then,
If θ 1 = θ 2 , then B = C . However, if θ 1 ≠ θ 2 , then B ≠ C .
Law of cosine and dot product
Law of cosine relates sides of a triangle with one included angle. We can determine this
relationship using property of a dot product. Let three vectors are represented by sides of the
triangle such that closing side is the sum of other two vectors. Then applying triangle law of






addition :
Figure 1.63. Cosine law
Cosine law
We know that the dot product of a vector with itself is equal to the square of the magnitude of the
vector. Hence,
This is known as cosine law of triangle. Curiously, we may pay attention to first two equations
above. As a matter of fact, second equation gives the square of the magnitude of resultant of two
vectors a and b.
Differentiation and dot product
Differentiation of a vector expression yields a vector. Consider a vector expression given as :
The derivative of the vector with respect to x is :
As the derivative is a vector, two vector expressions with dot product is differentiated in a manner
so that dot product is retained in the final expression of derivative. For example,
Exercises
Exercise 15.
Sum and difference of two vectors a and b are perpendicular to each other. Find the relation
between two vectors.