Two techniques have shown considerable promise. The first of these is called magnetic confinement and uses the property that charged particles
have difficulty crossing magnetic field lines. The tokamak, shown in Figure 32.22, has shown particular promise. The tokamak’s toroidal coil confines charged particles into a circular path with a helical twist due to the circulating ions themselves. In 1995, the Tokamak Fusion Test Reactor at
Princeton in the US achieved world-record plasma temperatures as high as 500 million degrees Celsius. This facility operated between 1982 and
1997. A joint international effort is underway in France to build a tokamak-type reactor that will be the stepping stone to commercial power. ITER, as it
is called, will be a full-scale device that aims to demonstrate the feasibility of fusion energy. It will generate 500 MW of power for extended periods of
time and will achieve break-even conditions. It will study plasmas in conditions similar to those expected in a fusion power plant. Completion is
scheduled for 2018.


1164 CHAPTER 32 | MEDICAL APPLICATIONS OF NUCLEAR PHYSICS
Figure 32.22 (a) Artist’s rendition of ITER, a tokamak-type fusion reactor being built in southern France. It is hoped that this gigantic machine will reach the break-even point.
Completion is scheduled for 2018. (credit: Stephan Mosel, Flickr)
The second promising technique aims multiple lasers at tiny fuel pellets filled with a mixture of deuterium and tritium. Huge power input heats the fuel,
evaporating the confining pellet and crushing the fuel to high density with the expanding hot plasma produced. This technique is called inertial
confinement, because the fuel’s inertia prevents it from escaping before significant fusion can take place. Higher densities have been reached than
with tokamaks, but with smaller confinement times. In 2009, the Lawrence Livermore Laboratory (CA) completed a laser fusion device with 192
ultraviolet laser beams that are focused upon a D-T pellet (see Figure 32.23).
Figure 32.23 National Ignition Facility (CA). This image shows a laser bay where 192 laser beams will focus onto a small D-T target, producing fusion. (credit: Lawrence
Livermore National Laboratory, Lawrence Livermore National Security, LLC, and the Department of Energy)
Example 32.2 Calculating Energy and Power from Fusion
(a) Calculate the energy released by the fusion of a 1.00-kg mixture of deuterium and tritium, which produces helium. There are equal numbers
of deuterium and tritium nuclei in the mixture.
(b) If this takes place continuously over a period of a year, what is the average power output?
Strategy
According to 2 H + 3H → 4 He + n , the energy per reaction is 17.59 MeV. To find the total energy released, we must find the number of
deuterium and tritium atoms in a kilogram. Deuterium has an atomic mass of about 2 and tritium has an atomic mass of about 3, for a total of
about 5 g per mole of reactants or about 200 mol in 1.00 kg. To get a more precise figure, we will use the atomic masses from Appendix A. The
power output is best expressed in watts, and so the energy output needs to be calculated in joules and then divided by the number of seconds in
a year.
Solution for (a)
The atomic mass of deuterium ( 2 H ) is 2.014102 u, while that of tritium ( 3 H ) is 3.016049 u, for a total of 5.032151 u per reaction. So a mole of
reactants has a mass of 5.03 g, and in 1.00 kg there are (1000 g) / (5.03 g/mol)=198.8 mol of reactants . The number of reactions that take
place is therefore
(32.23)
(198.8 mol)⎛⎝6.02×1023 mol−1⎞⎠ = 1.20×1026 reactions.
The total energy output is the number of reactions times the energy per reaction:
(32.24)
E = ⎛⎝1.20×1026 reactions⎞⎠(17.59 MeV/reaction)⎛⎝1.602×10−13 J/MeV⎞⎠
= 3.37×1014 J.
Solution for (b)
Power is energy per unit time. One year has 3.16×107 s , so

CHAPTER 32 | MEDICAL APPLICATIONS OF NUCLEAR PHYSICS 1165
(32.25)
P = Et = 3.37×1014 J
3.16×107 s
= 1.07×107 W = 10.7 MW.
Discussion
By now we expect nuclear processes to yield large amounts of energy, and we are not disappointed here. The energy output of 3.37×1014 J
from fusing 1.00 kg of deuterium and tritium is equivalent to 2.6 million gallons of gasoline and about eight times the energy output of the bomb
that destroyed Hiroshima. Yet the average backyard swimming pool has about 6 kg of deuterium in it, so that fuel is plentiful if it can be utilized in
a controlled manner. The average power output over a year is more than 10 MW, impressive but a bit small for a commercial power plant. About
32 times this power output would allow generation of 100 MW of electricity, assuming an efficiency of one-third in converting the fusion energy to
electrical energy.
32.6 Fission
Nuclear fission is a reaction in which a nucleus is split (or fissured). Controlled fission is a reality, whereas controlled fusion is a hope for the future.
Hundreds of nuclear fission power plants around the world attest to the fact that controlled fission is practical and, at least in the short term,
economical, as seen in Figure 32.24. Whereas nuclear power was of little interest for decades following TMI and Chernobyl (and now Fukushima
Daiichi), growing concerns over global warming has brought nuclear power back on the table as a viable energy alternative. By the end of 2009, there
were 442 reactors operating in 30 countries, providing 15% of the world’s electricity. France provides over 75% of its electricity with nuclear power,
while the US has 104 operating reactors providing 20% of its electricity. Australia and New Zealand have none. China is building nuclear power plants
at the rate of one start every month.
Figure 32.24 The people living near this nuclear power plant have no measurable exposure to radiation that is traceable to the plant. About 16% of the world’s electrical power
is generated by controlled nuclear fission in such plants. The cooling towers are the most prominent features but are not unique to nuclear power. The reactor is in the small
domed building to the left of the towers. (credit: Kalmthouts)
Fission is the opposite of fusion and releases energy only when heavy nuclei are split. As noted in Fusion, energy is released if the products of a nuclear reaction have a greater binding energy per nucleon ( BE / A ) than the parent nuclei. Figure 32.25 shows that BE / A is greater for medium-mass nuclei than heavy nuclei, implying that when a heavy nucleus is split, the products have less mass per nucleon, so that mass is destroyed and
energy is released in the reaction. The amount of energy per fission reaction can be large, even by nuclear standards. The graph in Figure 32.25
shows BE / A to be about 7.6 MeV/nucleon for the heaviest nuclei ( A about 240), while BE / A is about 8.6 MeV/nucleon for nuclei having A
about 120. Thus, if a heavy nucleus splits in half, then about 1 MeV per nucleon, or approximately 240 MeV per fission, is released. This is about 10
times the energy per fusion reaction, and about 100 times the energy of the average α , β , or γ decay.
Example 32.3 Calculating Energy Released by Fission
Calculate the energy released in the following spontaneous fission reaction:
238
(32.26)
U → 95 Sr + 140Xe + 3 n
given the atomic masses to be m(238 U) = 238.050784 u , m(95 Sr) = 94.919388 u , m(140 Xe) = 139.921610 u , and
m( n) = 1.008665 u .
Strategy
As always, the energy released is equal to the mass destroyed times c 2 , so we must find the difference in mass between the parent 238 U
and the fission products.
Solution
The products have a total mass of
m
(32.27)
products = 94.919388 u + 139.921610 u + 3(1.008665 u)
= 237.866993 u.
1166 CHAPTER 32 | MEDICAL APPLICATIONS OF NUCLEAR PHYSICS
The mass lost is the mass of 238 U minus m products , or
(32.28)
Δ m = 238.050784 u − 237.8669933 u = 0.183791 u,
so the energy released is
(32.29)
E = (Δ m) c 2
= (0.183791 u)931.5 MeV/ c 2
u
c 2 = 171.2 MeV.
Discussion
A number of important things arise in this example. The 171-MeV energy released is large, but a little less than the earlier estimated 240 MeV.
This is because this fission reaction produces neutrons and does not split the nucleus into two equal parts. Fission of a given nuclide, such as
238 U , does not always produce the same products. Fission is a statistical process in which an entire range of products are produced with
various probabilities. Most fission produces neutrons, although the number varies with each fission. This is an extremely important aspect of
fission, because neutrons can induce more fission, enabling self-sustaining chain reactions.
Spontaneous fission can occur, but this is usually not the most common decay mode for a given nuclide. For example, 238 U can spontaneously
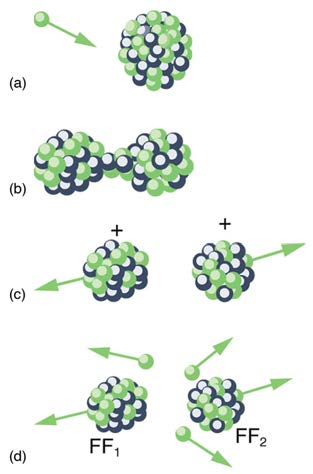
fission, but it decays mostly by α emission. Neutron-induced fission is crucial as seen in Figure 32.25. Being chargeless, even low-energy neutrons can strike a nucleus and be absorbed once they feel the attractive nuclear force. Large nuclei are described by a liquid drop model with surface
tension and oscillation modes, because the large number of nucleons act like atoms in a drop. The neutron is attracted and thus, deposits energy,
causing the nucleus to deform as a liquid drop. If stretched enough, the nucleus narrows in the middle. The number of nucleons in contact and the
strength of the nuclear force binding the nucleus together are reduced. Coulomb repulsion between the two ends then succeeds in fissioning the
nucleus, which pops like a water drop into two large pieces and a few neutrons. Neutron-induced fission can be written as
(32.30)
n + A X → FF1 + FF2 + xn,
where FF1 and FF2 are the two daughter nuclei, called fission fragments, and x is the number of neutrons produced. Most often, the masses of
the fission fragments are not the same. Most of the released energy goes into the kinetic energy of the fission fragments, with the remainder going
into the neutrons and excited states of the fragments. Since neutrons can induce fission, a self-sustaining chain reaction is possible, provided more
than one neutron is produced on average — that is, if x > 1 in n + A X → FF1 + FF2 + xn . This can also be seen in Figure 32.26.
An example of a typical neutron-induced fission reaction is
235
142
91
(32.31)
n + 92 U → 56 Ba + 36Kr + 3 n.
Note that in this equation, the total charge remains the same (is conserved): 92 + 0 = 56 + 36 . Also, as far as whole numbers are concerned, the
mass is constant: 1 + 235 = 142 + 91 + 3 . This is not true when we consider the masses out to 6 or 7 significant places, as in the previous
example.
Figure 32.25 Neutron-induced fission is shown. First, energy is put into this large nucleus when it absorbs a neutron. Acting like a struck liquid drop, the nucleus deforms and begins to narrow in the middle. Since fewer nucleons are in contact, the repulsive Coulomb force is able to break the nucleus into two parts with some neutrons also flying
away.
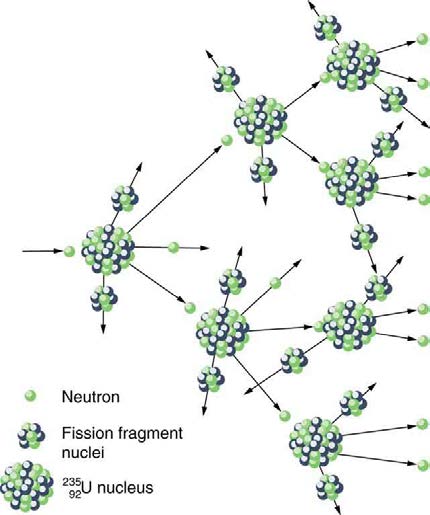
CHAPTER 32 | MEDICAL APPLICATIONS OF NUCLEAR PHYSICS 1167
Figure 32.26 A chain reaction can produce self-sustained fission if each fission produces enough neutrons to induce at least one more fission. This depends on several
factors, including how many neutrons are produced in an average fission and how easy it is to make a particular type of nuclide fission.
Not every neutron produced by fission induces fission. Some neutrons escape the fissionable material, while others interact with a nucleus without
making it fission. We can enhance the number of fissions produced by neutrons by having a large amount of fissionable material. The minimum
amount necessary for self-sustained fission of a given nuclide is called its critical mass. Some nuclides, such as 239 Pu , produce more neutrons
per fission than others, such as 235 U . Additionally, some nuclides are easier to make fission than others. In particular, 235 U and 239 Pu are
easier to fission than the much more abundant 238 U . Both factors affect critical mass, which is smallest for 239 Pu .
The reason 235 U and 239 Pu are easier to fission than 238 U is that the nuclear force is more attractive for an even number of neutrons in a
nucleus than for an odd number. Consider that 235
239
238
92 U143 has 143 neutrons, and 94 P145 has 145 neutrons, whereas 92 U146 has 146. When a
neutron encounters a nucleus with an odd number of neutrons, the nuclear force is more attractive, because the additional neutron will make the
number even. About 2-MeV more energy is deposited in the resulting nucleus than would be the case if the number of neutrons was already even.
This extra energy produces greater deformation, making fission more likely. Thus, 235 U and 239 Pu are superior fission fuels. The isotope 235 U
is only 0.72 % of natural uranium, while 238 U is 99.27%, and 239 Pu does not exist in nature. Australia has the largest deposits of uranium in the
world, standing at 28% of the total. This is followed by Kazakhstan and Canada. The US has only 3% of global reserves.
Most fission reactors utilize 235 U , which is separated from 238 U at some expense. This is called enrichment. The most common separation
method is gaseous diffusion of uranium hexafluoride ( UF6 ) through membranes. Since 235 U has less mass than 238 U , its UF6 molecules
have higher average velocity at the same temperature and diffuse faster. Another interesting characteristic of 235 U is that it preferentially absorbs
very slow moving neutrons (with energies a fraction of an eV), whereas fission reactions produce fast neutrons with energies in the order of an MeV.
To make a self-sustained fission reactor with 235 U , it is thus necessary to slow down (“thermalize”) the neutrons. Water is very effective, since
neutrons collide with protons in water molecules and lose energy. Figure 32.27 shows a schematic of a reactor design, called the pressurized water reactor.
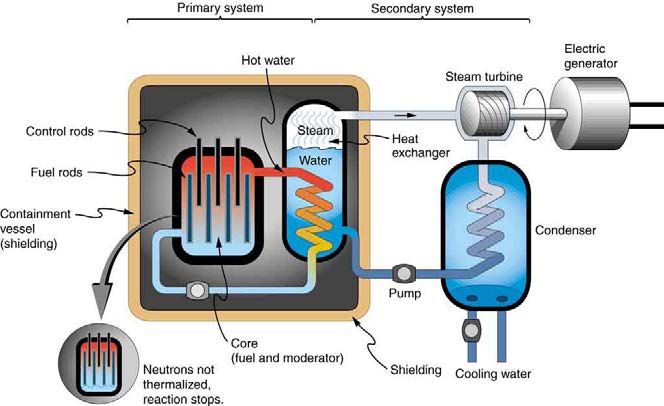
1168 CHAPTER 32 | MEDICAL APPLICATIONS OF NUCLEAR PHYSICS
235
Figure 32.27 A pressurized water reactor is cleverly designed to control the fission of large amounts of
U , while using the heat produced in the fission reaction to create
steam for generating electrical energy. Control rods adjust neutron flux so that criticality is obtained, but not exceeded. In case the reactor overheats and boils the water away,
the chain reaction terminates, because water is needed to thermalize the neutrons. This inherent safety feature can be overwhelmed in extreme circumstances.
Control rods containing nuclides that very strongly absorb neutrons are used to adjust neutron flux. To produce large power, reactors contain
hundreds to thousands of critical masses, and the chain reaction easily becomes self-sustaining, a condition called criticality. Neutron flux should be
carefully regulated to avoid an exponential increase in fissions, a condition called supercriticality. Control rods help prevent overheating, perhaps
even a meltdown or explosive disassembly. The water that is used to thermalize neutrons, necessary to get them to induce fission in 235 U , and
achieve criticality, provides a negative feedback for temperature increases. In case the reactor overheats and boils the water to steam or is breached,
the absence of water kills the chain reaction. Considerable heat, however, can still be generated by the reactor’s radioactive fission products. Other
safety features, thus, need to be incorporated in the event of a loss of coolant accident, including auxiliary cooling water and pumps.
Example 32.4 Calculating Energy from a Kilogram of Fissionable Fuel
Calculate the amount of energy produced by the fission of 1.00 kg of 235 U , given the average fission reaction of 235 U produces 200 MeV.
Strategy
The total energy produced is the number of 235 U atoms times the given energy per 235 U fission. We should therefore find the number of
235 U atoms in 1.00 kg.
Solution
The number of 235 U atoms in 1.00 kg is Avogadro’s number times the number of moles. One mole of 235 U has a mass of 235.04 g; thus,
there are (1000 g) / (235.04 g/mol) = 4.25 mol . The number of 235 U atoms is therefore,
(32.32)
(4.25 mol)⎛⎝6.02×1023 235U/mol⎞⎠ = 2.56×1024 235U.
So the total energy released is
(32.33)
E = ⎛
⎛200 MeV⎞⎛1.60×10−13 J⎞
⎝2.56×1024 235 U⎞⎠⎝ 235 U ⎠⎝ MeV
⎠
= 8.21×1013 J.
Discussion
This is another impressively large amount of energy, equivalent to about 14,000 barrels of crude oil or 600,000 gallons of gasoline. But, it is only
one-fourth the energy produced by the fusion of a kilogram mixture of deuterium and tritium as seen in Example 32.2. Even though each fission
reaction yields about ten times the energy of a fusion reaction, the energy per kilogram of fission fuel is less, because there are far fewer moles
per kilogram of the heavy nuclides. Fission fuel is also much more scarce than fusion fuel, and less than 1% of uranium (the 235 U) is readily
usable.
One nuclide already mentioned is 239 Pu , which has a 24,120-y half-life and does not exist in nature. Plutonium-239 is manufactured from 238 U in
reactors, and it provides an opportunity to utilize the other 99% of natural uranium as an energy source. The following reaction sequence, called
breeding, produces 239 Pu . Breeding begins with neutron capture by 238 U :

CHAPTER 32 | MEDICAL APPLICATIONS OF NUCLEAR PHYSICS 1169
238
(32.34)
U + n → 239 U + γ.
Uranium-239 then β– decays:
(32.35)
239 U → 239Np + β− + ve(t1/2 = 23 min).
Neptunium-239 also β– decays:
(32.36)
239 Np → 239Pu + β− + ve(t1/2 = 2.4 d).
Plutonium-239 builds up in reactor fuel at a rate that depends on the probability of neutron capture by 238 U (all reactor fuel contains more 238 U
than 235 U ). Reactors designed specifically to make plutonium are called breeder reactors. They seem to be inherently more hazardous than
conventional reactors, but it remains unknown whether their hazards can be made economically acceptable. The four reactors at Chernobyl, including
the one that was destroyed, were built to breed plutonium and produce electricity. These reactors had a design that was significantly different from
the pressurized water reactor illustrated above.
Plutonium-239 has advantages over 235 U as a reactor fuel — it produces more neutrons per fission on average, and it is easier for a thermal
neutron to cause it to fission. It is also chemically different from uranium, so it is inherently easier to separate from uranium ore. This means 239 Pu
has a particularly small critical mass, an advantage for nuclear weapons.
PhET Explorations: Nuclear Fission
Start a chain reaction, or introduce non-radioactive isotopes to prevent one. Control energy production in a nuclear reactor!
Figure 32.28 Nuclear Fission (http://cnx.org/content/m42662/1.5/nuclear-fission_en.jar)
32.7 Nuclear Weapons
The world was in turmoil when fission was discovered in 1938. The discovery of fission, made by two German physicists, Otto Hahn and Fritz
Strassman, was quickly verified by two Jewish refugees from Nazi Germany, Lise Meitner and her nephew Otto Frisch. Fermi, among others, soon
found that not only did neutrons induce fission; more neutrons were produced during fission. The possibility of a self-sustained chain reaction was
immediately recognized by leading scientists the world over. The enormous energy known to be in nuclei, but considered inaccessible, now seemed
to be available on a large scale.
Within months after the announcement of the discovery of fission, Adolf Hitler banned the export of uranium from newly occupied Czechoslovakia. It
seemed that the military value of uranium had been recognized in Nazi Germany, and that a serious effort to build a nuclear bomb had begun.
Alarmed scientists, many of them who fled Nazi Germany, decided to take action. None was more famous or revered than Einstein. It was felt that his
help was needed to get the American government to make a serious effort at nuclear weapons as a matter of survival. Leo Szilard, an escaped
Hungarian physicist, took a draft of a letter to Einstein, who, although pacifistic, signed the final version. The letter was for President Franklin
Roosevelt, warning of the German potential to build extremely powerful bombs of a new type. It was sent in August of 1939, just before the German
invasion of Poland that marked the start of World War II.
It was not until December 6, 1941, the day before the Japanese attack on Pearl Harbor, that the United States made a massive commitment to
building a nuclear bomb. The top secret Manhattan Project was a crash program aimed at beating the Germans. It was carried out in remote
locations, such as Los Alamos, New Mexico, whenever possible, and eventually came to cost billions of dollars and employ the efforts of more than
100,000 people. J. Robert Oppenheimer (1904–1967), whose talent and ambitions made him ideal, was chosen to head the project. The first major
step was made by Enrico Fermi and his group in December 1942, when they achieved the first self-sustained nuclear reactor. This first “atomic pile”,
built in a squash court at the University of Chicago, used carbon blocks to thermalize neutrons. It not only proved that the chain reaction was
possible, it began the era of nuclear reactors. Glenn Seaborg, an American chemist and physicist, received the Nobel Prize in physics in 1951 for
discovery of several transuranic elements, including plutonium. Carbon-moderated reactors are relatively inexpensive and simple in design and are
still used for breeding plutonium, such as at Chernobyl, where two such reactors remain in operation.
Plutonium was recognized as easier to fission with neutrons and, hence, a superior fission material very early in the Manhattan Project. Plutonium
availability was uncertain, and so a uranium bomb was developed simultaneously. Figure 32.29 shows a gun-type bomb, which takes two subcritical
uranium masses and blows them together. To get an appreciable yield, the critical mass must be held together by the explosive charges inside the
cannon barrel for a few microseconds. Since the buildup of the uranium chain reaction is relatively slow, the device to hold the critical mass together
can be relatively simple. Owing to the fact that the rate of spontaneous fission is low, a neutron source is triggered at the same time the critical mass
is assembled.
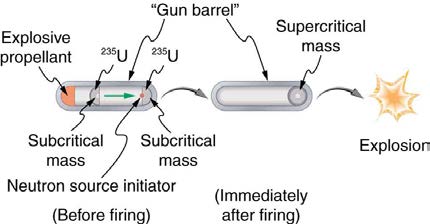

1170 CHAPTER 32 | MEDICAL APPLICATIONS OF NUCLEAR PHYSICS
235
Figure 32.29 A gun-type fission bomb for
U utilizes two subcritical masses forced together by explosive charges inside a cannon barrel. The energy yield depends on
the amount of uranium and the time it can be held together before it disassembles itself.
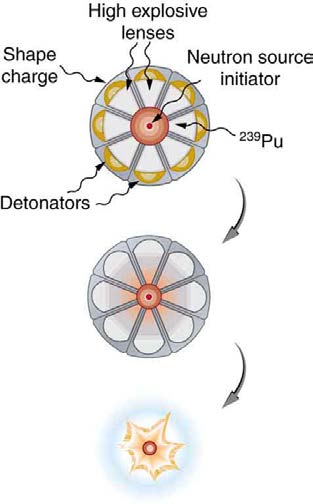
Plutonium’s special properties necessitated a more sophisticated critical mass assembly, shown schematically in













