relative to the target? (b) If the speed of light was this small, would you
10. (a) At what relative velocity is γ = 2.00 ? (b) At what relative velocity observe relativistic effects in everyday life? Discuss.
is γ = 10.0 ?
24. If a galaxy moving away from the Earth has a speed of 1000 km/s
11. Unreasonable Results
and emits 656 nm light characteristic of hydrogen (the most common
element in the universe). (a) What wavelength would we observe on the
(a) Find the value of γ for the following situation. An Earth-bound
Earth? (b) What type of electromagnetic radiation is this? (c) Why is the
observer measures 23.9 h to have passed while signals from a high-
speed of the Earth in its orbit negligible here?
velocity space probe indicate that 24.0 h have passed on board. (b)
25. A space probe speeding towards the nearest star moves at 0.250 c
What is unreasonable about this result? (c) Which assumptions are
and sends radio information at a broadcast frequency of 1.00 GHz. What
unreasonable or inconsistent?
frequency is received on the Earth?
28.3 Length Contraction
26. If two spaceships are heading directly towards each other at 0.800 c
, at what speed must a canister be shot from the first ship to approach
12. A spaceship, 200 m long as seen on board, moves by the Earth at
0.970 c
the other at 0.999 c as seen by the second ship?
. What is its length as measured by an Earth-bound observer?
27. Two planets are on a collision course, heading directly towards each
13. How fast would a 6.0 m-long sports car have to be going past you in
other at 0.250 c . A spaceship sent from one planet approaches the
order for it to appear only 5.5 m long?
second at 0.750 c as seen by the second planet. What is the velocity of
14. (a) How far does the muon in Example 28.1 travel according to the
Earth-bound observer? (b) How far does it travel as viewed by an
the ship relative to the first planet?
observer moving with it? Base your calculation on its velocity relative to
28. When a missile is shot from one spaceship towards another, it leaves
the Earth and the time it lives (proper time). (c) Verify that these two
the first at 0.950 c and approaches the other at 0.750 c . What is the
distances are related through length contraction γ= 3.20 .
relative velocity of the two ships?
15. (a) How long would the muon in Example 28.1 have lived as
29. What is the relative velocity of two spaceships if one fires a missile at
observed on the Earth if its velocity was 0.0500 c ? (b) How far would it
the other at 0.750 c and the other observes it to approach at 0.950 c ?
have traveled as observed on the Earth? (c) What distance is this in the
30. Near the center of our galaxy, hydrogen gas is moving directly away
muon’s frame?
from us in its orbit about a black hole. We receive 1900 nm
16. (a) How long does it take the astronaut in Example 28.2 to travel
electromagnetic radiation and know that it was 1875 nm when emitted by
4.30 ly at 0.99944 c (as measured by the Earth-bound observer)? (b)
the hydrogen gas. What is the speed of the gas?
How long does it take according to the astronaut? (c) Verify that these
31. A highway patrol officer uses a device that measures the speed of
two times are related through time dilation with γ= 30.00 as given.
vehicles by bouncing radar off them and measuring the Doppler shift. The
outgoing radar has a frequency of 100 GHz and the returning echo has a
CHAPTER 28 | SPECIAL RELATIVITY 1029
frequency 15.0 kHz higher. What is the velocity of the vehicle? Note that
47. A supernova explosion of a 2.00×1031 kg star produces
there are two Doppler shifts in echoes. Be certain not to round off until
the end of the problem, because the effect is small.
1.00×1044 kg of energy. (a) How many kilograms of mass are
32. Prove that for any relative velocity v between two observers, a beam converted to energy in the explosion? (b) What is the ratio Δ m / m of
of light sent from one to the other will approach at speed c (provided
mass destroyed to the original mass of the star?
that v is less than c , of course).
48. (a) Using data from Table 7.1, calculate the mass converted to
33. Show that for any relative velocity v between two observers, a beam energy by the fission of 1.00 kg of uranium. (b) What is the ratio of mass
of light projected by one directly away from the other will move away at
destroyed to the original mass, Δ m / m ?
the speed of light (provided that v is less than c , of course).
49. (a) Using data from Table 7.1, calculate the amount of mass
34. (a) All but the closest galaxies are receding from our own Milky Way
converted to energy by the fusion of 1.00 kg of hydrogen. (b) What is the
ratio of mass destroyed to the original mass, Δ m / m ? (c) How does this
Galaxy. If a galaxy 12.0×109 ly ly away is receding from us at 0.
0.900
compare with Δ m / m for the fission of 1.00 kg of uranium?
c , at what velocity relative to us must we send an exploratory
probe to approach the other galaxy at 0.990 c , as measured from that
50. There is approximately 1034 J of energy available from fusion of
galaxy? (b) How long will it take the probe to reach the other galaxy as
hydrogen in the world’s oceans. (a) If 1033 J of this energy were
measured from the Earth? You may assume that the velocity of the other
utilized, what would be the decrease in mass of the oceans? (b) How
galaxy remains constant. (c) How long will it then take for a radio signal
great a volume of water does this correspond to? (c) Comment on
to be beamed back? (All of this is possible in principle, but not practical.)
whether this is a significant fraction of the total mass of the oceans.
28.5 Relativistic Momentum
51. A muon has a rest mass energy of 105.7 MeV, and it decays into an
electron and a massless particle. (a) If all the lost mass is converted into
35. Find the momentum of a helium nucleus having a mass of
the electron’s kinetic energy, find γ for the electron. (b) What is the
6.68×10–27 kg that is moving at 0.200 c .
electron’s velocity?
36. What is the momentum of an electron traveling at 0.980 c ?
52. A π -meson is a particle that decays into a muon and a massless
particle. The π -meson has a rest mass energy of 139.6 MeV, and the
37. (a) Find the momentum of a 1.00×109 kg asteroid heading towards muon has a rest mass energy of 105.7 MeV. Suppose the π -meson is at
the Earth at 30.0 km/s . (b) Find the ratio of this momentum to the
rest and all of the missing mass goes into the muon’s kinetic energy. How
classical momentum. (Hint: Use the approximation that
fast will the muon move?
γ = 1 + (1 / 2) v 2 / c 2 at low velocities.)
53. (a) Calculate the relativistic kinetic energy of a 1000-kg car moving at
30.0 m/s if the speed of light were only 45.0 m/s. (b) Find the ratio of the
38. (a) What is the momentum of a 2000 kg satellite orbiting at 4.00 km/
relativistic kinetic energy to classical.
s? (b) Find the ratio of this momentum to the classical momentum. (Hint:
54. Alpha decay is nuclear decay in which a helium nucleus is emitted. If
Use the approximation that γ = 1 + (1 / 2) v 2 / c 2 at low velocities.)
the helium nucleus has a mass of 6.80×10−27 kg and is given 5.00
39. What is the velocity of an electron that has a momentum of
MeV of kinetic energy, what is its velocity?
3.04×10–21 kg⋅m/s ? Note that you must calculate the velocity to at
55. (a) Beta decay is nuclear decay in which an electron is emitted. If the
least four digits to see the difference from c .
electron is given 0.750 MeV of kinetic energy, what is its velocity? (b)
Comment on how the high velocity is consistent with the kinetic energy
40. Find the velocity of a proton that has a momentum of
as it compares to the rest mass energy of the electron.
4.48×–10-19 kg⋅m/s.
56. A positron is an antimatter version of the electron, having exactly the
same mass. When a positron and an electron meet, they annihilate,
41. (a) Calculate the speed of a 1.00- µ g particle of dust that has the
converting all of their mass into energy. (a) Find the energy released,
same momentum as a proton moving at 0.999 c . (b) What does the
assuming negligible kinetic energy before the annihilation. (b) If this
energy is given to a proton in the form of kinetic energy, what is its
small speed tell us about the mass of a proton compared to even a tiny
velocity? (c) If this energy is given to another electron in the form of
amount of macroscopic matter?
kinetic energy, what is its velocity?
42. (a) Calculate γ for a proton that has a momentum of 1.00 kg⋅m/s.
57. What is the kinetic energy in MeV of a π -meson that lives
(b) What is its speed? Such protons form a rare component of cosmic
1.40×10−16 s as measured in the laboratory, and 0.840×10−16 s
radiation with uncertain origins.
when at rest relative to an observer, given that its rest energy is 135
28.6 Relativistic Energy
MeV?
43. What is the rest energy of an electron, given its mass is
58. Find the kinetic energy in MeV of a neutron with a measured life span
9.11×10−31 kg
of 2065 s, given its rest energy is 939.6 MeV, and rest life span is 900s.
? Give your answer in joules and MeV.
59. (a) Show that ( pc)2 / ( mc 2)2 = γ 2 − 1 . This means that at large
44. Find the rest energy in joules and MeV of a proton, given its mass is
1.67×10−27 kg .
velocities pc>> mc 2 . (b) Is E ≈ pc when γ = 30.0 , as for the
astronaut discussed in the twin paradox?
45. If the rest energies of a proton and a neutron (the two constituents of
nuclei) are 938.3 and 939.6 MeV respectively, what is the difference in
60. One cosmic ray neutron has a velocity of 0.250 c relative to the
their masses in kilograms?
Earth. (a) What is the neutron’s total energy in MeV? (b) Find its
46. The Big Bang that began the universe is estimated to have released
momentum. (c) Is E ≈ pc in this situation? Discuss in terms of the
1068 J of energy. How many stars could half this energy create,
equation given in part (a) of the previous problem.
assuming the average star’s mass is 4.00×1030 kg ?
1030 CHAPTER 28 | SPECIAL RELATIVITY
61. What is γ for a proton having a mass energy of 938.3 MeV
astronaut and ship. Unless your instructor directs you otherwise, do not
accelerated through an effective potential of 1.0 TV (teravolt) at Fermilab
include any energy given to other masses, such as rocket propellants.
outside Chicago?
62. (a) What is the effective accelerating potential for electrons at the
Stanford Linear Accelerator, if γ = 1.00×105 for them? (b) What is
their total energy (nearly the same as kinetic in this case) in GeV?
63. (a) Using data from Table 7.1, find the mass destroyed when the
energy in a barrel of crude oil is released. (b) Given these barrels contain
200 liters and assuming the density of crude oil is 750 kg/m3 , what is
the ratio of mass destroyed to original mass, Δ m / m ?
64. (a) Calculate the energy released by the destruction of 1.00 kg of
mass. (b) How many kilograms could be lifted to a 10.0 km height by this
amount of energy?
65. A Van de Graaff accelerator utilizes a 50.0 MV potential difference to
accelerate charged particles such as protons. (a) What is the velocity of a
proton accelerated by such a potential? (b) An electron?
66. Suppose you use an average of 500 kW·h of electric energy per
month in your home. (a) How long would 1.00 g of mass converted to
electric energy with an efficiency of 38.0% last you? (b) How many
homes could be supplied at the 500 kW·h per month rate for one year
by the energy from the described mass conversion?
67. (a) A nuclear power plant converts energy from nuclear fission into
electricity with an efficiency of 35.0%. How much mass is destroyed in
one year to produce a continuous 1000 MW of electric power? (b) Do you
think it would be possible to observe this mass loss if the total mass of
the fuel is 104 kg ?
68. Nuclear-powered rockets were researched for some years before
safety concerns became paramount. (a) What fraction of a rocket’s mass
would have to be destroyed to get it into a low Earth orbit, neglecting the
decrease in gravity? (Assume an orbital altitude of 250 km, and calculate
both the kinetic energy (classical) and the gravitational potential energy
needed.) (b) If the ship has a mass of 1.00×105 kg (100 tons), what
total yield nuclear explosion in tons of TNT is needed?
69. The Sun produces energy at a rate of 4.00×1026 W by the fusion of
hydrogen. (a) How many kilograms of hydrogen undergo fusion each
second? (b) If the Sun is 90.0% hydrogen and half of this can undergo
fusion before the Sun changes character, how long could it produce
energy at its current rate? (c) How many kilograms of mass is the Sun
losing per second? (d) What fraction of its mass will it have lost in the
time found in part (b)?
70. Unreasonable Results
A proton has a mass of 1.67×10−27 kg . A physicist measures the
proton’s total energy to be 50.0 MeV. (a) What is the proton’s kinetic
energy? (b) What is unreasonable about this result? (c) Which
assumptions are unreasonable or inconsistent?
71. Construct Your Own Problem
Consider a highly relativistic particle. Discuss what is meant by the term
“highly relativistic.” (Note that, in part, it means that the particle cannot be
massless.) Construct a problem in which you calculate the wavelength of
such a particle and show that it is very nearly the same as the
wavelength of a massless particle, such as a photon, with the same
energy. Among the things to be considered are the rest energy of the
particle (it should be a known particle) and its total energy, which should
be large compared to its rest energy.
72. Construct Your Own Problem
Consider an astronaut traveling to another star at a relativistic velocity.
Construct a problem in which you calculate the time for the trip as
observed on the Earth and as observed by the astronaut. Also calculate
the amount of mass that must be converted to energy to get the
astronaut and ship to the velocity travelled. Among the things to be
considered are the distance to the star, the velocity, and the mass of the

CHAPTER 29 | INTRODUCTION TO QUANTUM PHYSICS 1031
29
INTRODUCTION TO QUANTUM PHYSICS
Figure 29.1 A black fly imaged by an electron microscope is as monstrous as any science-fiction creature. (credit: U.S. Department of Agriculture via Wikimedia Commons)
1032 CHAPTER 29 | INTRODUCTION TO QUANTUM PHYSICS
Learning Objectives
29.1. Quantization of Energy
• Explain Max Planck’s contribution to the development of quantum mechanics.
• Define blackbody and blackbody radiation.
• Calculate energy with Planck’s constant.
• Explain why atomic spectra indicate quantization.
29.2. The Photoelectric Effect
• Define what a photon is.
• Describe a typical photoelectric-effect experiment, and explain what experimental observations provide evidence for the photon nature of
light.
• Describe qualitatively how the number of photoelectrons and their maximum kinetic energy depend on the wavelength and intensity of the
light striking the surface, and account for this dependence in terms of a photon model of light.
• Determine the maximum kinetic energy of photoelectrons ejected by photons of one energy or wavelength, when given the maximum
kinetic energy of photoelectrons for a different photon energy or wavelength.
• Sketch or identify a graph of stopping potential versus frequency for a photoelectric-effect experiment; determine from such a graph the
threshold frequency and work function, and calculate an approximate value of h/e.
29.3. Photon Energies and the Electromagnetic Spectrum
• Explain the relationship between the energy of a photon in joules or electron volts and its wavelength or frequency, and consequent
properties.
• Calculate the number of photons per second emitted by a monochromatic source of specific wavelength and power.
29.4. Photon Momentum
• Relate the linear momentum of a photon to its energy or wavelength, and apply linear momentum conservation to simple processes
involving the emission, absorption, or reflection of photons.
• Describe Compton’s experiment, and state what results were observed and by what sort of analysis these results may be explained.
• Account qualitatively for the increase of photon wavelength that is observed, and explain the significance of the Compton wavelength.
29.5. The Particle-Wave Duality
• Explain what the term particle-wave duality means, and why it is applied to EM radiation.
29.6. The Wave Nature of Matter
• Calculate the wavelength of a particle as a function of its momentum.
• Describe the Davisson-Germer experiment, and explain how it provides evidence for the wave nature of electrons.
29.7. Probability: The Heisenberg Uncertainty Principle
• Define what a probability distribution is, and explain why we use them.
• Use both versions of Heisenberg’s uncertainty principle in calculations.
• Explain the implications of Heisenberg’s uncertainty principle for measurements.
29.8. The Particle-Wave Duality Reviewed
• Explain the concept of particle-wave duality, and its scope.
Introduction to Quantum Physics
Quantum mechanics is the branch of physics needed to deal with submicroscopic objects. Because these objects are smaller than we can observe
directly with our senses and generally must be observed with the aid of instruments, parts of quantum mechanics seem as foreign and bizarre as
parts of relativity. But, like relativity, quantum mechanics has been shown to be valid—truth is often stranger than fiction.
Certain aspects of quantum mechanics are familiar to us. We accept as fact that matter is composed of atoms, the smallest unit of an element, and
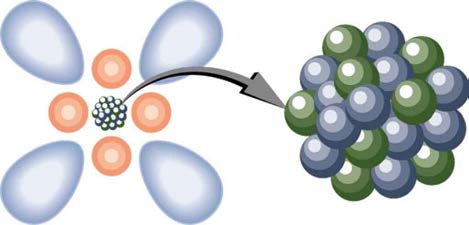
that these atoms combine to form molecules, the smallest unit of a compound. (See Figure 29.2.) While we cannot see the individual water
molecules in a stream, for example, we are aware that this is because molecules are so small and so numerous in that stream. When introducing
atoms, we commonly say that electrons orbit atoms in discrete shells around a tiny nucleus, itself composed of smaller particles called protons and
neutrons. We are also aware that electric charge comes in tiny units carried almost entirely by electrons and protons. As with water molecules in a
stream, we do not notice individual charges in the current through a lightbulb, because the charges are so small and so numerous in the macroscopic
situations we sense directly.
Figure 29.2 Atoms and their substructure are familiar examples of objects that require quantum mechanics to be fully explained. Certain of their characteristics, such as the
discrete electron shells, are classical physics explanations. In quantum mechanics we conceptualize discrete “electron clouds” around the nucleus.
Making Connections: Realms of Physics
Classical physics is a good approximation of modern physics under conditions first discussed in the The Nature of Science and Physics.
Quantum mechanics is valid in general, and it must be used rather than classical physics to describe small objects, such as atoms.
Atoms, molecules, and fundamental electron and proton charges are all examples of physical entities that are quantized—that is, they appear only in
certain discrete values and do not have every conceivable value. Quantized is the opposite of continuous. We cannot have a fraction of an atom, or
CHAPTER 29 | INTRODUCTION TO QUANTUM PHYSICS 1033
part of an electron’s charge, or 14-1/3 cents, for example. Rather, everything is built of integral multiples of these substructures. Quantum physics is
the branch of physics that deals with small objects and the quantization of various entities, including energy and angular momentum. Just as with
classical physics, quantum physics has several subfields, such as mechanics and the study of electromagnetic forces. The correspondence
principle states that in the classical limit (large, slow-moving objects), quantum mechanics becomes the same as classical physics. In this chapter,
we begin the development of quantum mechanics and its description of the strange submicroscopic world. In later chapters, we will examine many
areas, such as atomic and nuclear physics, in which quantum mechanics is crucial.
29.1 Quantization of Energy
Planck’s Contribution
Energy is quantized in some systems, meaning that the system can have only certain energies and not a continuum of energies, unlike the classical
case. This would be like having only certain speeds at which a car can travel because its kinetic energy can have only certain values. We also find
that some forms of energy transfer take place with discrete lumps of energy. While most of us are familiar with the quantization of matter into lumps
called atoms, molecules, and the like






