= 2.88×10−10 kg
20.0 kg
×100%
= 1.44×10−9 %.
Discussion
Both the actual increase in mass and the percent increase are very small, since energy is divided by c 2 , a very large number. We would have to
be able to measure the mass of the battery to a precision of a billionth of a percent, or 1 part in 1011 , to notice this increase. It is no wonder that
the mass variation is not readily observed. In fact, this change in mass is so small that we may question how you could verify it is real. The
answer is found in nuclear processes in which the percentage of mass destroyed is large enough to be measured. The mass of the fuel of a
nuclear reactor, for example, is measurably smaller when its energy has been used. In that case, stored energy has been released (converted
mostly to heat and electricity) and the rest mass has decreased. This is also the case when you use the energy stored in a battery, except that
the stored energy is much greater in nuclear processes, making the change in mass measurable in practice as well as in theory.
Kinetic Energy and the Ultimate Speed Limit
Kinetic energy is energy of motion. Classically, kinetic energy has the familiar expression 1
2 mv 2 . The relativistic expression for kinetic energy is
obtained from the work-energy theorem. This theorem states that the net work on a system goes into kinetic energy. If our system starts from rest,
then the work-energy theorem is
W
(28.50)
net = KE.
Relativistically, at rest we have rest energy E 0 = mc 2 . The work increases this to the total energy E = γmc 2 . Thus,
(28.51)
W net = E − E 0 = γmc 2 − mc 2 = ⎛⎝ γ − 1⎞⎠ mc 2.
Relativistically, we have W net = KErel .
Relativistic Kinetic Energy
Relativistic kinetic energy is
(28.52)
KErel = ⎛⎝ γ − 1⎞⎠ mc 2.
When motionless, we have v = 0 and
CHAPTER 28 | SPECIAL RELATIVITY 1021
(28.53)
γ =
1
= 1,
1 − v 2
c 2
so that KErel = 0 at rest, as expected. But the expression for relativistic kinetic energy (such as total energy and rest energy) does not look much
like the classical 1
2 mv 2 . To show that the classical expression for kinetic energy is obtained at low velocities, we note that the binomial expansion for
γ at low velocities gives
(28.54)
γ = 1 + 1 v 2
2 c 2.
A binomial expansion is a way of expressing an algebraic quantity as a sum of an infinite series of terms. In some cases, as in the limit of small
velocity here, most terms are very small. Thus the expression derived for γ here is not exact, but it is a very accurate approximation. Thus, at low
velocities,
(28.55)
γ − 1 = 1 v 2
2 c 2.
Entering this into the expression for relativistic kinetic energy gives
(28.56)
KE
v 2⎤
rel = ⎡⎣12 c 2⎦ mc 2 = 12 mv 2 = KEclass.
So, in fact, relativistic kinetic energy does become the same as classical kinetic energy when v<< c .
It is even more interesting to investigate what happens to kinetic energy when the velocity of an object approaches the speed of light. We know that
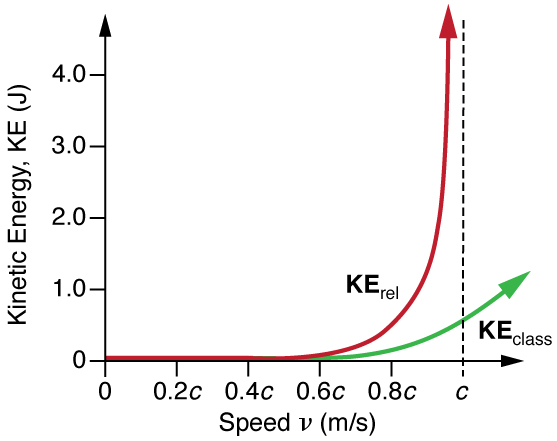
γ becomes infinite as v approaches c , so that KErel also becomes infinite as the velocity approaches the speed of light. (See Figure 28.22.) An
infinite amount of work (and, hence, an infinite amount of energy input) is required to accelerate a mass to the speed of light.
The Speed of Light
No object with mass can attain the speed of light.
So the speed of light is the ultimate speed limit for any particle having mass. All of this is consistent with the fact that velocities less than c always
add to less than c . Both the relativistic form for kinetic energy and the ultimate speed limit being c have been confirmed in detail in numerous
experiments. No matter how much energy is put into accelerating a mass, its velocity can only approach—not reach—the speed of light.
Figure 28.22 This graph of KErel versus velocity shows how kinetic energy approaches infinity as velocity approaches the speed of light. It is thus not possible for an object
having mass to reach the speed of light. Also shown is KEclass , the classical kinetic energy, which is similar to relativistic kinetic energy at low velocities. Note that much
more energy is required to reach high velocities than predicted classically.
Example 28.8 Comparing Kinetic Energy: Relativistic Energy Versus Classical Kinetic Energy
An electron has a velocity v = 0.990 c . (a) Calculate the kinetic energy in MeV of the electron. (b) Compare this with the classical value for
kinetic energy at this velocity. (The mass of an electron is 9.11×10−31 kg .)
Strategy
The expression for relativistic kinetic energy is always correct, but for (a) it must be used since the velocity is highly relativistic (close to c ). First,
we will calculate the relativistic factor γ , and then use it to determine the relativistic kinetic energy. For (b), we will calculate the classical kinetic
energy (which would be close to the relativistic value if v were less than a few percent of c ) and see that it is not the same.
1022 CHAPTER 28 | SPECIAL RELATIVITY
Solution for (a)
1. Identify the knowns. v = 0.990 c ; m = 9.11×10−31 kg
2. Identify the unknown. KErel
3. Choose the appropriate equation. KErel = ⎛⎝ γ − 1⎞⎠ mc 2
4. Plug the knowns into the equation.
First calculate γ . We will carry extra digits because this is an intermediate calculation.
(28.57)
γ =
1
1 − v 2
c 2
=
1
1 − (0.990 c)2
c 2
=
1
1 − (0.990)2
= 7.0888
Next, we use this value to calculate the kinetic energy.
(28.58)
KErel = ( γ − 1) mc 2
= (7.0888 − 1)(9.11×10 – 31 kg)(3.00×108 m/s)2
= 4.99×10–13 J
5. Convert units.
(28.59)
KE
1 MeV
⎞
rel = (4.99×10–13 J)⎛⎝1.60×10 – 13 J⎠
= 3.12 MeV
Solution for (b)
1. List the knowns. v = 0.990 c ; m = 9.11×10−31 kg
2. List the unknown. KEclass
3. Choose the appropriate equation. KEclass = 12 mv 2
4. Plug the knowns into the equation.
(28.60)
KEclass = 12 mv 2
= 12(9.00×10 – 31 kg)(0.990)2(3.00×108 m/s)2
= 4.02×10 – 14 J
5. Convert units.
(28.61)
KE
1 MeV
⎞
class = 4.02×10 – 14 J⎛⎝1.60×10 – 13 J⎠
= 0.251 MeV
Discussion
As might be expected, since the velocity is 99.0% of the speed of light, the classical kinetic energy is significantly off from the correct relativistic
value. Note also that the classical value is much smaller than the relativistic value. In fact, KErel /KEclass = 12.4 here. This is some indication
of how difficult it is to get a mass moving close to the speed of light. Much more energy is required than predicted classically. Some people
interpret this extra energy as going into increasing the mass of the system, but, as discussed in Relativistic Momentum, this cannot be verified
unambiguously. What is certain is that ever-increasing amounts of energy are needed to get the velocity of a mass a little closer to that of light.
An energy of 3 MeV is a very small amount for an electron, and it can be achieved with present-day particle accelerators. SLAC, for example,
can accelerate electrons to over 50×109 eV = 50,000 MeV .
Is there any point in getting v a little closer to c than 99.0% or 99.9%? The answer is yes. We learn a great deal by doing this. The energy that
goes into a high-velocity mass can be converted to any other form, including into entirely new masses. (See Figure 28.23.) Most of what we
know about the substructure of matter and the collection of exotic short-lived particles in nature has been learned this way. Particles are
accelerated to extremely relativistic energies and made to collide with other particles, producing totally new species of particles. Patterns in the
characteristics of these previously unknown particles hint at a basic substructure for all matter. These particles and some of their characteristics
will be covered in Particle Physics.

CHAPTER 28 | SPECIAL RELATIVITY 1023
Figure 28.23 The Fermi National Accelerator Laboratory, near Batavia, Illinois, was a subatomic particle collider that accelerated protons and antiprotons to attain
energies up to 1 Tev (a trillion electronvolts). The circular ponds near the rings were built to dissipate waste heat. This accelerator was shut down in September 2011.
(credit: Fermilab, Reidar Hahn)
Relativistic Energy and Momentum
We know classically that kinetic energy and momentum are related to each other, since
(28.62)
KEclass = p 2
2 m = ( mv)2
2 m = 12 mv 2.
Relativistically, we can obtain a relationship between energy and momentum by algebraically manipulating their definitions. This produces
(28.63)
E 2 = ( pc)2 + ( mc 2)2,
where E is the relativistic total energy and p is the relativistic momentum. This relationship between relativistic energy and relativistic momentum is
more complicated than the classical, but we can gain some interesting new insights by examining it. First, total energy is related to momentum and
rest mass. At rest, momentum is zero, and the equation gives the total energy to be the rest energy mc 2 (so this equation is consistent with the
discussion of rest energy above). However, as the mass is accelerated, its momentum p increases, thus increasing the total energy. At sufficiently
high velocities, the rest energy term ( mc 2)2 becomes negligible compared with the momentum term ( pc)2 ; thus, E = pc at extremely relativistic
velocities.
If we consider momentum p to be distinct from mass, we can determine the implications of the equation E 2 = ( pc)2 + ( mc 2)2, for a particle that
has no mass. If we take m to be zero in this equation, then E = pc , or p = E / c . Massless particles have this momentum. There are several massless particles found in nature, including photons (these are quanta of electromagnetic radiation). Another implication is that a massless particle
must travel at speed c and only at speed c . While it is beyond the scope of this text to examine the relationship in the equation
E 2 = ( pc)2 + ( mc 2)2, in detail, we can see that the relationship has important implications in special relativity.
Problem-Solving Strategies for Relativity
1. Examine the situation to determine that it is necessary to use relativity. Relativistic effects are related to γ =
1
, the quantitative
1 − v 2
c 2
relativistic factor. If γ is very close to 1, then relativistic effects are small and differ very little from the usually easier classical calculations.
2. Identify exactly what needs to be determined in the problem (identify the unknowns).
3. Make a list of what is given or can be inferred from the problem as stated (identify the knowns). Look in particular for information on relative
velocity v .
4. Make certain you understand the conceptual aspects of the problem before making any calculations. Decide, for example, which observer
sees time dilated or length contracted before plugging into equations. If you have thought about who sees what, who is moving with the
event being observed, who sees proper time, and so on, you will find it much easier to determine if your calculation is reasonable.
5. Determine the primary type of calculation to be done to find the unknowns identified above. You will find the section summary helpful in
determining whether a length contraction, relativistic kinetic energy, or some other concept is involved.
6. Do not round off during the calculation. As noted in the text, you must often perform your calculations to many digits to see the desired
effect. You may round off at the very end of the problem, but do not use a rounded number in a subsequent calculation.
7. Check the answer to see if it is reasonable: Does it make sense? This may be more difficult for relativity, since we do not encounter it
directly. But you can look for velocities greater than c or relativistic effects that are in the wrong direction (such as a time contraction where
a dilation was expected).
Check Your Understanding
A photon decays into an electron-positron pair. What is the kinetic energy of the electron if its speed is 0.992 c ?
Solution
1024 CHAPTER 28 | SPECIAL RELATIVITY
⎛
⎞
(28.64)
⎜
⎟
KE
1
rel = ( γ − 1) mc 2 = ⎜
− 1⎟ mc 2
⎜
⎟
⎝ 1 − v 2
c 2
⎠
⎛
⎞
⎜
⎟
= ⎜
1
− 1⎟(9.11×10−31 kg)(3.00×108 m/s)2 = 5.67×10−13 J
⎜
⎟
⎝ 1 − (0.992 c)2
c 2
⎠
Glossary
classical velocity addition: the method of adding velocities when v<< c ; velocities add like regular numbers in one-dimensional motion:
u = v+u′ , where v is the velocity between two observers, u is the velocity of an object relative to one observer, and u′ is the velocity
relative to the other observer
first postulate of special relativity: the idea that the laws of physics are the same and can be stated in their simplest form in all inertial frames of
reference
inertial frame of reference: a reference frame in which a body at rest remains at rest and a body in motion moves at a constant speed in a
straight line unless acted on by an outside force
length contraction: L , the shortening of the measured length of an object moving relative to the observer’s frame: L=L 0 1− v 2 c 2 = L 0 γ
Michelson-Morley experiment: an investigation performed in 1887 that proved that the speed of light in a vacuum is the same in all frames of
reference from which it is viewed
proper length: L 0 ; the distance between two points measured by an observer who is at rest relative to both of the points; Earth-bound observers
measure proper length when measuring the distance between two points that are stationary relative to the Earth
proper time: Δ t 0. the time measured by an observer at rest relative to the event being observed: Δ t = Δ t 0 = γΔ t 0, where γ = 1
1 − v 2
1 − v 2
c 2
c 2
relativistic Doppler effects: a change in wavelength of radiation that is moving relative to the observer; the wavelength of the radiation is longer
(called a red shift) than that emitted by the source when the source moves away from the observer and shorter (called a blue shift) when the
source moves toward the observer; the shifted wavelength is described by the equation
λ
1 + uc
obs =λs 1 − uc
where λ obs is the observed wavelength, λs is the source wavelength, and u is the velocity of the source to the observer
relativistic kinetic energy: the kinetic energy of an object moving at relativistic speeds: KErel = ⎛⎝ γ − 1⎞⎠ mc 2 , where γ = 1
1 − v 2
c 2
relativistic momentum: p , the momentum of an object moving at relativistic velocity; p = γmu , where m is the rest mass of the object, u is its velocity relative to an observer, and the relativistic factor γ =
1
1 − u 2
c 2
relativistic velocity addition: the method of adding velocities of an object moving at a relativistic speed: u= v+u′ , where v is the relative
1 + vu′
c 2
velocity between two observers, u is the velocity of an object relative to one observer, and u′ is the velocity relative to the other observer
relativity: the study of how different observers measure the same event
rest energy: the energy stored in an object at rest: E 0 = mc 2
rest mass: the mass of an object as measured by a person at rest relative to the object
second postulate of special relativity: the idea that the speed of light c is a constant, independent of the relative motion of the source and
observer
CHAPTER 28 | SPECIAL RELATIVITY 1025
special relativity: the theory that, in an inertial frame of reference, the motion of an object is relative to the frame from which it is viewed or
measured
time dilation: the phenomenon of time passing slower to an observer who is moving relative to another observer
total energy: defined as E = γmc 2 , where γ =
1
1 − v 2
c 2
twin paradox: this asks why a twin traveling at a relativistic speed away and then back towards the Earth ages less than the Earth-bound twin.
The premise to the paradox is faulty because the traveling twin is accelerating, and special relativity does not apply to accelerating frames of
reference
Section Summary
28.1 Einstein’s Postulates
• Relativity is the study of how different observers measure the same event.
• Modern relativity is divided into two parts. Special relativity deals with observers who are in uniform (unaccelerated) motion, whereas general
relativity includes accelerated relative motion and gravity. Modern relativity is correct in all circumstances and, in the limit of low velocity and
weak gravitation, gives the same predictions as classical relativity.
• An inertial frame of reference is a reference frame in which a body at rest remains at rest and a body in motion moves at a constant speed in a
straight line unless acted on by an outside force.
• Modern relativity is based on Einstein’s two postulates. The first postulate of special relativity is the idea that the laws of physics are the same
and can be stated in their simplest form in all inertial frames of reference. The second postulate of special relativity is the idea that the speed of
light c is a constant, independent of the relative motion of the source and observer.
• The Michelson-Morley experiment demonstrated that the speed of light in a vacuum is independent of the motion of the Earth about the Sun.
28.2 Simultaneity And Time Dilation
• Two events are defined to be simultaneous if an observer measures them as occurring at the same time. They are not necessarily simultaneous
to all observers—simultaneity is not absolute.
• Time dilation is the phenomenon of time passing slower for an observer who is moving relative to another observer.
• Observers moving at a relative velocity v do not measure the same elapsed time for an event. Proper time Δ t 0 is the time measured by an
observer at rest relative to the event being observed. Proper time is related to the time Δ t measured by an Earth-bound observer by the
equation
Δ t = Δ t 0 = γΔ t 0,
1 − v 2
c 2
where
γ =
1 .
1 − v 2
c 2
• The equation relating proper time and time measured by an Earth-bound observer implies that relative velocity cannot exceed the speed of light.
• The twin paradox asks why a twin traveling at a relativistic speed away and then back towards the Earth ages less than the Earth-bound twin.
The premise to the paradox is faulty because the traveling twin is accelerating. Special relativity does not apply to accelerating frames of
reference.
• Time dilation is usually negligible at low relative velocities, but it does occur, and it has been verified by experiment.
28.3 Length Contraction
• All observers agree upon relative speed.
• Distance depends on an observer’s motion. Proper length L 0 is the distance between two points measured by an observer who is at rest
relative to both of the points. Earth-bound observers measure proper length when measuring the distance between two points that are
stationary relative to the Earth.
• Length contraction L is the shortening of the measured length of an object moving relative to the observer’s frame:
L=L 0 1 − v 2
c 2 = L 0
γ .
28.4 Relativistic Addition of Velocities
• With class





