Equilibrium
Point charges located at 1.00, 5.00, 8.00, and 14.0 cm along the x-axis.
42. (a) Find the total electric field at x = 1.00 cm in Figure 18.52(b)
37. Sketch the electric field lines in the vicinity of the conductor in Figure
18.48 given the field was originally uniform and parallel to the object’s
given that q = 5.00 nC . (b) Find the total electric field at
long axis. Is the resulting field small near the long side of the object?
x = 11.00 cm in Figure 18.52(b). (c) If the charges are allowed to
move and eventually be brought to rest by friction, what will the final
charge configuration be? (That is, will there be a single charge, double
charge, etc., and what will its value(s) be?)
43. (a) Find the electric field at x = 5.00 cm in Figure 18.52(a), given
that q = 1.00 μC . (b) At what position between 3.00 and 8.00 cm is the
Figure 18.48
total electric field the same as that for –2 q alone? (c) Can the electric
38. Sketch the electric field lines in the vicinity of the conductor in Figure
18.49 given the field was originally uniform and parallel to the object’s
field be zero anywhere between 0.00 and 8.00 cm? (d) At very large
long axis. Is the resulting field small near the long side of the object?
positive or negative values of x, the electric field approaches zero in both
(a) and (b). In which does it most rapidly approach zero and why? (e) At
what position to the right of 11.0 cm is the total electric field zero, other
than at infinity? (Hint: A graphing calculator can yield considerable insight
in this problem.)
44. (a) Find the total Coulomb force on a charge of 2.00 nC located at
x = 4.00 cm in Figure 18.52 (b), given that q = 1.00 μC . (b) Find the
x-position at which the electric field is zero in Figure 18.52 (b).
Figure 18.49
39. Sketch the electric field between the two conducting plates shown in
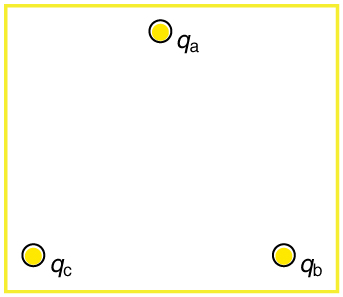
45. Using the symmetry of the arrangement, determine the direction of
Figure 18.50, given the top plate is positive and an equal amount of
the force on q in the figure below, given that qa = qb=+7.50 μC and
negative charge is on the bottom plate. Be certain to indicate the
qc = q
distribution of charge on the plates.
d = −7.50 μC . (b) Calculate the magnitude of the force on the
charge q , given that the square is 10.0 cm on a side and q = 2.00 μC .
Figure 18.50
CHAPTER 18 | ELECTRIC CHARGE AND ELECTRIC FIELD 659
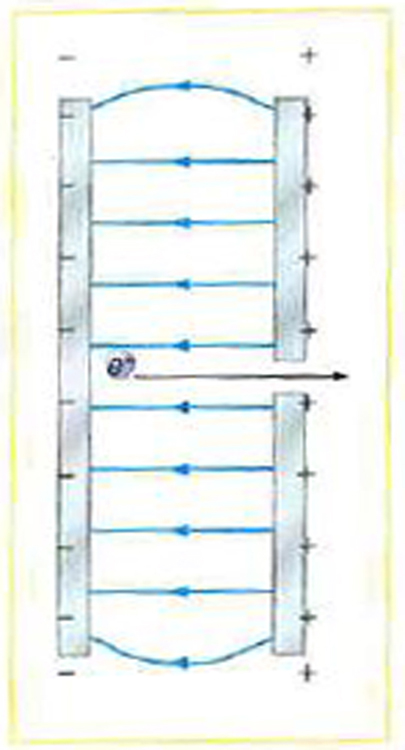
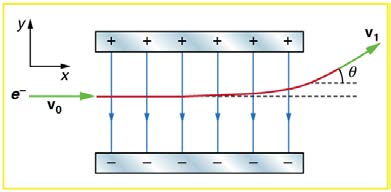
53. A simple and common technique for accelerating electrons is shown
in Figure 18.55, where there is a uniform electric field between two
plates. Electrons are released, usually from a hot filament, near the
negative plate, and there is a small hole in the positive plate that allows
the electrons to continue moving. (a) Calculate the acceleration of the
electron if the field strength is 2.50×104 N/C . (b) Explain why the
electron will not be pulled back to the positive plate once it moves
through the hole.
Figure 18.53
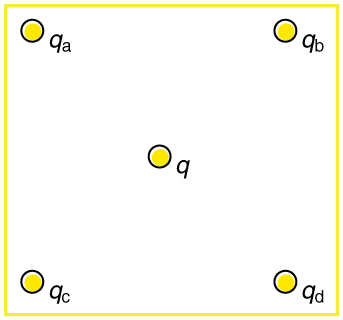
46. (a) Using the symmetry of the arrangement, determine the direction
of the electric field at the center of the square in Figure 18.53, given that
qa = qb = −1.00 μC and qc = qd=+1.00 μC . (b) Calculate the
magnitude of the electric field at the location of q , given that the square
is 5.00 cm on a side.
47. Find the electric field at the location of qa in Figure 18.53 given that
qb = qc = qd=+2.00 nC , q = −1.00 nC , and the square is 20.0 cm
on a side.
48. Find the total Coulomb force on the charge q in Figure 18.53, given
that q = 1.00 μC , qa = 2.00 μC , qb = −3.00 μC ,
qc = −4.00 μC , and qd =+1.00 μC . The square is 50.0 cm on a
side.
49. (a) Find the electric field at the location of qa in Figure 18.54, given
that q b = +10.00 µ C and q c = –5.00 µ C . (b) What is the force on
qa , given that q a = +1.50 nC ?
Figure 18.55 Parallel conducting plates with opposite charges on them create a
relatively uniform electric field used to accelerate electrons to the right. Those that go
through the hole can be used to make a TV or computer screen glow or to produce X-
rays.
54. Earth has a net charge that produces an electric field of
approximately 150 N/C downward at its surface. (a) What is the
magnitude and sign of the excess charge, noting the electric field of a
conducting sphere is equivalent to a point charge at its center? (b) What
acceleration will the field produce on a free electron near Earth’s
surface? (c) What mass object with a single extra electron will have its
weight supported by this field?
55. Point charges of 25.0 µ C and 45.0 µ C are placed 0.500 m apart.
(a) At what point along the line between them is the electric field zero?
Figure 18.54 Point charges located at the corners of an equilateral triangle 25.0 cm
(b) What is the electric field halfway between them?
on a side.
56. What can you say about two charges q
50. (a) Find the electric field at the center of the triangular configuration of
1 and q 2 , if the electric field
charges in Figure 18.54, given that qa =+2.50 nC , qb = −8.00 nC , one-fourth of the way from q 1 to q 2 is zero?
and qc =+1.50 nC . (b) Is there any combination of charges, other than 57. Integrated Concepts
qa = qb = qc , that will produce a zero strength electric field at the
Calculate the angular velocity ω of an electron orbiting a proton in the
center of the triangular configuration?
hydrogen atom, given the radius of the orbit is 0.530×10–10 m . You
18.8 Applications of Electrostatics
may assume that the proton is stationary and the centripetal force is
supplied by Coulomb attraction.
51. (a) What is the electric field 5.00 m from the center of the terminal of
58. Integrated Concepts
a Van de Graaff with a 3.00 mC charge, noting that the field is equivalent
to that of a point charge at the center of the terminal? (b) At this distance,
An electron has an initial velocity of 5.00×106 m/s in a uniform
what force does the field exert on a 2.00 µ C charge on the Van de
2.00×105 N/C strength electric field. The field accelerates the electron
Graaff’s belt?
in the direction opposite to its initial velocity. (a) What is the direction of
52. (a) What is the direction and magnitude of an electric field that
the electric field? (b) How far does the electron travel before coming to
supports the weight of a free electron near the surface of Earth? (b)
rest? (c) How long does it take the electron to come to rest? (d) What is
Discuss what the small value for this field implies regarding the relative
the electron’s velocity when it returns to its starting point?
strength of the gravitational and electrostatic forces.
59. Integrated Concepts
660 CHAPTER 18 | ELECTRIC CHARGE AND ELECTRIC FIELD
The practical limit to an electric field in air is about 3.00×106 N/C .
Above this strength, sparking takes place because air begins to ionize
and charges flow, reducing the field. (a) Calculate the distance a free
proton must travel in this field to reach 3.00% of the speed of light,
starting from rest. (b) Is this practical in air, or must it occur in a vacuum?
60. Integrated Concepts
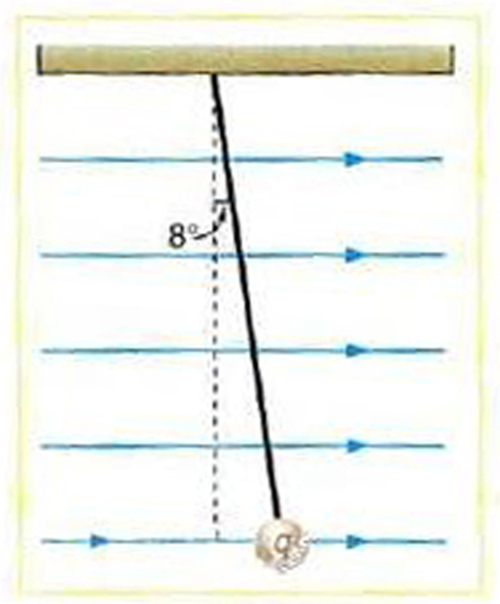
A 5.00 g charged insulating ball hangs on a 30.0 cm long string in a
uniform horizontal electric field as shown in Figure 18.56. Given the
charge on the ball is 1.00 µ C , find the strength of the field.
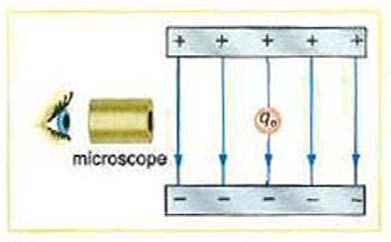
Figure 18.58 In the Millikan oil drop experiment, small drops can be suspended in an
electric field by the force exerted on a single excess electron. Classically, this
experiment was used to determine the electron charge q e by measuring the electric
field and mass of the drop.
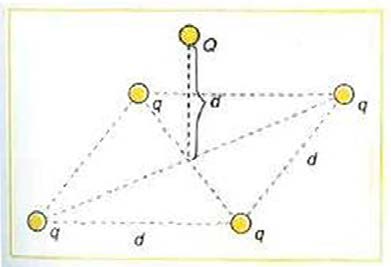
63. Integrated Concepts
(a) In Figure 18.59, four equal charges q lie on the corners of a square.
A fifth charge Q is on a mass m directly above the center of the
square, at a height equal to the length d of one side of the square.
Determine the magnitude of q in terms of Q , m , and d , if the
Coulomb force is to equal the weight of m . (b) Is this equilibrium stable
or unstable? Discuss.
Figure 18.56 A horizontal electric field causes the charged ball to hang at an angle of
8.00º .
61. Integrated Concepts
Figure 18.57 shows an electron passing between two charged metal
plates that create an 100 N/C vertical electric field perpendicular to the
Figure 18.59 Four equal charges on the corners of a horizontal square support the
electron’s original horizontal velocity. (These can be used to change the
weight of a fifth charge located directly above the center of the square.
electron’s direction, such as in an oscilloscope.) The initial speed of the
64. Unreasonable Results
electron is 3.00×106 m/s , and the horizontal distance it travels in the
(a) Calculate the electric field strength near a 10.0 cm diameter
uniform field is 4.00 cm. (a) What is its vertical deflection? (b) What is the
conducting sphere that has 1.00 C of excess charge on it. (b) What is
vertical component of its final velocity? (c) At what angle does it exit?
unreasonable about this result? (c) Which assumptions are responsible?
Neglect any edge effects.
65. Unreasonable Results
(a) Two 0.500 g raindrops in a thunderhead are 1.00 cm apart when they
each acquire 1.00 mC charges. Find their acceleration. (b) What is
unreasonable about this result? (c) Which premise or assumption is
responsible?
66. Unreasonable Results
A wrecking yard inventor wants to pick up cars by charging a 0.400 m
diameter ball and inducing an equal and opposite charge on the car. If a
car has a 1000 kg mass and the ball is to be able to lift it from a distance
of 1.00 m: (a) What minimum charge must be used? (b) What is the
Figure 18.57
electric field near the surface of the ball? (c) Why are these results
62. Integrated Concepts
unreasonable? (d) Which premise or assumption is responsible?
The classic Millikan oil drop experiment was the first to obtain an
67. Construct Your Own Problem
accurate measurement of the charge on an electron. In it, oil drops were
suspended against the gravitational force by a vertical electric field. (See
Consider two insulating balls with evenly distributed equal and opposite
charges on their surfaces, held with a certain distance between the
Figure 18.58.) Given the oil drop to be 1.00 µ m in radius and have a
centers of the balls. Construct a problem in which you calculate the
density of 920 kg/m3 : (a) Find the weight of the drop. (b) If the drop
electric field (magnitude and direction) due to the balls at various points
along a line running through the centers of the balls and extending to
has a single excess electron, find the electric field strength needed to
infinity on either side. Choose interesting points and comment on the
balance its weight.
meaning of the field at those points. For example, at what points might
the field be just that due to one ball and where does the field become
negligibly small? Among the things to be considered are the magnitudes
of the charges and the distance between the centers of the balls. Your
CHAPTER 18 | ELECTRIC CHARGE AND ELECTRIC FIELD 661
instructor may wish for you to consider the electric field off axis or for a
more complex array of charges, such as those in a water molecule.
68. Construct Your Own Problem
Consider identical spherical conducting space ships in deep space where
gravitational fields from other bodies are negligible compared to the
gravitational attraction between the ships. Construct a problem in which
you place identical excess charges on the space ships to exactly counter
their gravitational attraction. Calculate the amount of excess charge
needed. Examine whether that charge depends on the distance between
the centers of the ships, the masses of the ships, or any other factors.
Discuss whether this would be an easy, difficult, or even impossible thing
to do in practice.
662 CHAPTER 18 | ELECTRIC CHARGE AND ELECTRIC FIELD
CHAPTER 19 | ELECTRIC POTENTIAL AND ELECTRIC FIELD 663
19
ELECTRIC POTENTIAL AND ELECTRIC FIELD
Figure 19.1 Automated external defibrillator unit (AED) (credit: U.S. Defense Department photo/Tech. Sgt. Suzanne M. Day)
Learning Objectives
19.1. Electric Potential Energy: Potential Difference
• Define electric potential and electric potential energy.
• Describe the relationship between potential difference and electrical potential energy.
• Explain electron volt and its usage in submicroscopic process.
• Determine electric potential energy given potential difference and amount of charge.
19.2. Electric Potential in a Uniform Electric Field
• Describe the relationship between voltage and electric field.
• Derive an expression for the electric potential and electric field.
• Calculate electric field strength given distance and voltage.
19.3. Electrical Potential Due to a Point Charge
• Explain point charges and express the equation for electric potential of a point charge.
• Distinguish between electric potential and electric field.
• Determine the electric potential of a point charge given charge and distance.
19.4. Equipotential Lines
• Explain equipotential lines and equipotential surfaces.
• Describe the action of grounding an electrical appliance.
• Compare electric field and equipotential lines.
19.5. Capacitors and Dielectrics
• Describe the action of a capacitor and define capacitance.
• Explain parallel plate capacitors and their capacitances.
• Discuss the process of increasing the capacitance of a dielectric.
• Determine capacitance given charge and voltage.
19.6. Capacitors in Series and Parallel
• Derive expressions for total capacitance in series and in parallel.
• Identify series and parallel parts in the combination of connection of capacitors.
• Calculate the effective capacitance in series and parallel given individual capacitances.
19.7. Energy Stored in Capacitors
• List some uses of capacitors.
• Express in equation form the energy stored in a capacitor.
• Explain the function of a defibrillator.
664 CHAPTER 19 | ELECTRIC POTENTIAL AND ELECTRIC FIELD
Introduction to Electric Potential and Electric Energy
In Electric Charge and Electric Field, we just scratched the surface (or at least rubbed it) of electrical phenomena. Two of the most familiar aspects of electricity are its energy and voltage. We know, for example, that great amounts of electrical energy can be stored in batteries, are transmitted
cross-country through power lines, and may jump from clouds to explode the sap of trees. In a similar manner, at molecular levels, ions cross cell
membranes and transfer information. We also know about voltages associated with electricity. Batteries are typically a few volts, the outlets in your
home produce 120 volts, and power lines can be as high as hundreds of thousands of volts. But energy and voltage are not the same thing. A
motorcycle battery, for example, is small and would not be very successful in replacing the much larger car battery, yet each has the same voltage. In
this chapter, we shall examine the relationship between voltage and electrical energy and begin to explore some of the many applications of
electricity.
19.1 Electric Potential Energy: Potential Difference
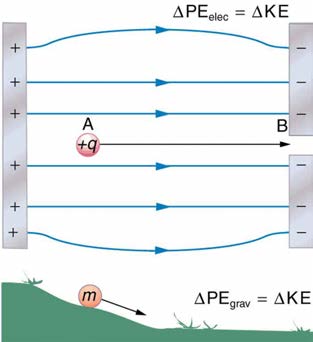
When a free positive charge q is accelerated by an electric field, such as shown in Figure 19.2, it is given kinetic energy. The process is analogous to an object being accelerated by a gravitational field. It is as if the charge is going down an electrical hill where its electric potential energy is
converted to kinetic energy. Let us explore the work done on a charge q by the electric field in this process, so that we may develop a definition of
electric potential energy.
Figure 19.2 A charge accelerated by an electric field is analogous to a mass going down a hill. In both cases potential energy is converted to another form. Work is done by a
force, but since this force is conservative, we can write W = –ΔPE .
The electrostatic or Coulomb force is conservative, which means that the work done on q is independent of the path taken. This is exactly analogous
to the gravitational force in the absence of dissipative forces such as friction. When a force is conservative, it is possible to define a potential energy
associated with the force, and it is usually easier to deal with the potential energy (because it depends only on position) than to calculate the work
directly.
We use the letters PE to denote electric potential energy, which has units of joules (J). The change in potential energy, ΔPE , is crucial, since the
work done by a conservative force is the negative of the change in potential energy; that is, W = –ΔPE . For example, work W done to accelerate
a positive charge from rest is positive and results from a loss in PE, or a negative ΔPE . There must be a minus sign in front of ΔPE to make W
positive. PE can be found at any point by taking one point as a reference and calculating the work needed to move a charge to the other point.
Potential Energy
W = –ΔPE . For example, work W done to accelerate a positive charge from rest is positive and results from a loss in PE, or a negative
ΔPE. There must be a minus sign in front of ΔPE to make W positive. PE can be found at any point by taking one point as a reference and
calculating the work needed to move a charge to the other point.
Gravitational potential energy and electric potential energy are quite analogous. Potential energy accounts for work done by a conservative force and
gives added insight regarding energy and energy transformation without the necessity of dealing with the force directly. It is much more common, for
example, to use the concept of voltage (related to electric potential energy) than to deal with the Coulomb force directly.
Calculating the work directly is generally difficult, since W = Fd cos θ and the direction and magnitude of F can be complex for multiple charges,
for odd-shaped objects, and along arbitrary paths. But we do know that, since F = qE , the work, and hence ΔPE , is proportional to the test
charge q. To have a physical quantity that is independent of test charge, we define electric potential V (or simply potential, since electric is
understood) to be the potential energy per unit charge:
(19.1)
V = PE
q .
Electric Potential
This is the electric potential energy per unit charge.
CHAPTER 19 | ELECTRIC POTENTIAL AND ELECTRIC FIELD 665
(19.2)
V = PE
q
Since PE is proportional to q , the dependence on q cancels. Thus V does not depend on q . The change in potential energy ΔPE is crucial,
and so we are concerned with the difference in potential or potential difference Δ V between two points, where
(19.3)
Δ V = V B − V A = ΔPE
q .
The potential difference between points A and B, V B – V A , is thus defined to be the change in potential energy of a charge q moved from A to
B, divided by the charge. Units of potential difference are joules per coulomb, given the name volt (V) after Alessandro Volta.
(19.4)
1 V = 1 JC
Potential Difference
The potential difference between points A and B, V B - V A , is defined to be the change in potential energy of a charge q moved from A to B,
divided by the charge. Units of potential difference are joules per coulomb, given the name volt (V) after Alessandro Volta.
<












