work.
Internal Energy U
We can think about the internal energy of a system in two different but consistent ways. The first is the atomic and molecular view, which examines
the system on the atomic and molecular scale. The internal energy U of a system is the sum of the kinetic and potential energies of its atoms and
molecules. Recall that kinetic plus potential energy is called mechanical energy. Thus internal energy is the sum of atomic and molecular mechanical
energy. Because it is impossible to keep track of all individual atoms and molecules, we must deal with averages and distributions. A second way to
view the internal energy of a system is in terms of its macroscopic characteristics, which are very similar to atomic and molecular average values.
Macroscopically, we define the change in internal energy Δ U to be that given by the first law of thermodynamics:
(15.2)
Δ U = Q − W.
Many detailed experiments have verified that Δ U = Q − W , where Δ U is the change in total kinetic and potential energy of all atoms and
molecules in a system. It has also been determined experimentally that the internal energy U of a system depends only on the state of the system
and not how it reached that state. More specifically, U is found to be a function of a few macroscopic quantities (pressure, volume, and temperature,
for example), independent of past history such as whether there has been heat transfer or work done. This independence means that if we know the
state of a system, we can calculate changes in its internal energy U from a few macroscopic variables.
Making Connections: Macroscopic and Microscopic
In thermodynamics, we often use the macroscopic picture when making calculations of how a system behaves, while the atomic and molecular
picture gives underlying explanations in terms of averages and distributions. We shall see this again in later sections of this chapter. For
example, in the topic of entropy, calculations will be made using the atomic and molecular view.
To get a better idea of how to think about the internal energy of a system, let us examine a system going from State 1 to State 2. The system has
internal energy U 1 in State 1, and it has internal energy U 2 in State 2, no matter how it got to either state. So the change in internal energy
Δ U = U 2 − U 1 is independent of what caused the change. In other words, Δ U is independent of path. By path, we mean the method of getting
from the starting point to the ending point. Why is this independence important? Note that Δ U = Q − W . Both Q and W depend on path, but
Δ U does not. This path independence means that internal energy U is easier to consider than either heat transfer or work done.
508 CHAPTER 15 | THERMODYNAMICS
Example 15.1 Calculating Change in Internal Energy: The Same Change in U is Produced by Two Different
Processes
(a) Suppose there is heat transfer of 40.00 J to a system, while the system does 10.00 J of work. Later, there is heat transfer of 25.00 J out of the
system while 4.00 J of work is done on the system. What is the net change in internal energy of the system?
(b) What is the change in internal energy of a system when a total of 150.00 J of heat transfer occurs out of (from) the system and 159.00 J of
work is done on the system? (See Figure 15.4).
Strategy
In part (a), we must first find the net heat transfer and net work done from the given information. Then the first law of thermodynamics
⎛⎝Δ U = Q − W⎞⎠ can be used to find the change in internal energy. In part (b), the net heat transfer and work done are given, so the equation
can be used directly.
Solution for (a)
The net heat transfer is the heat transfer into the system minus the heat transfer out of the system, or
Q
(15.3)
= 40.00 J − 25.00 J = 15.00 J.
Similarly, the total work is the work done by the system minus the work done on the system, or
W
(15.4)
= 10.00 J − 4.00 J = 6.00 J.
Thus the change in internal energy is given by the first law of thermodynamics:
(15.5)
Δ U = Q − W = 15.00 J − 6.00 J = 9.00 J.
We can also find the change in internal energy for each of the two steps. First, consider 40.00 J of heat transfer in and 10.00 J of work out, or
(15.6)
Δ U 1 = Q 1 − W 1 = 40.00 J − 10.00 J = 30.00 J.
Now consider 25.00 J of heat transfer out and 4.00 J of work in, or
(15.7)
Δ U 2 = Q 2 − W 2= - 25.00 J − ( − 4.00 J ) = –21.00 J.
The total change is the sum of these two steps, or
(15.8)
Δ U = Δ U 1 + Δ U 2 = 30.00 J + (−21.00 J ) = 9.00 J.
Discussion on (a)
No matter whether you look at the overall process or break it into steps, the change in internal energy is the same.
Solution for (b)
Here the net heat transfer and total work are given directly to be Q = – 150.00 J and W = – 159.00 J , so that
(15.9)
Δ U = Q – W = – 150.00 J – ( − 159.00 J) = 9.00 J.
Discussion on (b)
A very different process in part (b) produces the same 9.00-J change in internal energy as in part (a). Note that the change in the system in both
parts is related to Δ U and not to the individual Q s or W s involved. The system ends up in the same state in both (a) and (b). Parts (a) and
(b) present two different paths for the system to follow between the same starting and ending points, and the change in internal energy for each
is the same—it is independent of path.
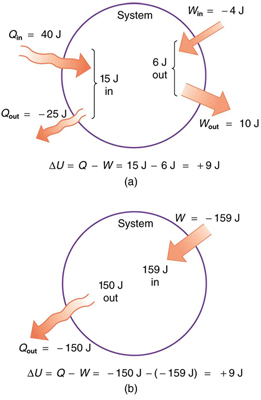
CHAPTER 15 | THERMODYNAMICS 509
Figure 15.4 Two different processes produce the same change in a system. (a) A total of 15.00 J of heat transfer occurs into the system, while work takes out a total of 6.00 J.
The change in internal energy is Δ U = Q − W = 9.00 J . (b) Heat transfer removes 150.00 J from the system while work puts 159.00 J into it, producing an increase of 9.00 J in internal energy. If the system starts out in the same state in (a) and (b), it will end up in the same final state in either case—its final state is related to internal energy, not how that energy was acquired.
Human Metabolism and the First Law of Thermodynamics
Human metabolism is the conversion of food into heat transfer, work, and stored fat. Metabolism is an interesting example of the first law of
thermodynamics in action. We now take another look at these topics via the first law of thermodynamics. Considering the body as the system of
interest, we can use the first law to examine heat transfer, doing work, and internal energy in activities ranging from sleep to heavy exercise. What
are some of the major characteristics of heat transfer, doing work, and energy in the body? For one, body temperature is normally kept constant by
heat transfer to the surroundings. This means Q is negative. Another fact is that the body usually does work on the outside world. This means W is
positive. In such situations, then, the body loses internal energy, since Δ U = Q − W is negative.
Now consider the effects of eating. Eating increases the internal energy of the body by adding chemical potential energy (this is an unromantic view
of a good steak). The body metabolizes all the food we consume. Basically, metabolism is an oxidation process in which the chemical potential
energy of food is released. This implies that food input is in the form of work. Food energy is reported in a special unit, known as the Calorie. This
energy is measured by burning food in a calorimeter, which is how the units are determined.
In chemistry and biochemistry, one calorie (spelled with a lowercase c) is defined as the energy (or heat transfer) required to raise the temperature of
one gram of pure water by one degree Celsius. Nutritionists and weight-watchers tend to use the dietary calorie, which is frequently called a Calorie
(spelled with a capital C). One food Calorie is the energy needed to raise the temperature of one kilogram of water by one degree Celsius. This
means that one dietary Calorie is equal to one kilocalorie for the chemist, and one must be careful to avoid confusion between the two.
Again, consider the internal energy the body has lost. There are three places this internal energy can go—to heat transfer, to doing work, and to
stored fat (a tiny fraction also goes to cell repair and growth). Heat transfer and doing work take internal energy out of the body, and food puts it back.
If you eat just the right amount of food, then your average internal energy remains constant. Whatever you lose to heat transfer and doing work is
replaced by food, so that, in the long run, Δ U = 0 . If you overeat repeatedly, then Δ U is always positive, and your body stores this extra internal
energy as fat. The reverse is true if you eat too little. If Δ U is negative for a few days, then the body metabolizes its own fat to maintain body
temperature and do work that takes energy from the body. This process is how dieting produces weight loss.
Life is not always this simple, as any dieter knows. The body stores fat or metabolizes it only if energy intake changes for a period of several days.
Once you have been on a major diet, the next one is less successful because your body alters the way it responds to low energy intake. Your basal
metabolic rate (BMR) is the rate at which food is converted into heat transfer and work done while the body is at complete rest. The body adjusts its
basal metabolic rate to partially compensate for over-eating or under-eating. The body will decrease the metabolic rate rather than eliminate its own
fat to replace lost food intake. You will chill more easily and feel less energetic as a result of the lower metabolic rate, and you will not lose weight as
fast as before. Exercise helps to lose weight, because it produces both heat transfer from your body and work, and raises your metabolic rate even
when you are at rest. Weight loss is also aided by the quite low efficiency of the body in converting internal energy to work, so that the loss of internal
energy resulting from doing work is much greater than the work done.It should be noted, however, that living systems are not in thermalequilibrium.
The body provides us with an excellent indication that many thermodynamic processes are irreversible. An irreversible process can go in one
direction but not the reverse, under a given set of conditions. For example, although body fat can be converted to do work and produce heat transfer,

510 CHAPTER 15 | THERMODYNAMICS
work done on the body and heat transfer into it cannot be converted to body fat. Otherwise, we could skip lunch by sunning ourselves or by walking
down stairs. Another example of an irreversible thermodynamic process is photosynthesis. This process is the intake of one form of
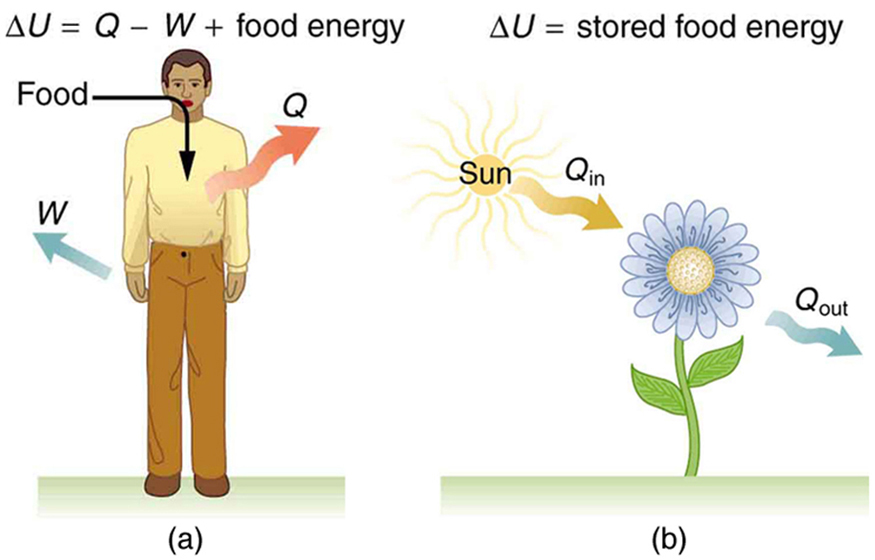
energy—light—by plants and its conversion to chemical potential energy. Both applications of the first law of thermodynamics are illustrated in Figure
15.5. One great advantage of conservation laws such as the first law of thermodynamics is that they accurately describe the beginning and ending
points of complex processes, such as metabolism and photosynthesis, without regard to the complications in between. Table 15.1 presents a
summary of terms relevant to the first law of thermodynamics.
Figure 15.5 (a) The first law of thermodynamics applied to metabolism. Heat transferred out of the body ( Q ) and work done by the body ( W ) remove internal energy, while food intake replaces it. (Food intake may be considered as work done on the body.) (b) Plants convert part of the radiant heat transfer in sunlight to stored chemical energy, a
process called photosynthesis.
Table 15.1 Summary of Terms for the First Law of Thermodynamics, ΔU=Q−W
Term
Definition
Internal energy—the sum of the kinetic and potential energies of a system’s atoms and molecules. Can be divided into many
U
subcategories, such as thermal and chemical energy. Depends only on the state of a system (such as its P , V , and T ), not on how the
energy entered the system. Change in internal energy is path independent.
Q
Heat—energy transferred because of a temperature difference. Characterized by random molecular motion. Highly dependent on path.
Q entering a system is positive.
W
Work—energy transferred by a force moving through a distance. An organized, orderly process. Path dependent. W done by a system
(either against an external force or to increase the volume of the system) is positive.
15.2 The First Law of Thermodynamics and Some Simple Processes
Figure 15.6 Beginning with the Industrial Revolution, humans have harnessed power through the use of the first law of thermodynamics, before we even understood it
completely. This photo, of a steam engine at the Turbinia Works, dates from 1911, a mere 61 years after the first explicit statement of the first law of thermodynamics by
Rudolph Clausius. (credit: public domain; author unknown)
One of the most important things we can do with heat transfer is to use it to do work for us. Such a device is called a heat engine. Car engines and
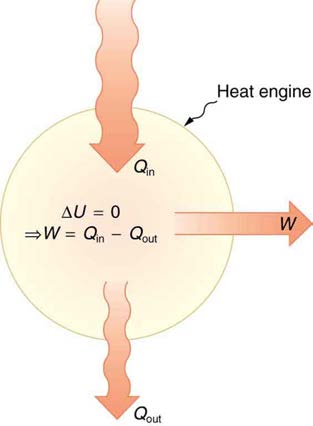
steam turbines that generate electricity are examples of heat engines. Figure 15.7 shows schematically how the first law of thermodynamics applies
to the typical heat engine.
CHAPTER 15 | THERMODYNAMICS 511
Figure 15.7 Schematic representation of a heat engine, governed, of course, by the first law of thermodynamics. It is impossible to devise a system where Q out = 0 , that is, in which no heat transfer occurs to the environment.
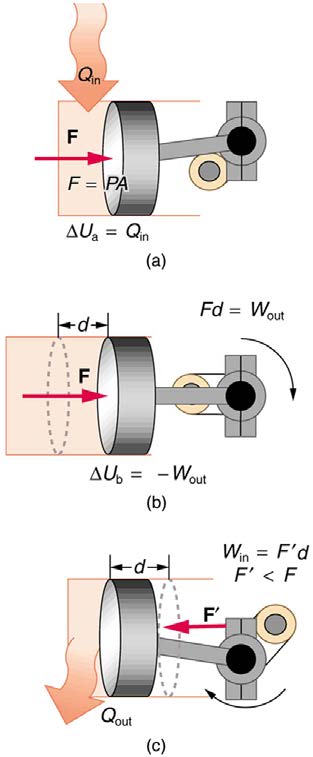
Figure 15.8 (a) Heat transfer to the gas in a cylinder increases the internal energy of the gas, creating higher pressure and temperature. (b) The force exerted on the movable
cylinder does work as the gas expands. Gas pressure and temperature decrease when it expands, indicating that the gas’s internal energy has been decreased by doing work.
(c) Heat transfer to the environment further reduces pressure in the gas so that the piston can be more easily returned to its starting position.
The illustrations above show one of the ways in which heat transfer does work. Fuel combustion produces heat transfer to a gas in a cylinder,
increasing the pressure of the gas and thereby the force it exerts on a movable piston. The gas does work on the outside world, as this force moves
the piston through some distance. Heat transfer to the gas cylinder results in work being done. To repeat this process, the piston needs to be returned
to its starting point. Heat transfer now occurs from the gas to the surroundings so that its pressure decreases, and a force is exerted by the
surroundings to push the piston back through some distance. Variations of this process are employed daily in hundreds of millions of heat engines.
We will examine heat engines in detail in the next section. In this section, we consider some of the simpler underlying processes on which heat
engines are based.
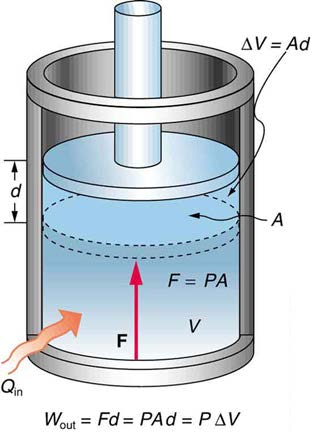
512 CHAPTER 15 | THERMODYNAMICS
PV Diagrams and their Relationship to Work Done on or by a Gas
A process by which a gas does work on a piston at constant pressure is called an isobaric process. Since the pressure is constant, the force
exerted is constant and the work done is given as
P
(15.10)
Δ V.
Figure 15.9 An isobaric expansion of a gas requires heat transfer to keep the pressure constant. Since pressure is constant, the work done is PΔ V .
W
(15.11)
= Fd
See the symbols as shown in Figure 15.9. Now F = PA , and so
W
(15.12)
= PAd.
Because the volume of a cylinder is its cross-sectional area A times its length d , we see that Ad = Δ V , the change in volume; thus,
W
(15.13)
= PΔ V (isobaric process).
Note that if Δ V is positive, then W is positive, meaning that work is done by the gas on the outside world.
(Note that the pressure involved in this work that we’ve called P is the pressure of the gas inside the tank. If we call the pressure outside the tank
P ext , an expanding gas would be working against the external pressure; the work done would therefore be W = − P extΔ V (isobaric process).
Many texts use this definition of work, and not the definition based on internal pressure, as the basis of the First Law of Thermodynamics. This
definition reverses the sign conventions for work, and results in a statement of the first law that becomes Δ U = Q + W .)
It is not surprising that W = PΔ V , since we have already noted in our treatment of fluids that pressure is a type of potential energy per unit volume
and that pressure in fact has units of energy divided by volume. We also noted in our discussion of the ideal gas law that PV has units of energy. In
this case, some of the energy associated with pressure becomes work.
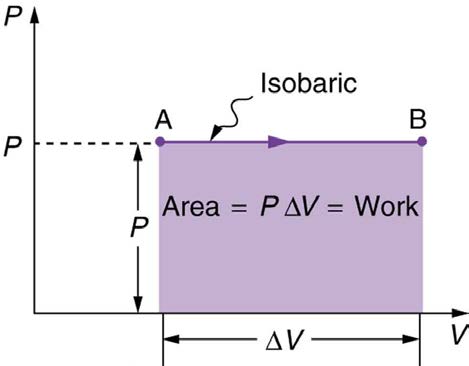
Figure 15.10 shows a graph of pressure versus volume (that is, a PV diagram for an isobaric process. You can see in the figure that the work done is the area under the graph. This property of PV diagrams is very useful and broadly applicable: the work done on or by a system in going from one
state to another equals the area under the curve on a PV diagram.
CHAPTER 15 | THERMODYNAMICS 513
Figure 15.10 A graph of pressure versus volume for a constant-pressure, or isobaric, process, such as the one shown in Figure 15.9. The area under the curve equals the
work done by the gas, since W = PΔ V .
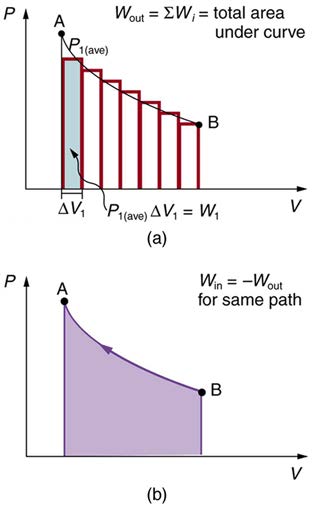
Figure 15.11 (a) A PV diagram in which pressure varies as well as volume. The work done for each interval is its average pressure times the change in volume, or the area under the curve over that interval. Thus the total area under the curve equals the total work done. (b) Work must be done on the system to follow the reverse path. This is
interpreted as a negative area under the curve.
We can see where this leads by considering Figure 15.11(a), which shows a more general process in which both pressure and volume change. The
area under the curve is closely approximated by dividing it into strips, each having an average constant pressure Pi(ave) . The work done is
Wi = Pi(ave)Δ Vi for each strip, and the total work done is the sum of the Wi . Thus the total work done is the total area under the curve. If the path is reversed, as in Figure 15.11(b), then work is done on the system. The area under the curve in that case is negative, because Δ V is negative.
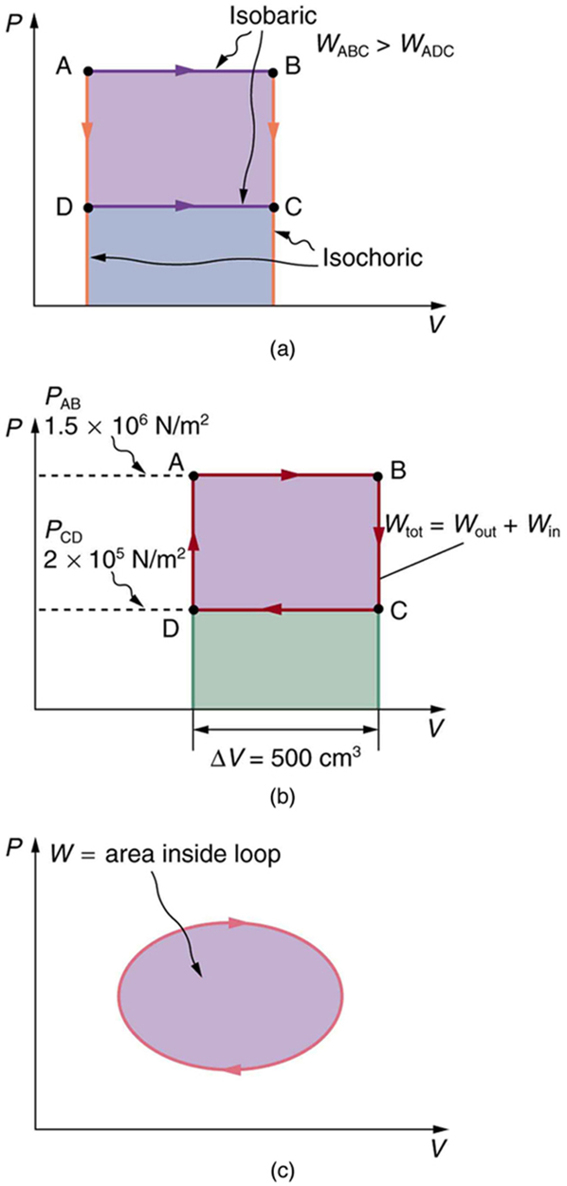
PV diagrams clearly illustrate that the work done depends on the path taken and not just the endpoints. This path dependence is seen in Figure
15.12(a), where more work is done in going from A to C by the path via point B than by the path via point D. The vertical paths, where volume is
constant, are called isochoric processes. Since volume is constant, Δ V = 0 , and no work is done in an isochoric process. Now, if the system
follows the cyclical path ABCDA, as in Figure 15.12(b), then the total work done is the area inside the loop. The negative area below path CD
subtracts, leaving only the area inside the rectangle. In fact, the work done in any cyclical process (one that returns to its starting point) is the area
inside the loop it forms on a PV diagram, as Figure 15.12(c) illustrates for a general cyclical process. Note that the loop must be traversed in the
clockwise direction for work to be positive—that is, for there to be a net work output.
514 CHAPTER 15 | THERMODYNAMICS
Figure 15.12 (a) The work done in going from A to C depends on path. The work is greater for the path ABC than for the path ADC, because the former is at higher pressure.
In both cases, the work done is the area under the path. This area is greater for path ABC. (b) The total work done in the cyclical process ABCDA is the area inside the loop,
since the negative area below CD subtracts out, leaving just the area inside the rectangle. (The values given for the pressures and the change in volume are intended for use
in the example below.) (c) The area inside any closed loop is the work done in the cyclical process. If the loop is traversed in a clockwise direction, W is positive—it is work done on the outside environment. If the loop is traveled in a counter-clockwise direction, W is negative—it is work that is done to the system.
Example 15.2 Total Work Done in a Cyclical Process Equals the Area Inside the Closed Loop on a PV Diagram
Calculate the total work done in the cyclical process ABCDA shown in Figure 15.12(b) by the following two methods to verify that work equals
the area inside the closed loop on the PV diagram. (Take the data in the figure to be precise to three significant figures.) (a) Calculate the work
done along each segment of the path and add these values to get the total work. (b) Calculate the area inside the rectangle ABCDA.
Strategy
To find the work along any path on a PV diagram, you use the fact that work is pressure times change in volume, or W = PΔ V . So in part
(a), this value is calculated for each leg of the path around the closed loop.
Solution for (a)
The work along path AB is
W
(15.14)
AB = P ABΔ V AB
= (1.50 × 106 N/m2)(5.00 × 10–4 m3 ) = 750 J.
Since the path BC is isochoric, Δ V BC = 0 , and so W BC = 0 . The work along path CD is negative, since Δ V CD is negative (the volume
decreases). The work is
CHAPTER 15 | THERMODYNAMICS 515
W
(15.15)
CD = P CDΔ V CD
= (2.00












