⎝1.38×10−23 J/K⎞⎠(273 K)
Discussion
This number is undeniably large, considering that a gas is mostly empty space. N is huge, even in small volumes. For example, 1 cm3 of a
gas at STP has 2.68×1019 molecules in it. Once again, note that N is the same for all types or mixtures of gases.
Moles and Avogadro’s Number
It is sometimes convenient to work with a unit other than molecules when measuring the amount of substance. A mole (abbreviated mol) is defined to
be the amount of a substance that contains as many atoms or molecules as there are atoms in exactly 12 grams (0.012 kg) of carbon-12. The actual
number of atoms or molecules in one mole is called Avogadro’s number ( N A) , in recognition of Italian scientist Amedeo Avogadro (1776–1856).
He developed the concept of the mole, based on the hypothesis that equal volumes of gas, at the same pressure and temperature, contain equal
numbers of molecules. That is, the number is independent of the type of gas. This hypothesis has been confirmed, and the value of Avogadro’s
number is
(13.28)
N A = 6.02×1023 mol−1.
Avogadro’s Number
One mole always contains 6.02×1023 particles (atoms or molecules), independent of the element or substance. A mole of any substance has
a mass in grams equal to its molecular mass, which can be calculated from the atomic masses given in the periodic table of elements.
(13.29)
N A = 6.02×1023 mol−1
CHAPTER 13 | TEMPERATURE, KINETIC THEORY, AND THE GAS LAWS 445
Figure 13.19 How big is a mole? On a macroscopic level, one mole of table tennis balls would cover the Earth to a depth of about 40 km.
Check Your Understanding
The active ingredient in a Tylenol pill is 325 mg of acetaminophen (C8 H9 NO2) . Find the number of active molecules of acetaminophen in a
single pill.
Solution
We first need to calculate the molar mass (the mass of one mole) of acetaminophen. To do this, we need to multiply the number of atoms of each
element by the element’s atomic mass.
(13.30)
(8 moles of carbon)(12 grams/mole) + (9 moles hydrogen)(1 gram/mole)
+(1 mole nitrogen)(14 grams/mole) + (2 moles oxygen)(16 grams/mole) = 151 g
Then we need to calculate the number of moles in 325 mg.
(13.31)
⎛
325 mg
⎞⎛ 1 gram ⎞
⎝151 grams/mole⎠⎝1000 mg⎠ = 2.15×10−3 moles
Then use Avogadro’s number to calculate the number of molecules.
⎛
(13.32)
N = ⎛⎝2.15×10−3 moles⎞⎠⎝6.02×1023 molecules/mole⎞⎠ = 1.30×1021 molecules
Example 13.8 Calculating Moles per Cubic Meter and Liters per Mole
Calculate: (a) the number of moles in 1.00 m3 of gas at STP, and (b) the number of liters of gas per mole.
Strategy and Solution
(a) We are asked to find the number of moles per cubic meter, and we know from Example 13.7 that the number of molecules per cubic meter at
STP is 2.68×1025 . The number of moles can be found by dividing the number of molecules by Avogadro’s number. We let n stand for the
number of moles,
(13.33)
n mol/m3 =
N molecules/m3
= 2.68×1025 molecules/m3 = 44.5 mol/m3 .
6.02×1023 molecules/mol 6.02×1023 molecules/mol
(b) Using the value obtained for the number of moles in a cubic meter, and converting cubic meters to liters, we obtain
⎛
(13.34)
⎝103 L/m3⎞⎠
44.5 mol/m3 = 22.5 L/mol.
Discussion
This value is very close to the accepted value of 22.4 L/mol. The slight difference is due to rounding errors caused by using three-digit input.
Again this number is the same for all gases. In other words, it is independent of the gas.
The (average) molar weight of air (approximately 80% N2 and 20% O2 is M = 28.8 g. Thus the mass of one cubic meter of air is 1.28 kg. If
a living room has dimensions 5 m×5 m×3 m, the mass of air inside the room is 96 kg, which is the typical mass of a human.
Check Your Understanding
The density of air at standard conditions ( P = 1 atm and T = 20ºC) is 1.28 kg/m3 . At what pressure is the density 0.64 kg/m3 if the
temperature and number of molecules are kept constant?
Solution
446 CHAPTER 13 | TEMPERATURE, KINETIC THEORY, AND THE GAS LAWS
The best way to approach this question is to think about what is happening. If the density drops to half its original value and no molecules are
lost, then the volume must double. If we look at the equation PV = NkT , we see that when the temperature is constant, the pressure is
inversely proportional to volume. Therefore, if the volume doubles, the pressure must drop to half its original value, and P f = 0.50 atm.
The Ideal Gas Law Restated Using Moles
A very common expression of the ideal gas law uses the number of moles, n , rather than the number of atoms and molecules, N . We start from the
ideal gas law,
PV
(13.35)
= NkT,
and multiply and divide the equation by Avogadro’s number N A . This gives
(13.36)
PV = N
N N
A A kT.
Note that n = N / N A is the number of moles. We define the universal gas constant R = N A k , and obtain the ideal gas law in terms of moles.
Ideal Gas Law (in terms of moles)
The ideal gas law (in terms of moles) is
PV
(13.37)
= nRT.
The numerical value of R in SI units is
⎛
(13.38)
R = N A k = ⎛⎝6.02×1023 mol−1⎞⎠⎝1.38×10−23 J/K⎞⎠ = 8.31 J / mol ⋅ K.
In other units,
R
(13.39)
= 1.99 cal/mol ⋅ K
R = 0.0821 L ⋅ atm/mol ⋅ K.
You can use whichever value of R is most convenient for a particular problem.
Example 13.9 Calculating Number of Moles: Gas in a Bike Tire
How many moles of gas are in a bike tire with a volume of 2.00×10 – 3 m3(2.00 L) , a pressure of 7.00×105 Pa (a gauge pressure of just
under 90.0 lb/in2 ), and at a temperature of 18.0ºC ?
Strategy
Identify the knowns and unknowns, and choose an equation to solve for the unknown. In this case, we solve the ideal gas law, PV = nRT , for
the number of moles n .
Solution
1. Identify the knowns.
(13.40)
P = 7.00×105 Pa
V = 2.00×10−3 m3
T = 18.0ºC = 291 K
R = 8.31 J/mol ⋅ K
2. Rearrange the equation to solve for n and substitute known values.
⎛
⎛
(13.41)
n = PV
⎝7.00×105 Pa⎞⎠⎝2.00×10−3 m3⎞⎠
RT =
(8.31 J/mol ⋅ K)(291 K)
= 0.579 mol
Discussion
The most convenient choice for R in this case is 8.31 J/mol ⋅ K, because our known quantities are in SI units. The pressure and temperature
are obtained from the initial conditions in Example 13.6, but we would get the same answer if we used the final values.
The ideal gas law can be considered to be another manifestation of the law of conservation of energy (see Conservation of Energy). Work done on
a gas results in an increase in its energy, increasing pressure and/or temperature, or decreasing volume. This increased energy can also be viewed
as increased internal kinetic energy, given the gas’s atoms and molecules.
CHAPTER 13 | TEMPERATURE, KINETIC THEORY, AND THE GAS LAWS 447
The Ideal Gas Law and Energy
Let us now examine the role of energy in the behavior of gases. When you inflate a bike tire by hand, you do work by repeatedly exerting a force
through a distance. This energy goes into increasing the pressure of air inside the tire and increasing the temperature of the pump and the air.
The ideal gas law is closely related to energy: the units on both sides are joules. The right-hand side of the ideal gas law in PV = NkT is NkT .
This term is roughly the amount of translational kinetic energy of N atoms or molecules at an absolute temperature T , as we shall see formally in
Kinetic Theory: Atomic and Molecular Explanation of Pressure and Temperature. The left-hand side of the ideal gas law is PV , which also has the units of joules. We know from our study of fluids that pressure is one type of potential energy per unit volume, so pressure multiplied by volume is
energy. The important point is that there is energy in a gas related to both its pressure and its volume. The energy can be changed when the gas is
doing work as it expands—something we explore in Heat and Heat Transfer Methods—similar to what occurs in gasoline or steam engines and
turbines.
Problem-Solving Strategy: The Ideal Gas Law
Step 1 Examine the situation to determine that an ideal gas is involved. Most gases are nearly ideal.
Step 2 Make a list of what quantities are given, or can be inferred from the problem as stated (identify the known quantities). Convert known
values into proper SI units (K for temperature, Pa for pressure, m3 for volume, molecules for N , and moles for n ).
Step 3 Identify exactly what needs to be determined in the problem (identify the unknown quantities). A written list is useful.
Step 4 Determine whether the number of molecules or the number of moles is known, in order to decide which form of the ideal gas law to use.
The first form is PV = NkT and involves N , the number of atoms or molecules. The second form is PV = nRT and involves n , the number of moles.
Step 5 Solve the ideal gas law for the quantity to be determined (the unknown quantity). You may need to take a ratio of final states to initial
states to eliminate the unknown quantities that are kept fixed.
Step 6 Substitute the known quantities, along with their units, into the appropriate equation, and obtain numerical solutions complete with units.
Be certain to use absolute temperature and absolute pressure.
Step 7 Check the answer to see if it is reasonable: Does it make sense?
Check Your Understanding
Liquids and solids have densities about 1000 times greater than gases. Explain how this implies that the distances between atoms and
molecules in gases are about 10 times greater than the size of their atoms and molecules.
Solution
Atoms and molecules are close together in solids and liquids. In gases they are separated by empty space. Thus gases have lower densities
than liquids and solids. Density is mass per unit volume, and volume is related to the size of a body (such as a sphere) cubed. So if the distance
between atoms and molecules increases by a factor of 10, then the volume occupied increases by a factor of 1000, and the density decreases
by a factor of 1000.
13.4 Kinetic Theory: Atomic and Molecular Explanation of Pressure and Temperature
We have developed macroscopic definitions of pressure and temperature. Pressure is the force divided by the area on which the force is exerted, and
temperature is measured with a thermometer. We gain a better understanding of pressure and temperature from the kinetic theory of gases, which
assumes that atoms and molecules are in continuous random motion.
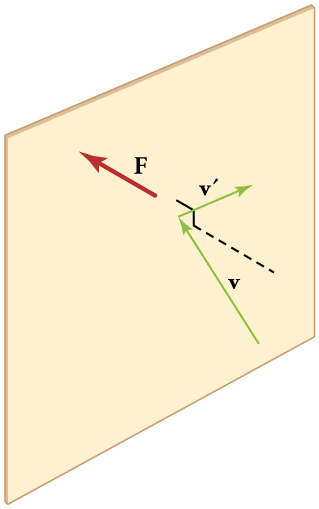
448 CHAPTER 13 | TEMPERATURE, KINETIC THEORY, AND THE GAS LAWS
Figure 13.20 When a molecule collides with a rigid wall, the component of its momentum perpendicular to the wall is reversed. A force is thus exerted on the wall, creating
pressure.
Figure 13.20 shows an elastic collision of a gas molecule with the wall of a container, so that it exerts a force on the wall (by Newton’s third law).
Because a huge number of molecules will collide with the wall in a short time, we observe an average force per unit area. These collisions are the
source of pressure in a gas. As the number of molecules increases, the number of collisions and thus the pressure increase. Similarly, the gas
pressure is higher if the average velocity of molecules is higher. The actual relationship is derived in the Things Great and Small feature below. The following relationship is found:
(13.42)
PV = 13 Nmv 2 ,
where P is the pressure (average force per unit area), V is the volume of gas in the container, N is the number of molecules in the container, m
is the mass of a molecule, and v 2 is the average of the molecular speed squared.
What can we learn from this atomic and molecular version of the ideal gas law? We can derive a relationship between temperature and the average
translational kinetic energy of molecules in a gas. Recall the previous expression of the ideal gas law:
PV
(13.43)
= NkT.
Equating the right-hand side of this equation with the right-hand side of PV = 13 Nmv 2 gives
(13.44)
13 Nmv 2 = NkT.
Making Connections: Things Great and Small—Atomic and Molecular Origin of Pressure in a Gas
Figure 13.21 shows a box filled with a gas. We know from our previous discussions that putting more gas into the box produces greater
pressure, and that increasing the temperature of the gas also produces a greater pressure. But why should increasing the temperature of the gas
increase the pressure in the box? A look at the atomic and molecular scale gives us some answers, and an alternative expression for the ideal
gas law.
The figure shows an expanded view of an elastic collision of a gas molecule with the wall of a container. Calculating the average force exerted by
such molecules will lead us to the ideal gas law, and to the connection between temperature and molecular kinetic energy. We assume that a
molecule is small compared with the separation of molecules in the gas, and that its interaction with other molecules can be ignored. We also
assume the wall is rigid and that the molecule’s direction changes, but that its speed remains constant (and hence its kinetic energy and the
magnitude of its momentum remain constant as well). This assumption is not always valid, but the same result is obtained with a more detailed
description of the molecule’s exchange of energy and momentum with the wall.
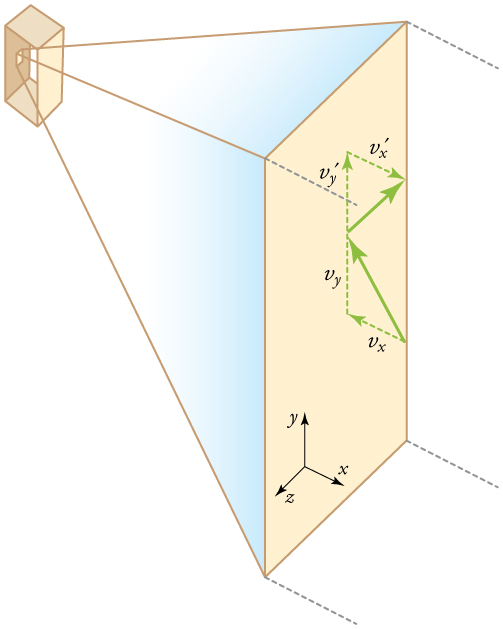
CHAPTER 13 | TEMPERATURE, KINETIC THEORY, AND THE GAS LAWS 449
Figure 13.21 Gas in a box exerts an outward pressure on its walls. A molecule colliding with a rigid wall has the direction of its velocity and momentum in the x -direction reversed. This direction is perpendicular to the wall. The components of its velocity momentum in the y - and z -directions are not changed, which means there is no
force parallel to the wall.
If the molecule’s velocity changes in the x -direction, its momentum changes from –mvx to + mvx . Thus, its change in momentum is
Δ mv = + mvx–( –mvx) = 2 mvx . The force exerted on the molecule is given by
(13.45)
F = Δ p
Δ t = 2 mvx
Δ t .
There is no force between the wall and the molecule until the molecule hits the wall. During the short time of the collision, the force between the
molecule and wall is relatively large. We are looking for an average force; we take Δ t to be the average time between collisions of the molecule
with this wall. It is the time it would take the molecule to go across the box and back (a distance 2 l) at a speed of vx . Thus Δ t = 2 l / vx , and the expression for the force becomes
2
(13.46)
F = 2 mvx
2 l / v = mvx
x
l .
This force is due to one molecule. We multiply by the number of molecules N and use their average squared velocity to find the force
(13.47)
2
F = Nmvx
l ,
where the bar over a quantity means its average value. We would like to have the force in terms of the speed v , rather than the x -component
of the velocity. We note that the total velocity squared is the sum of the squares of its components, so that
(13.48)
v 2 = v 2
2
2
x + vy + vz.
Because the velocities are random, their average components in all directions are the same:
(13.49)
v 2
2
2
x = vy = vz.
Thus,
(13.50)
v 2 = 3 v 2 x,
or
(13.51)
v 2 x = 13 v 2.
Substituting 1
3 v 2 into the expression for F gives
450 CHAPTER 13 | TEMPERATURE, KINETIC THEORY, AND THE GAS LAWS
(13.52)
F = Nmv 2
3 l .
The pressure is F / A, so that we obtain
(13.53)
P = F
Nmv 2
A = Nmv 2
3 Al = 13 V ,
where we used V = Al for the volume. This gives the important result.
(13.54)
PV = 13 Nmv 2
This equation is another expression of the ideal gas law.
We can get the average kinetic energy of a molecule, 1
2 mv 2 , from the left-hand side of the equation by canceling N and multiplying by 3/2. This
calculation produces the result that the average kinetic energy of a molecule is directly related to absolute temperature.
(13.55)
KE = 12 mv 2 = 32 kT
The average translational kinetic energy of a molecule, KE , is called thermal energy. The equation KE = 12 mv 2 = 32 kT is a molecular
interpretation of temperature, and it has been found to be valid for gases and reasonably accurate in liquids and solids. It is another definition of
temperature based on an expression of the molecular energy.
It is sometimes useful to rearrange KE = 12 mv 2 = 32 kT , and solve for the average speed of molecules in a gas in terms of temperature,
(13.56)
v 2 = v rms = 3 kT
m ,
where v rms stands for root-mean-square (rms) speed.
Example 13.10 Calculating Kinetic Energy and Speed of a Gas Molecule
(a) What is the average kinetic energy of a gas molecule at 20.0ºC (room temperature)? (b) Find the rms speed of a nitrogen molecule (N2)
at this temperature.
Strategy for (a)
The known in the equation for the average kinetic energy is the temperature.
(13.57)
KE = 12 mv 2 = 32 kT
Before substituting values into this equation, we must convert the given temperature to kelvins. This conversion gives
T = (20.0 + 273) K = 293 K.
Solution for (a)
The temperature alone is sufficient to find the average translational kinetic energy. Substituting the temperature into the translational kinetic
energy equation gives
(13.58)
KE = 3
⎛
2 kT = 32⎝1.38×10−23 J/K⎞⎠(293 K) = 6.07×10−21 J.
Strategy for (b)
Finding the rms speed of a nitrogen molecule involves a straightforward calculation using the equation
(13.59)
v 2 = v rms = 3 kT
m ,
but we must first find the mass of a nitrogen molecule. Using the molecular mass of nitrogen N2 from the periodic table,
(13.60)
m = 2(14.0067)×10−3 kg/mol
6.02×1023 mol−1
= 4.65×10−26 kg.
Solution for (b)
CHAPTER 13 | TEMPERATURE, KINETIC THEORY, AND THE GAS LAWS 451
Substituting this mass and the value for k into the equation for v rms yields
(13.61)
3⎛
v
⎝1.38×10 – 23 J/K⎞⎠(293 K)
rms = 3 kT
m =
= 511 m/s.
4.65×10–26 kg
Discussion
Note that the average kinetic energy of the molecule is independent of the type of molecule. The average translational kinetic energy depends
only on absolute temperature. The kinetic energy is very small compared to macroscopic energies, so that we do not feel when an air molecule is
hitting our skin. The rms velocity of the nitrogen molecule is surprisingly large. These large molecular velocities do not yield macroscopic
movement of air, since the molecules move in all directions with equal likelihood. The mean free path (the distance a molecule can move on
average between collisions) of molecules in air is very small, and so the molecules move rapidly but do not get very far in a second. The high
value for rms speed is reflected in the speed of sound, however, which is about 340 m/s at room temperature. The faster the rms speed of air
molecules, the faster that sound vibrations can be transferred through the air. The speed of sound increases with temperature and is greater in
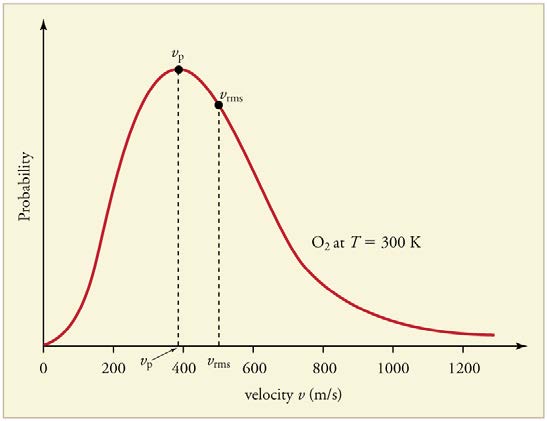
gases with small molecular masses, such as helium. (See Figure 13.22.)
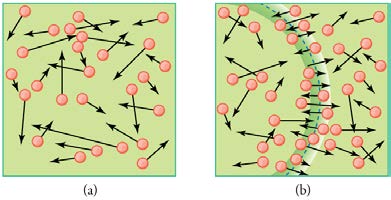
Figure 13.22 (a) There are many molecules moving so fast in an ordinary gas that they coll








