Secrecy was endemic. Alchemists discovered and rediscovered many facts but did not make them broadly available. As the Middle Ages ended,
alchemy gradually faded, and the science of chemistry arose. It was no longer possible, nor considered desirable, to keep discoveries secret.
Collective knowledge grew, and by the beginning of the 19th century, an important fact was well established—the masses of reactants in specific
chemical reactions always have a particular mass ratio. This is very strong indirect evidence that there are basic units (atoms and molecules) that
have these same mass ratios. The English chemist John Dalton (1766–1844) did much of this work, with significant contributions by the Italian
physicist Amedeo Avogadro (1776–1856). It was Avogadro who developed the idea of a fixed number of atoms and molecules in a mole, and this
special number is called Avogadro’s number in his honor. The Austrian physicist Johann Josef Loschmidt was the first to measure the value of the
constant in 1865 using the kinetic theory of gases.
Patterns and Systematics
The recognition and appreciation of patterns has enabled us to make many discoveries. The periodic table of elements was proposed as an
organized summary of the known elements long before all elements had been discovered, and it led to many other discoveries. We shall see in
later chapters that patterns in the properties of subatomic particles led to the proposal of quarks as their underlying structure, an idea that is still
bearing fruit.
Knowledge of the properties of elements and compounds grew, culminating in the mid-19th-century development of the periodic table of the elements
by Dmitri Mendeleev (1834–1907), the great Russian chemist. Mendeleev proposed an ingenious array that highlighted the periodic nature of the
properties of elements. Believing in the systematics of the periodic table, he also predicted the existence of then-unknown elements to complete it.
Once these elements were discovered and determined to have properties predicted by Mendeleev, his periodic table became universally accepted.
Also during the 19th century, the kinetic theory of gases was developed. Kinetic theory is based on the existence of atoms and molecules in random
thermal motion and provides a microscopic explanation of the gas laws, heat transfer, and thermodynamics (see Introduction to Temperature,
Kinetic Theory, and the Gas Laws and Introduction to Laws of Thermodynamics). Kinetic theory works so well that it is another strong indication of the existence of atoms. But it is still indirect evidence—individual atoms and molecules had not been observed. There were heated debates about
the validity of kinetic theory until direct evidence of atoms was obtained.
The first truly direct evidence of atoms is credited to Robert Brown, a Scottish botanist. In 1827, he noticed that tiny pollen grains suspended in still
water moved about in complex paths. This can be observed with a microscope for any small particles in a fluid. The motion is caused by the random
thermal motions of fluid molecules colliding with particles in the fluid, and it is now called Brownian motion. (See Figure 30.2.) Statistical fluctuations in the numbers of molecules striking the sides of a visible particle cause it to move first this way, then that. Although the molecules cannot be directly
observed, their effects on the particle can be. By examining Brownian motion, the size of molecules can be calculated. The smaller and more
numerous they are, the smaller the fluctuations in the numbers striking different sides.


CHAPTER 30 | ATOMIC PHYSICS 1065
Figure 30.2 The position of a pollen grain in water, measured every few seconds under a microscope, exhibits Brownian motion. Brownian motion is due to fluctuations in the
number of atoms and molecules colliding with a small mass, causing it to move about in complex paths. This is nearly direct evidence for the existence of atoms, providing a
satisfactory alternative explanation cannot be found.
It was Albert Einstein who, starting in his epochal year of 1905, published several papers that explained precisely how Brownian motion could be
used to measure the size of atoms and molecules. (In 1905 Einstein created special relativity, proposed photons as quanta of EM radiation, and
produced a theory of Brownian motion that allowed the size of atoms to be determined. All of this was done in his spare time, since he worked days
as a patent examiner. Any one of these very basic works could have been the crowning achievement of an entire career—yet Einstein did even more
in later years.) Their sizes were only approximately known to be 10−10 m , based on a comparison of latent heat of vaporization and surface
tension made in about 1805 by Thomas Young of double-slit fame and the famous astronomer and mathematician Simon Laplace.
Using Einstein’s ideas, the French physicist Jean-Baptiste Perrin (1870–1942) carefully observed Brownian motion; not only did he confirm Einstein’s
theory, he also produced accurate sizes for atoms and molecules. Since molecular weights and densities of materials were well established, knowing
atomic and molecular sizes allowed a precise value for Avogadro’s number to be obtained. (If we know how big an atom is, we know how many fit
into a certain volume.) Perrin also used these ideas to explain atomic and molecular agitation effects in sedimentation, and he received the 1926
Nobel Prize for his achievements. Most scientists were already convinced of the existence of atoms, but the accurate observation and analysis of
Brownian motion was conclusive—it was the first truly direct evidence.
A huge array of direct and indirect evidence for the existence of atoms now exists. For example, it has become possible to accelerate ions (much as
electrons are accelerated in cathode-ray tubes) and to detect them individually as well as measure their masses (see More Applications of
Magnetism for a discussion of mass spectrometers). Other devices that observe individual atoms, such as the scanning tunneling electron
microscope, will be discussed elsewhere. (See Figure 30.3.) All of our understanding of the properties of matter is based on and consistent with the atom. The atom’s substructures, such as electron shells and the nucleus, are both interesting and important. The nucleus in turn has a substructure,
as do the particles of which it is composed. These topics, and the question of whether there is a smallest basic structure to matter, will be explored in
later parts of the text.
Figure 30.3 Individual atoms can be detected with devices such as the scanning tunneling electron microscope that produced this image of individual gold atoms on a graphite
substrate. (credit: Erwin Rossen, Eindhoven University of Technology, via Wikimedia Commons)
30.2 Discovery of the Parts of the Atom: Electrons and Nuclei
Just as atoms are a substructure of matter, electrons and nuclei are substructures of the atom. The experiments that were used to discover electrons
and nuclei reveal some of the basic properties of atoms and can be readily understood using ideas such as electrostatic and magnetic force, already
covered in previous chapters.
Charges and Electromagnetic Forces
In previous discussions, we have noted that positive charge is associated with nuclei and negative charge with electrons. We have also covered
many aspects of the electric and magnetic forces that affect charges. We will now explore the discovery of the electron and nucleus as
substructures of the atom and examine their contributions to the properties of atoms.

1066 CHAPTER 30 | ATOMIC PHYSICS
The Electron
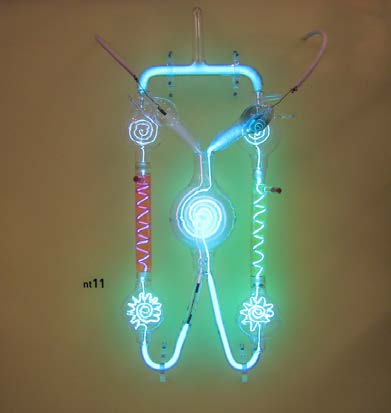
Gas discharge tubes, such as that shown in Figure 30.4, consist of an evacuated glass tube containing two metal electrodes and a rarefied gas.
When a high voltage is applied to the electrodes, the gas glows. These tubes were the precursors to today’s neon lights. They were first studied
seriously by Heinrich Geissler, a German inventor and glassblower, starting in the 1860s. The English scientist William Crookes, among others,
continued to study what for some time were called Crookes tubes, wherein electrons are freed from atoms and molecules in the rarefied gas inside
the tube and are accelerated from the cathode (negative) to the anode (positive) by the high potential. These “cathode rays” collide with the gas
atoms and molecules and excite them, resulting in the emission of electromagnetic (EM) radiation that makes the electrons’ path visible as a ray that
spreads and fades as it moves away from the cathode.
Gas discharge tubes today are most commonly called cathode-ray tubes, because the rays originate at the cathode. Crookes showed that the
electrons carry momentum (they can make a small paddle wheel rotate). He also found that their normally straight path is bent by a magnet in the
direction expected for a negative charge moving away from the cathode. These were the first direct indications of electrons and their charge.
Figure 30.4 A gas discharge tube glows when a high voltage is applied to it. Electrons emitted from the cathode are accelerated toward the anode; they excite atoms and
molecules in the gas, which glow in response. Once called Geissler tubes and later Crookes tubes, they are now known as cathode-ray tubes (CRTs) and are found in older
TVs, computer screens, and x-ray machines. When a magnetic field is applied, the beam bends in the direction expected for negative charge. (credit: Paul Downey, Flickr)
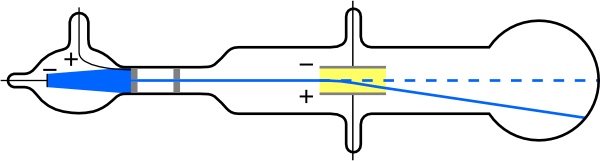
The English physicist J. J. Thomson (1856–1940) improved and expanded the scope of experiments with gas discharge tubes. (See Figure 30.5 and
Figure 30.6.) He verified the negative charge of the cathode rays with both magnetic and electric fields. Additionally, he collected the rays in a metal cup and found an excess of negative charge. Thomson was also able to measure the ratio of the charge of the electron to its mass, qe / me —an
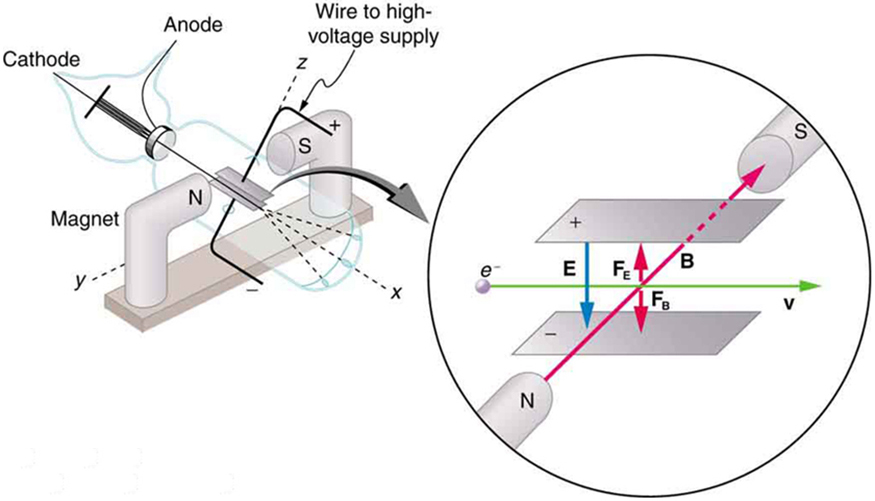
important step to finding the actual values of both qe and me . Figure 30.7 shows a cathode-ray tube, which produces a narrow beam of electrons that passes through charging plates connected to a high-voltage power supply. An electric field E is produced between the charging plates, and the
cathode-ray tube is placed between the poles of a magnet so that the electric field E is perpendicular to the magnetic field B of the magnet. These
fields, being perpendicular to each other, produce opposing forces on the electrons. As discussed for mass spectrometers in More Applications of
Magnetism, if the net force due to the fields vanishes, then the velocity of the charged particle is v = E / B . In this manner, Thomson determined the velocity of the electrons and then moved the beam up and down by adjusting the electric field.
Figure 30.5 J. J. Thomson (credit: www.firstworldwar.com, via Wikimedia Commons)
CHAPTER 30 | ATOMIC PHYSICS 1067
Figure 30.6 Diagram of Thomson’s CRT. (credit: Kurzon, Wikimedia Commons)
Figure 30.7 This schematic shows the electron beam in a CRT passing through crossed electric and magnetic fields and causing phosphor to glow when striking the end of the
tube.
To see how the amount of deflection is used to calculate qe / me , note that the deflection is proportional to the electric force on the electron:
F
(30.1)
= qeE.
But the vertical deflection is also related to the electron’s mass, since the electron’s acceleration is
(30.2)
a = F
m .
e
The value of F is not known, since qe was not yet known. Substituting the expression for electric force into the expression for acceleration yields
(30.3)
a = F
m = qe E.
e
me
Gathering terms, we have
qe
(30.4)
m = a
e
E.
q
The deflection is analyzed to get a , and E is determined from the applied voltage and distance between the plates; thus,
e
me can be determined.
q
With the velocity known, another measurement of
e
me can be obtained by bending the beam of electrons with the magnetic field. Since
F mag = qevB = mea , we have qe / me = a / vB . Consistent results are obtained using magnetic deflection.
What is so important about qe / me , the ratio of the electron’s charge to its mass? The value obtained is
qe
(30.5)
m = −1.76×1011 C/kg (electron).
e
This is a huge number, as Thomson realized, and it implies that the electron has a very small mass. It was known from electroplating that about
108 C/kg is needed to plate a material, a factor of about 1000 less than the charge per kilogram of electrons. Thomson went on to do the same
experiment for positively charged hydrogen ions (now known to be bare protons) and found a charge per kilogram about 1000 times smaller than that
for the electron, implying that the proton is about 1000 times more massive than the electron. Today, we know more precisely that
qp
(30.6)
m = 9.57×107 C/kg(proton),
p
where q p is the charge of the proton and m p is its mass. This ratio (to four significant figures) is 1836 times less charge per kilogram than for the
electron. Since the charges of electrons and protons are equal in magnitude, this implies m p = 1836 me .
Thomson performed a variety of experiments using differing gases in discharge tubes and employing other methods, such as the photoelectric effect,
for freeing electrons from atoms. He always found the same properties for the electron, proving it to be an independent particle. For his work, the

1068 CHAPTER 30 | ATOMIC PHYSICS
important pieces of which he began to publish in 1897, Thomson was awarded the 1906 Nobel Prize in Physics. In retrospect, it is difficult to
appreciate how astonishing it was to find that the atom has a substructure. Thomson himself said, “It was only when I was convinced that the
experiment left no escape from it that I published my belief in the existence of bodies smaller than atoms.”
Thomson attempted to measure the charge of individual electrons, but his method could determine its charge only to the order of magnitude
expected.
Since Faraday’s experiments with electroplating in the 1830s, it had been known that about 100,000 C per mole was needed to plate singly ionized
ions. Dividing this by the number of ions per mole (that is, by Avogadro’s number), which was approximately known, the charge per ion was
calculated to be about 1.6×10−19 C , close to the actual value.
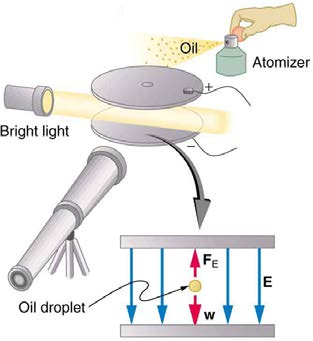
An American physicist, Robert Millikan (1868–1953) (see Figure 30.8), decided to improve upon Thomson’s experiment for measuring qe and was eventually forced to try another approach, which is now a classic experiment performed by students. The Millikan oil drop experiment is shown in
Figure 30.9.
Figure 30.8 Robert Millikan (credit: Unknown Author, via Wikimedia Commons)
Figure 30.9 The Millikan oil drop experiment produced the first accurate direct measurement of the charge on electrons, one of the most fundamental constants in nature. Fine
drops of oil become charged when sprayed. Their movement is observed between metal plates with a potential applied to oppose the gravitational force. The balance of
gravitational and electric forces allows the calculation of the charge on a drop. The charge is found to be quantized in units of −1.6×10−19 C , thus determining directly
the charge of the excess and missing electrons on the oil drops.
In the Millikan oil drop experiment, fine drops of oil are sprayed from an atomizer. Some of these are charged by the process and can then be
suspended between metal plates by a voltage between the plates. In this situation, the weight of the drop is balanced by the electric force:
m
(30.7)
drop g = qeE
The electric field is produced by the applied voltage, hence, E = V / d , and V is adjusted to just balance the drop’s weight. The drops can be seen
as points of reflected light using a microscope, but they are too small to directly measure their size and mass. The mass of the drop is determined by
observing how fast it falls when the voltage is turned off. Since air resistance is very significant for these submicroscopic drops, the more massive
drops fall faster than the less massive, and sophisticated sedimentation calculations can reveal their mass. Oil is used rather than water, because it
does not readily evaporate, and so mass is nearly constant. Once the mass of the drop is known, the charge of the electron is given by rearranging
the previous equation:
m
m
(30.8)
q = drop g
drop gd
E
=
V
,
where d is the separation of the plates and V is the voltage that holds the drop motionless. (The same drop can be observed for several hours to
see that it really is motionless.) By 1913 Millikan had measured the charge of the electron qe to an accuracy of 1%, and he improved this by a factor
CHAPTER 30 | ATOMIC PHYSICS 1069
of 10 within a few years to a value of −1.60×10−19 C . He also observed that all charges were multiples of the basic electron charge and that
sudden changes could occur in which electrons were added or removed from the drops. For this very fundamental direct measurement of qe and for
his studies of the photoelectric effect, Millikan was awarded the 1923 Nobel Prize in Physics.
With the charge of the electron known and the charge-to-mass ratio known, the electron’s mass can be calculated. It is
(30.9)
m = qe
⎛ q .
e ⎞
⎝ me⎠
Substituting known values yields
(30.10)
me = −1.60×10−19 C
−1.76×1011 C/kg
or
(30.11)
me = 9.11×10−31 kg (electron’s mass),
where the round-off errors have been corrected. The mass of the electron has been verified in many subsequent experiments and is now known to an
accuracy of better than one part in one million. It is an incredibly small mass and remains the smallest known mass of any particle that has mass.
(Some particles, such as photons, are massless and cannot be brought to rest, but travel at the speed of light.) A similar calculation gives the masses
of other particles, including the proton. To three digits, the mass of the proton is now known to be
(30.12)
mp = 1.67×10−27 kg (proton’s mass),
which is nearly identical to the mass of a hydrogen atom. What Thomson and Millikan had done was to prove the existence of one substructure of
atoms, the electron, and further to show that it had only a tiny fraction of the mass of an atom. The nucleus of an atom contains most of its mass, and
the nature of the nucleus was completely unanticipated.
Another important characteristic of quantum mechanics was also beginning to emerge. All electrons are identical to one another. The charge and
mass of electrons are not average values; rather, they are unique values that all electrons have. This is true of other fundamental entities at the
submicroscopic level. All protons are identical to one another, and so on.
The Nucleus
Here, we examine the first direct evidence of the size and mass of the nucleus. In later chapters, we will examine many other aspects of nuclear
physics, but the basic information on nuclear size and mass is so important to understanding the atom that we consider it here.
Nuclear radioactivity was discovered in 1896, and it was soon the subject of intense study by a number of the best scientists in the world. Among
them was New Zealander Lord Ernest Rutherford, who made numerous fundamental discoveries and earned the title of “father of nuclear physics.”
Born in Nelson, Rutherford did his postgraduate studies at the Cavendish Laboratories in England before taking up a position at McGill University in
Canada where he did the work that earned him a Nobel Prize in Chemistry in 1908. In the area of atomic and nuclear physics, there is much overlap
between chemistry and physics, with physics providing the fundamental enabling theories. He returned to England in later years and had six future
Nobel Prize winners as students. Rutherford used nuclear radiation to directly examine the size and mass of the atomic nucleus. The experiment he
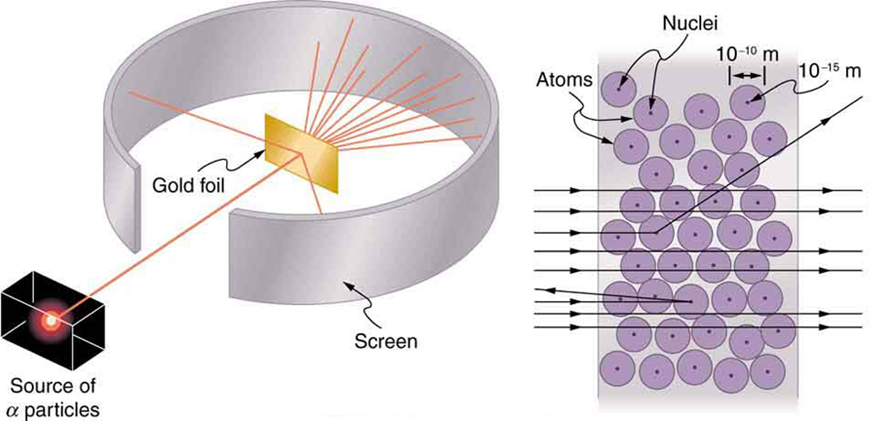
devised is shown in Figure 30.10. A radioactive source that emits alpha radiation was placed in a lead container with a hole in one side to produce a beam of alpha particles, which are a type of ionizing radiation ejected by the nuclei of a radioactive source. A thin gold foil was placed in the beam,
and the scattering of the alpha particles was observed by the glow they caused when they struck a phosphor screen.
Figure 30.10 Rutherford’s experiment gave direct evidence for the size and mass of the nucleus by scattering alpha particles from a thin gold foil. Alpha particles with energies of about 5 MeV are emitted from a radioactive source (which is a small metal container in which a specific amount of a radioactive material is sealed), are collimated into a
beam, and fall upon the foil. The number of particles that penetrate the foil or scatter to various angles indicates that gold nuclei are very small and contain nearly all of the
gold atom’s mass. This is particularly indicated by the alpha particles that scatter to very large angles, much like a soccer ball bouncing off a goalie’s head.
Alpha particles were known to be the doubly charged positive nuclei of helium atoms that had kinetic energies on the order of 5 MeV when emitted
in nuclear decay, which is the disintegration of the nucleus of an unstable nuclide by the spontaneous emission of charged particles. These particles
interact with matter mostly via the Coulomb force, and the manner in which they scatter from nuclei can reveal nuclear size and mass. This is
analogous to observing how a bowling ball is scattered by an object you cannot see directly. Because the alpha particle’s energy is so large
compared with the typical energies associated with atoms ( MeV versus eV ), you would expect the alpha particles to simply crash through a thin
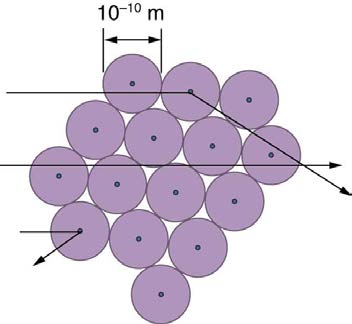
1070 CHAPTER 30 | ATOMIC PHYSICS
foil much like a supersonic bowling ball would crash through a few dozen rows of bowling pins. Thomson had envisioned the atom to be a small
sphere in which equal amounts of positive and negative charge were distributed evenly. The incident massive alpha particles would suffer only small
deflections in such a model. Instead, Rutherford and his collaborators found that alpha particles occasionally were scattered to large angles, some
even back in the direction from which they came! Detailed analysis using conservation of momentum and energy—particularly of the small number
that came straight back—implied that gold nuclei are very small compared with the size of a gold atom, contain almost all of the atom’s mass, and are
tightly bound. Since the gold nucleus is several times more massive than the alpha particle, a














