314 CHAPTER 9 | STATICS AND TORQUE
Figure 9.38 The knee joint works like a hinge to bend and straighten the lower leg. It
permits a person to sit, stand, and pivot.
Figure 9.40
29. A device for exercising the upper leg muscle is shown in Figure 9.39,
together with a schematic representation of an equivalent lever system.
31. We analyzed the biceps muscle example with the angle between
Calculate the force exerted by the upper leg muscle to lift the mass at a
forearm and upper arm set at 90º . Using the same numbers as in
constant speed. Explicitly show how you follow the steps in the Problem-
Example 9.4, find the force exerted by the biceps muscle when the angle
Solving Strategy for static equilibrium in Applications of Statistics,
is 120º and the forearm is in a downward position.
Including Problem-Solving Strategies.
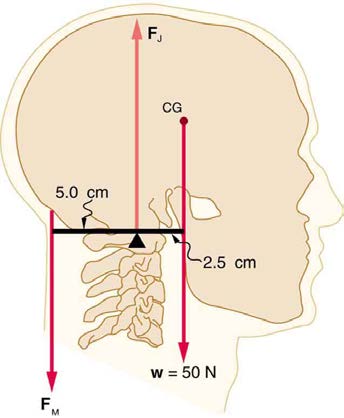
32. Even when the head is held erect, as in Figure 9.41, its center of
mass is not directly over the principal point of support (the atlanto-
occipital joint). The muscles at the back of the neck should therefore
exert a force to keep the head erect. That is why your head falls forward
when you fall asleep in the class. (a) Calculate the force exerted by these
muscles using the information in the figure. (b) What is the force exerted
by the pivot on the head?
Figure 9.39 A mass is connected by pulleys and wires to the ankle in this exercise
device.
30. A person working at a drafting board may hold her head as shown in
Figure 9.40, requiring muscle action to support the head. The three
major acting forces are shown. Calculate the direction and magnitude of
Figure 9.41 The center of mass of the head lies in front of its major point of support,
the force supplied by the upper vertebrae FV to hold the head
requiring muscle action to hold the head erect. A simplified lever system is shown.
stationary, assuming that this force acts along a line through the center of
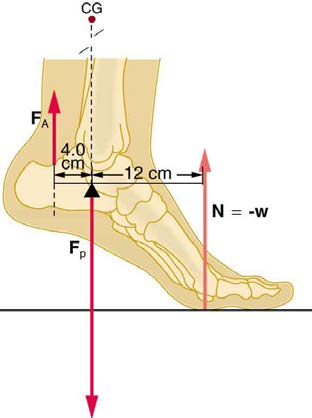
33. A 75-kg man stands on his toes by exerting an upward force through
mass as do the weight and muscle force.
the Achilles tendon, as in Figure 9.42. (a) What is the force in the
Achilles tendon if he stands on one foot? (b) Calculate the force at the
pivot of the simplified lever system shown—that force is representative of
forces in the ankle joint.
CHAPTER 9 | STATICS AND TORQUE 315
36. Integrated Concepts
Suppose we replace the 4.0-kg book in Exercise 9.31 of the biceps
muscle with an elastic exercise rope that obeys Hooke’s Law. Assume its
force constant k = 600 N/m . (a) How much is the rope stretched (past
equilibrium) to provide the same force F B as in this example? Assume
the rope is held in the hand at the same location as the book. (b) What
force is on the biceps muscle if the exercise rope is pulled straight up so
that the forearm makes an angle of 25º with the horizontal? Assume the
biceps muscle is still perpendicular to the forearm.
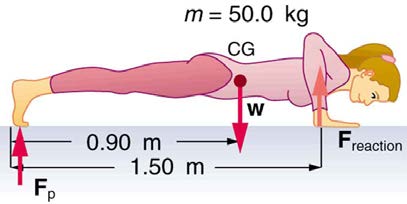
37. (a) What force should the woman in Figure 9.45 exert on the floor
with each hand to do a push-up? Assume that she moves up at a
constant speed. (b) The triceps muscle at the back of her upper arm has
an effective lever arm of 1.75 cm, and she exerts force on the floor at a
horizontal distance of 20.0 cm from the elbow joint. Calculate the
magnitude of the force in each triceps muscle, and compare it to her
weight. (c) How much work does she do if her center of mass rises 0.240
m? (d) What is her useful power output if she does 25 pushups in one
minute?
Figure 9.42 The muscles in the back of the leg pull the Achilles tendon when one
stands on one’s toes. A simplified lever system is shown.
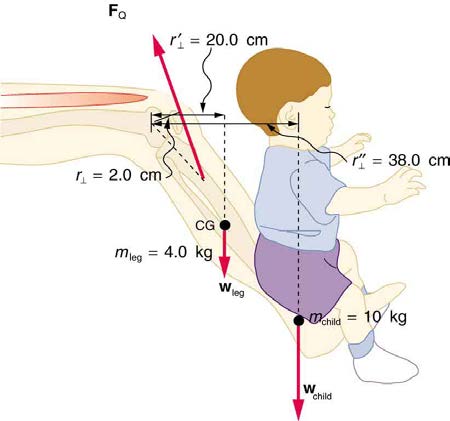
34. A father lifts his child as shown in Figure 9.43. What force should the
upper leg muscle exert to lift the child at a constant speed?
Figure 9.45 A woman doing pushups.
38. You have just planted a sturdy 2-m-tall palm tree in your front lawn for
your mother’s birthday. Your brother kicks a 500 g ball, which hits the top
of the tree at a speed of 5 m/s and stays in contact with it for 10 ms. The
ball falls to the ground near the base of the tree and the recoil of the tree
is minimal. (a) What is the force on the tree? (b) The length of the sturdy
section of the root is only 20 cm. Furthermore, the soil around the roots is
loose and we can assume that an effective force is applied at the tip of
the 20 cm length. What is the effective force exerted by the end of the tip
of the root to keep the tree from toppling? Assume the tree will be
uprooted rather than bend. (c) What could you have done to ensure that
the tree does not uproot easily?
39. Unreasonable Results
Suppose two children are using a uniform seesaw that is 3.00 m long and
has its center of mass over the pivot. The first child has a mass of 30.0
Figure 9.43 A child being lifted by a father’s lower leg.
kg and sits 1.40 m from the pivot. (a) Calculate where the second 18.0 kg
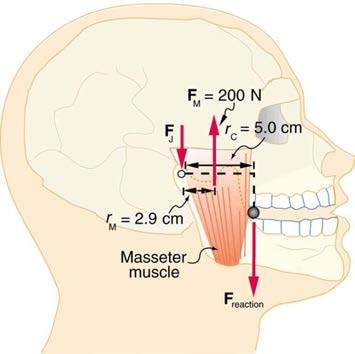
35. Unlike most of the other muscles in our bodies, the masseter muscle
child must sit to balance the seesaw. (b) What is unreasonable about the
in the jaw, as illustrated in Figure 9.44, is attached relatively far from the
result? (c) Which premise is unreasonable, or which premises are
joint, enabling large forces to be exerted by the back teeth. (a) Using the
inconsistent?
information in the figure, calculate the force exerted by the teeth on the
40. Construct Your Own Problem
bullet. (b) Calculate the force on the joint.
Consider a method for measuring the mass of a person’s arm in
anatomical studies. The subject lies on her back, extends her relaxed
arm to the side and two scales are placed below the arm. One is placed
under the elbow and the other under the back of her hand. Construct a
problem in which you calculate the mass of the arm and find its center of
mass based on the scale readings and the distances of the scales from
the shoulder joint. You must include a free body diagram of the arm to
direct the analysis. Consider changing the position of the scale under the
hand to provide more information, if needed. You may wish to consult
references to obtain reasonable mass values.
Figure 9.44 A person clenching a bullet between his teeth.
316 CHAPTER 9 | STATICS AND TORQUE

CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM 317
10
ROTATIONAL MOTION AND ANGULAR
MOMENTUM
Figure 10.1 The mention of a tornado conjures up images of raw destructive power. Tornadoes blow houses away as if they were made of paper and have been known to
pierce tree trunks with pieces of straw. They descend from clouds in funnel-like shapes that spin violently, particularly at the bottom where they are most narrow, producing
winds as high as 500 km/h. (credit: Daphne Zaras, U.S. National Oceanic and Atmospheric Administration)
Learning Objectives
10.1. Angular Acceleration
• Describe uniform circular motion.
• Explain non-uniform circular motion.
• Calculate angular acceleration of an object.
• Observe the link between linear and angular acceleration.
10.2. Kinematics of Rotational Motion
• Observe the kinematics of rotational motion.
• Derive rotational kinematic equations.
• Evaluate problem solving strategies for rotational kinematics.
10.3. Dynamics of Rotational Motion: Rotational Inertia
• Understand the relationship between force, mass and acceleration.
• Study the turning effect of force.
• Study the analogy between force and torque, mass and moment of inertia, and linear acceleration and angular acceleration.
10.4. Rotational Kinetic Energy: Work and Energy Revisited
• Derive the equation for rotational work.
• Calculate rotational kinetic energy.
• Demonstrate the Law of Conservation of Energy.
10.5. Angular Momentum and Its Conservation
• Understand the analogy between angular momentum and linear momentum.
• Observe the relationship between torque and angular momentum.
• Apply the law of conservation of angular momentum.
10.6. Collisions of Extended Bodies in Two Dimensions
• Observe collisions of extended bodies in two dimensions.
• Examine collision at the point of percussion.
10.7. Gyroscopic Effects: Vector Aspects of Angular Momentum
• Describe the right-hand rule to find the direction of angular velocity, momentum, and torque.
• Explain the gyroscopic effect.
• Study how Earth acts like a gigantic gyroscope.

318 CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM
Introduction to Rotational Motion and Angular Momentum
Why do tornadoes spin at all? And why do tornados spin so rapidly? The answer is that air masses that produce tornadoes are themselves rotating,
and when the radii of the air masses decrease, their rate of rotation increases. An ice skater increases her spin in an exactly analogous manner as
seen in Figure 10.2. The skater starts her rotation with outstretched limbs and increases her spin by pulling them in toward her body. The same
physics describes the exhilarating spin of a skater and the wrenching force of a tornado.
Clearly, force, energy, and power are associated with rotational motion. These and other aspects of rotational motion are covered in this chapter. We
shall see that all important aspects of rotational motion either have already been defined for linear motion or have exact analogs in linear motion.
First, we look at angular acceleration—the rotational analog of linear acceleration.
Figure 10.2 This figure skater increases her rate of spin by pulling her arms and her extended leg closer to her axis of rotation. (credit: Luu, Wikimedia Commons)
10.1 Angular Acceleration
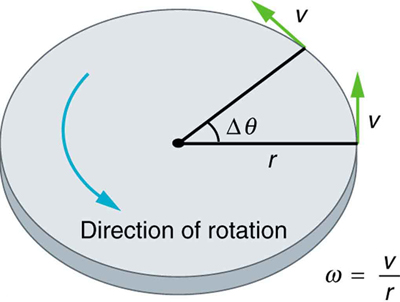
Uniform Circular Motion and Gravitation discussed only uniform circular motion, which is motion in a circle at constant speed and, hence, constant
angular velocity. Recall that angular velocity ω was defined as the time rate of change of angle θ :
(10.1)
ω = Δ θ
Δ t ,
where θ is the angle of rotation as seen in Figure 10.3. The relationship between angular velocity ω and linear velocity v was also defined in
Rotation Angle and Angular Velocity as
v = rω
(10.2)
or
(10.3)
ω = vr,
where r is the radius of curvature, also seen in Figure 10.3. According to the sign convention, the counter clockwise direction is considered as
positive direction and clockwise direction as negative
Figure 10.3 This figure shows uniform circular motion and some of its defined quantities.
Angular velocity is not constant when a skater pulls in her arms, when a child starts up a merry-go-round from rest, or when a computer’s hard disk
slows to a halt when switched off. In all these cases, there is an angular acceleration, in which ω changes. The faster the change occurs, the
greater the angular acceleration. Angular acceleration α is defined as the rate of change of angular velocity. In equation form, angular acceleration is
expressed as follows:
(10.4)
α = Δ ω
Δ t ,
CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM 319
where Δ ω is the change in angular velocity and Δ t is the change in time. The units of angular acceleration are (rad/s)/s , or rad/s2 . If ω
increases, then α is positive. If ω decreases, then α is negative.
Example 10.1 Calculating the Angular Acceleration and Deceleration of a Bike Wheel
Suppose a teenager puts her bicycle on its back and starts the rear wheel spinning from rest to a final angular velocity of 250 rpm in 5.00 s. (a)
Calculate the angular acceleration in rad/s2 . (b) If she now slams on the brakes, causing an angular acceleration of – 87.3 rad/s2 , how long
does it take the wheel to stop?
Strategy for (a)
The angular acceleration can be found directly from its definition in α = Δ ω
Δ t because the final angular velocity and time are given. We see that
Δ ω is 250 rpm and Δ t is 5.00 s.
Solution for (a)
Entering known information into the definition of angular acceleration, we get
(10.5)
α = Δ ω
Δ t
= 250 rpm
5.00 s .
Because Δ ω is in revolutions per minute (rpm) and we want the standard units of rad/s2 for angular acceleration, we need to convert Δ ω
from rpm to rad/s:
(10.6)
Δ ω = 250 rev
min ⋅ 2π rad
rev ⋅ 1 min
60 sec
= 26.2rad
s .
Entering this quantity into the expression for α , we get
(10.7)
α = Δ ω
Δ t
= 26.2 rad/s
5.00 s
= 5.24 rad/s2.
Strategy for (b)
In this part, we know the angular acceleration and the initial angular velocity. We can find the stoppage time by using the definition of angular
acceleration and solving for Δ t , yielding
(10.8)
Δ t = Δ ω
α .
Solution for (b)
Here the angular velocity decreases from 26.2 rad/s (250 rpm) to zero, so that Δ ω is – 26.2 rad/s , and α is given to be – 87.3 rad/s2 .
Thus,
(10.9)
Δ t = – 26.2 rad/s
– 87.3 rad/s2
= 0.300 s.
Discussion
Note that the angular acceleration as the girl spins the wheel is small and positive; it takes 5 s to produce an appreciable angular velocity. When
she hits the brake, the angular acceleration is large and negative. The angular velocity quickly goes to zero. In both cases, the relationships are
analogous to what happens with linear motion. For example, there is a large deceleration when you crash into a brick wall—the velocity change
is large in a short time interval.
If the bicycle in the preceding example had been on its wheels instead of upside-down, it would first have accelerated along the ground and then
come to a stop. This connection between circular motion and linear motion needs to be explored. For example, it would be useful to know how linear
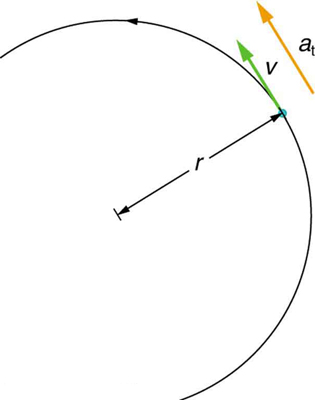
and angular acceleration are related. In circular motion, linear acceleration is tangent to the circle at the point of interest, as seen in Figure 10.4.
Thus, linear acceleration is called tangential acceleration a t .
320 CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM
Figure 10.4 In circular motion, linear acceleration a , occurs as the magnitude of the velocity changes: a is tangent to the motion. In the context of circular motion, linear acceleration is also called tangential acceleration a t .
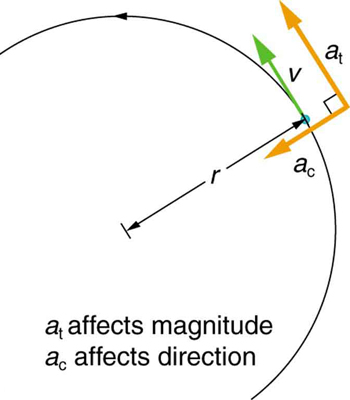
Linear or tangential acceleration refers to changes in the magnitude of velocity but not its direction. We know from Uniform Circular Motion and
Gravitation that in circular motion centripetal acceleration, a c , refers to changes in the direction of the velocity but not its magnitude. An object undergoing circular motion experiences centripetal acceleration, as seen in Figure 10.5. Thus, a t and a c are perpendicular and independent of one another. Tangential acceleration a t is directly related to the angular acceleration α and is linked to an increase or decrease in the velocity, but
not its direction.
Figure 10.5 Centripetal acceleration a c occurs as the direction of velocity changes; it is perpendicular to the circular motion. Centripetal and tangential acceleration are thus perpendicular to each other.
Now we can find the exact relationship between linear acceleration a t and angular acceleration α . Because linear acceleration is proportional to a
change in the magnitude of the velocity, it is defined (as it was in One-Dimensional Kinematics) to be
(10.10)
a t = Δ v
Δ t .
For circular motion, note that v = rω , so that
(10.11)
a t = Δ( rω)
Δ t .
The radius r is constant for circular motion, and so Δ( rω) = r(Δ ω) . Thus,
(10.12)
a t = rΔ ω
Δ t .
By definition, α = Δ ω
Δ t . Thus,
a
(10.13)
t = rα,
or
(10.14)
α = a t r.
These equations mean that linear acceleration and angular acceleration are directly proportional. The greater the angular acceleration is, the larger
the linear (tangential) acceleration is, and vice versa. For example, the greater the angular acceleration of a car’s drive wheels, the greater the
acceleration of the car. The radius also matters. For example, the smaller a wheel, the smaller its linear acceleration for a given angular acceleration
α .
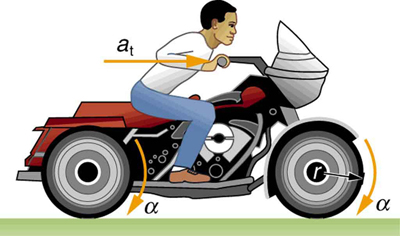
CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM 321
Example 10.2 Calculating the Angular Acceleration of a Motorcycle Wheel
A powerful motorcycle can accelerate from 0 to 30.0 m/s (about 108 km/h) in 4.20 s. What is the angular acceleration of its 0.320-m-radius
wheels? (See Figure 10.6.)
Figure 10.6 The linear acceleration of a motorcycle is accompanied by an angular acceleration of its wheels.
Strategy
We are given information about the linear velocities of the motorcycle. Thus, we can find its linear acceleration a t . Then, the expression
α = a t r can be used to find the angular acceleration.
Solution
The linear acceleration is
(10.15)
a t = Δ v
Δ t
= 30.0 m/s
4.20 s
= 7.14 m/s2.
We also know the radius of the wheels. Entering the values for a t and r into α = a t r , we get
(10.16)
α = a t r
= 7.14 m/s2
0.320 m
= 22.3 rad/s2.
Discussion
Units of radians are dimensionless and appear in any relationship between angular and linear quantities.
So far, we have defined three rotational quantities— θ, ω , and α . These quantities are analogous to the translational quantities x, v , and a .
Table 10.1 displays rotational quantities, the analogous translational quantities, and the relationships between them.
Table 10.1 Rotational and Translational
Quantities
Rotational
Translational
Relationship
θ
x
θ = xr
ω
v
ω = vr
α
a
α = atr
Making Connections: Take-Home Experiment
Sit down with your feet on the ground on a chair that rotates. Lift one of your legs such that it is unbent (straightened out). Using the other leg,
begin to rotate yourself by pushing on the ground. Stop using your leg to push the ground but allow the chair to rotate. From the origin where you
began, sketch the angle, angular velocity, and angular acceleration of your leg as a function of time in the form of three separate graphs.
Estimate the magnitudes of these quantities.
Check Your Understanding
Angular acceleration is a vector, having both magnitude and direction. How do we denote its magnitude and direction? Illustrate with an example.
Solution

322 CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM
The magnitude of angular acceleration is α and its most common units are rad/s2 . The direction o















