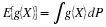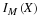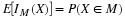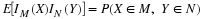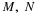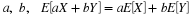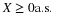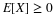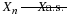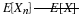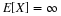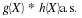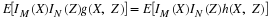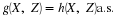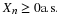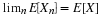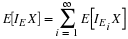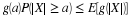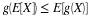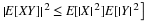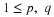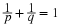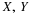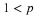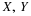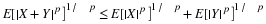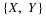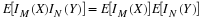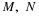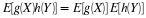A fundamental problem in elementary probability is to find the probability of a logical (Boolean) combination of a finite class of events, when the probabilities of certain other combinations are known. If we partition an event F into component events whose probabilities can be determined, then the additivity property implies the probability of F is the sum of these component probabilities. Frequently, the event F is a Boolean combination of members of a finite class– say, or . For each such finite class, there is a fundamental partition determined by the class. The members of this partition are called minterms. Any Boolean combination of members of the class can be expressed as the disjoint union of a unique subclass of the minterms. If the probability of every minterm in this subclass can be determined, then by additivity the probability of the Boolean combination is determined. We examine these ideas in more detail.

To see how the fundamental partition arises naturally, consider first the partition of the basic space produced by a single event A.

Now if B is a second event, then

(2.2)

The pair 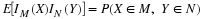has partitioned Ω into 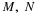. Continuation is this way leads systematically to a partition by three events 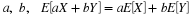, four events 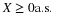, etc.

We illustrate the fundamental patterns in the case of four events 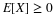. We form the minterms as intersections of members of the class, with various patterns of complementation. For a class of four events, there are 2⁴=16 such patterns, hence 16 minterms. These are, in a systematic arrangement,

Table 2.1.

AcBcCcDc	AcB CcDc	A BcCcDc	A B CcDc
AcBcCcD	AcB CcD	A BcCcD	A B CcD

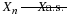
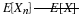
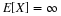
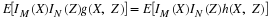
No element can be in more than one minterm, because each differs from the others by complementation of at least one member event. Each element ω is assigned to exactly one of the minterms by determining the answers to four questions:

Is it in A? Is it in B? Is it in C? Is it in D?

Suppose, for example, the answers are: Yes, No, No, Yes. Then ω is in the minterm AB^cC^cD. In a similar way, we can determine the membership of each ω in the basic space. Thus, the minterms form a partition. That is, the minterms represent mutually exclusive events, one of which is sure to occur on each trial. The membership of any minterm depends upon the membership of each generating set 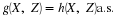or D, and the relationships between them. For some classes, one or more of the minterms are empty (impossible events). As we see below, this causes no problems.

An examination of the development above shows that if we begin with a class of n events, there are 2ⁿ minterms. To aid in systematic handling, we introduce a simple numbering system for the minterms, which we illustrate by considering again the four events 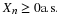, in that order. The answers to the four questions above can be represented numerically by the scheme

No ∼0 and Yes ∼1

Thus, if ω is in A^cB^cC^cD^c, the answers are tabulated as 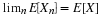. If ω is in AB^cC^cD, then this is designated 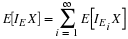. With this scheme, the minterm arrangement above becomes

We may view these quadruples of zeros and ones as binary representations of integers, which may also be represented by their decimal equivalents, as shown in the table. Frequently, it is useful to refer to the minterms by number. If the members of the generating class are treated in a fixed order, then each minterm number arrived at in the manner above specifies a minterm uniquely. Thus, for the generating class 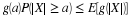, in that order, we may designate

(2.3)

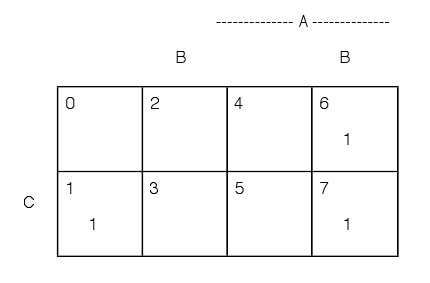
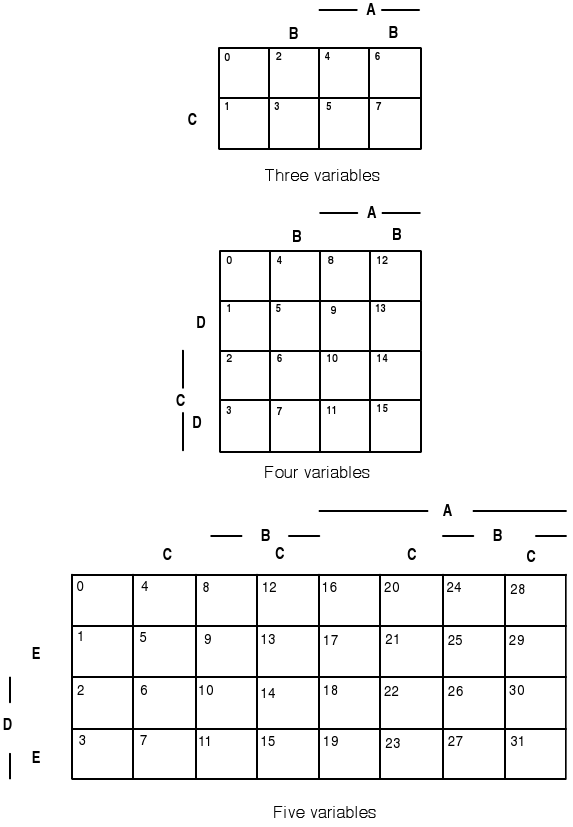
We utilize this numbering scheme on special Venn diagrams called minterm maps. These are illustrated in Figure 2.1, for the cases of three, four, and five generating events. Since the actual content of any minterm depends upon the sets 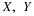, and D in the generating class, it is customary to refer to these sets as variables. In the three-variable case, set A is the right half of the diagram and set C is the lower half; but set B is split, so that it is the union of the second and fourth columns. Similar splits occur in the other cases.

Remark. Other useful arrangements of minterm maps are employed in the analysis of switching circuits.

Figure 2.1. 

Minterm maps for three, four, or five variables.

The significance of the minterm partition of the basic space rests in large measure on the following fact.

Minterm expansion

Each Boolean combination of the elements in a generating class may be expressed as the disjoint union of an appropriate subclass of the minterms. This representation is known as the minterm expansion for the combination.

In deriving an expression for a given Boolean combination which holds for any class 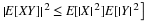of four events, we include all possible minterms, whether empty or not. If a minterm is empty for a given class, its presence does not modify the set content or probability assignment for the Boolean combination.

The existence and uniqueness of the expansion is made plausible by simple examples utilizing minterm maps to determine graphically the minterm content of various Boolean combinations. Using the arrangement and numbering system introduced above, we let M_i represent the ith minterm (numbering from zero) and let p(i) represent the probability of that minterm. When we deal with a union of minterms in a minterm expansion, it is convenient to utilize the shorthand illustrated in the following.

(2.4)

Figure 2.2. 

Minterm expansion for Example 2.1

Consider the following simple example.

A key to establishing the expansion is to note that each minterm is either a subset of the combination or is disjoint from it. The expansion is thus the union of those minterms included in the combination. A general verification using indicator functions is sketched in the last section of this module.

A typical problem seeks the probability of certain Boolean combinations of a class of events when the probabilities of various other combinations is given. We consider several simple examples and illustrate the use of minterm maps in formulation and solution.