TEASER - 01
BEAUTY CONTEST
Imagine a contest of beauty pageant. Participants come onto stage one by one in front of Judges for each event. The participants and Judges do not know each other. The Judges are asked to award points on a scale from 1 to 10 (no fractions) to each candidate.
If you are made one of the judge and is asked to choose one out of following choices for the first participant in first event which one would you choose ?


THE EXPLANATION:
The contests are generally conducted to select a winner from among a group of contestants. In a contest, it is not important how much marks or points (absolute) an individual gets, rather the whole process is to make a proper sorting from among a chaotic group through a comparative analysis. Sorting cannot be done in isolation, it can only be done if there are more than one candidates put together and compared together. If the winner candidate gets 5 point on a scale of 1 to 10, it does not mean that she or he is not worth 10, it merely indicates that all other candidates have points less than 5.
When 1st candidate comes onto stage, judges may find it difficult to award a point as they would not know whether she is best or worst among all candidates. Judges would normally rely on their own past experience to make an imaginary benchmark or standard and attempt a comparison with that. Therefore the whole process would be highly influenced by an individual’s experience which would amount to biased judgment, especially during initial stage.
If 1st candidate is awarded 1 point, for example, it would mean that an assumption has been made that all remaining candidates are better than her and would get either one or more than 1 point. Now if all remaining participants turn out to be worst than 1st candidate then there would be a big dilemma as no numbers are available less than one hence all shall end up having 1 point each. Similarly if 1st candidate is given 10 points same situation would arise in reverse order
Let us compare beauty contest (crude comparison) to a “ball game” where participants are replaced by balls of various sizes chaotically placed in a cluster. These balls are required to be sorted out based on their sizes.

CHAOTIC CLUSTER OF BALLS OF DIFFERENT SIZES
The balls are ten in numbers and named as A, B, C, D, E, F, G, H, J & K and judges award points on the basis of their sizes on a scale of 1 to 10 (no fractions). The smallest one gets 1 and largest one gets 10 points. The sizes of balls are not known to judges prior to contest.
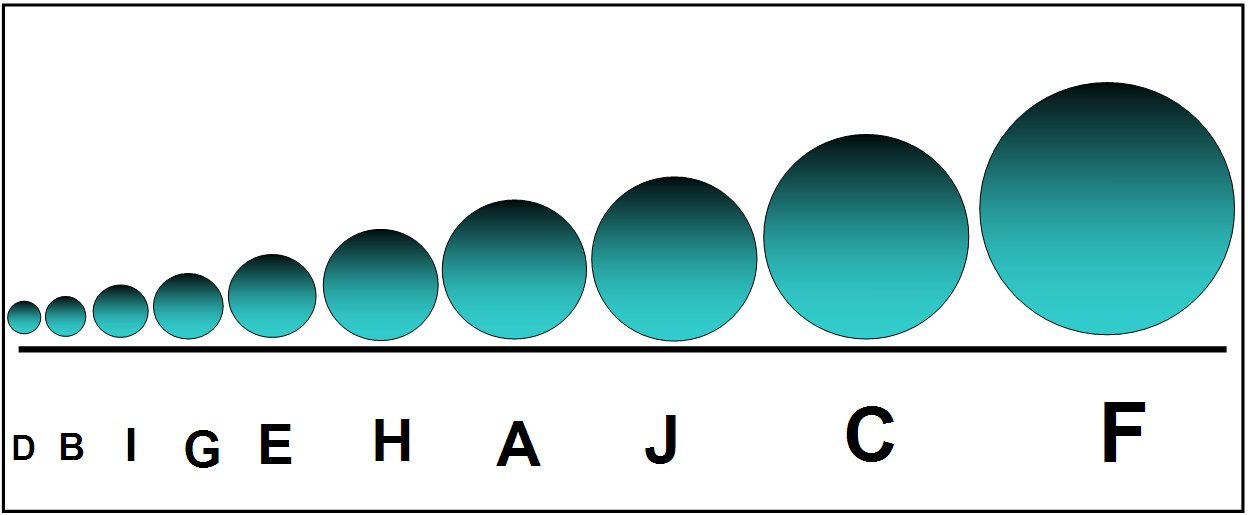
BALLS SORTED AS PER SIZES
The name and diameter of balls are shown in a table below:
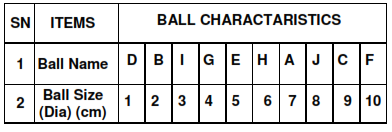
Let us imagine that D is the first one paraded in front of judges.
• If D is awarded 1 or 2 (minimum marks), the result would be correct up to 99%.
• However, if D is awarded 10 or 9 marks (maximum) the result will be 99% wrong.
• In case D is awarded 5 marks (mid point of scale), at least half of the remaining candidates would get correct markings.
• Suppose E is the first candidate paraded in front of judges and is awarded 1 or 2 marks (minimum), the result of contest would be 50% correct and if awarded 10 or 9 marks (maximum) still result would be 50% correct, however, if E gets 5 point (middle), the result would be 100% correct.
Awarding of marks at extreme end is a total gamble and there is every danger of going wrong by 99% and candidates may end up getting incorrect marks.
To be on safe side the correct way would be to choose the mid- point, i.e.5 so that a fair amount of points are available on either side and a dead end is avoided.
Following conclusion can be drawn from the analysis;
(a) If points are picked up from extreme ends of a scale (1, 2 or 9, 10) there is a danger of going 100% wrong or right by 0%. So the probability of choosing points correctly would always vary from 0% to 100%.
(b) However, if points are chosen from middle of the scale (5) the answer would always be 50% to 100% right and will never be 100% wrong. The probability of choosing points correctly would always vary from 50% to 100% and will never be less than 50%.
(c) Therefore the correct way would be to choose the mid-point for initial participants so that the danger of going wrong by 100% is avoided and a fair amount of points are made available on either side for awarding later participants and a dead end is averted.
********








