The Behaviour of Measuring-Rods and Clocks in Motion
Place a metre-rod in the x1-axis of K1 in such a manner that one end (the beginning) coincides with the point x1=0 whilst the other end (the end of the rod) coincides with the point x1=I. What is the length of the metre-rod relatively to the systemK? In order to learn this, we need only ask where the beginning of the rod and the end of the rod lie with respect to K at a particular time t of the system K. By means of the first equation of the Lorentz transformation the values of these two points at the timet = 0 can be shown to
be the distance between the points being .
But the metre-rod is moving with the velocity
v relative to
K. It therefore follows that the length of a rigid metre-rod moving in the direction of its length with a velocity
v is of a metre.
The rigid rod is thus shorter when in motion than when at rest, and the more quickly it is moving, the shorter is the rod. For the velocity
v=c we should have ,
and for still greater velocities the square-root becomes imaginary. From this we conclude that in the theory of relativity the velocity c plays the part of a limiting velocity, which can neither be reached nor exceeded by any real body.
Of course this feature of the velocity c as a limiting velocity also clearly follows from the equations of the Lorentz transformation, for these became meaningless if we choose values of v greater than c.
If, on the contrary, we had considered a metre-rod at rest in the x-axis with respect toK, then we should have found that the length of the rod as judged from K1 would have been; this is quite in accordance with the principle of relativity which forms the basis of our considerations.
A Priori it is quite clear that we must be able to learn something about the physical behaviour of measuring-rods and clocks from the equations of transformation, for the magnitudes z, y, x, t, are nothing more nor less than the results of measurements obtainable by means of measuring-rods and clocks. If we had based our considerations on the Galileian transformation we should not have obtained a contraction of the rod as a consequence of its motion.
Let us now consider a seconds-clock which is permanently situated at the origin ( x1=0) of K1. t1=0 and t1=I are two successive ticks of this clock. The first and fourth equations of the Lorentz transformation give for these two ticks :
t = 0
and As judged from K, the clock is moving with the velocity v; as judged from this reference-body, the time which elapses between two strokes of the clock is not one second, but seconds, i.e. a somewhat larger time. As a consequence of its motion the clock goes more slowly than when at rest. Here also the velocity c plays the part of an unattainable limiting velocity.
Theorem of the Addition ofNow in practice we can move clocks and measuring-rods only with velocities that are small compared with the velocity of light; hence we shall hardly be able to compare the results of the previous section directly with the reality. But, on the other hand, these results must strike you as being very singular, and for that reason I shall now draw another conclusion from the theory, one which can easily be derived from the foregoing considerations, and which has been most elegantly confirmed by experiment.
In Section 6 we derived the theorem of the addition of velocities in one direction in the form which also results from the hypotheses of classical mechanics- This theorem can also be deduced readily horn the Galilei transformation (Section 11). In place of the man walking inside the carriage, we introduce a point moving relatively to the co-ordinate systemK1 in accordance with the equation
1 = wt1x
By means of the first and fourth equations of the Galilei transformation we can express
x1 and
t1 in terms of
x and
t, and we then obtain
x = (v + w)t
This equation expresses nothing else than the law of motion of the point with reference to the systemK (of the man with reference to the embankment). We denote this velocity by the symbol W, and we then obtain, as in Section 6,
W=v+w A)
But we can carry out this consideration just as well on the basis of the theory of relativity. In the equation
x1 = wt1 B)
we must then express x1and t1 in terms ofx and t, making use of the first and fourth equations of the Lorentz transformation. Instead of the equation (A) we then obtain the equation

which corresponds to the theorem of addition for velocities in one direction according to the theory of relativity. The question now arises as to which of these two theorems is the better in accord with experience. On this point we axe enlightened by a most important experiment which the brilliant physicist Fizeau performed more than half a century ago, and which has been repeated since then by some of the best experimental physicists, so that there can be no doubt about its result. The experiment is concerned with the following question. Light travels in a motionless liquid with a particular velocity w. How quickly does it travel in the direction of the arrow in the tube T (see the accompanying diagram, Fig. 3) when the liquid above mentioned is flowing through the tube with a velocity v ?
In accordance with the principle of relativity we shall certainly have to take for granted that the propagation of light always takes place with the same velocity w with respect to the liquid, whether the latter is in motion with reference to other bodies or not. The velocity of light relative to the liquid and the velocity of the latter relative to the tube are thus known, and we require the velocity of light relative to the tube.
It is clear that we have the problem of Section 6 again before us. The tube plays the part of the railway embankment or of the co-ordinate systemK, the liquid plays the part of the carriage or of the co-ordinate systemK1, and finally, the light plays the part of the
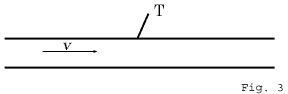
man walking along the carriage, or of the moving point in the present section. If we denote the velocity of the light relative to the tube by W, then this is given by the equation (A) or (B), according as the Galilei transformation or the Lorentz transformation corresponds to the facts. Experiment1) decides in favour of equation (B) derived from the theory of relativity, and the agreement is, indeed, very exact. According to recent and most excellent measurements by Zeeman, the influence of the velocity of flow v on the propagation of light is represented by formula (B) to within one per cent.
Nevertheless we must now draw attention to the fact that a theory of this phenomenon was given by H. A. Lorentz long before the statement of the theory of relativity. This theory was of a purely electrodynamical nature, and was obtained by the use of particular hypotheses as to the electromagnetic structure of matter. This circumstance, however, does not in the least diminish the conclusiveness of the experiment as a crucial test in favour of the theory of relativity, for the electrodynamics of Maxwell-Lorentz, on which the original theory was based, in no way opposes the theory of relativity. Rather has the latter been developed from electrodynamics as an astoundingly simple combination and generalisation of the hypotheses, formerly independent of each other, on which electrodynamics was built.
Footnotes
1) Fizeau found
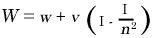
, where
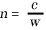
is the index of refraction of the liquid. On the other hand, owing to the smallness of
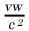
as compared with
I,
we can replace (B) in the first place by
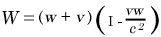
, or to the same order of approximation by
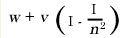
, which agrees with Fizeau's result.






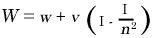 , where
, where 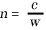 is the index of refraction of the liquid. On the other hand, owing to the smallness of
is the index of refraction of the liquid. On the other hand, owing to the smallness of 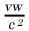 as compared with
as compared with 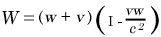 , or to the same order of approximation by
, or to the same order of approximation by 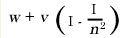 , which agrees with Fizeau's result.
, which agrees with Fizeau's result.