Minkowski's Four−Dimensional Space ("World") (supplementary to section 17)
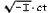
in place of t, as time−variable. If, in accordance with this, we insert
x1 = x
x2 = y
x3 = z
x4 =
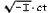
and similarly for the accented system K
1, then the condition which is identically satisfied by the transformation can be expressed thus :
x
1'
2 + x
2'
2 + x
3'
2 + x
4'
2 = x
12 + x
22 + x
32 + x
42 (12).
That is, by the afore−mentioned choice of " coordinates," (11a) [see the end of
Appendix II] is transformed into this equation.
We see from (12) that the imaginary time co−ordinate x4, enters into the condition of transformation in exactly the same way as the space co−ordinates x1, x2, x3. It is due to this fact that, according to the theory of relativity, the " time "x4, enters into natural laws in the same form as the space co ordinates x1, x2, x3.
A four−dimensional continuum described by the "co−ordinates" x1, x2, x3, x4, was called "world" by Minkowski, who also termed a point−event a " world−point." From a "happening" in three−dimensional space, physics becomes, as it were, an " existence " in the four−dimensional " world."
This four−dimensional " world " bears a close similarity to the three−dimensional " space " of (Euclidean) analytical geometry. If we introduce into the latter a new Cartesian co−ordinate system (x'1, x'2, x'3) with the same origin, then x'1, x'2, x'3, are linear homogeneous functions of x1, x2, x3 which identically satisfy the equation
x'
12 + x'
22 + x'
32 = x
12 + x
22 + x
32
The analogy with (12) is a complete one. We can regard Minkowski's " world " in a formal manner as a four−dimensional Euclidean space (with an imaginary time coordinate) ; the Lorentz transformation corresponds to a " rotation " of the co−ordinate system in the fourdimensional " world."
Next:
The Experimental Confirmation of the General Theory of Relativity Relativity: The Special and General Theory Appendix
Appendix III




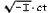 in place of t, as time−variable. If, in accordance with this, we insert
in place of t, as time−variable. If, in accordance with this, we insert