The basal principle, which was the pivot of all our previous considerations, was the special principle of relativity, i.e. the principle of the physical relativity of all uniform motion. Let as once more analyse its meaning carefully.
It was at all times clear that, from the point of view of the idea it conveys to us, every motion must be considered only as a relative motion. Returning to the illustration we have frequently used of the embankment and the railway carriage, we can express the fact of the motion here taking place in the following two forms, both of which are equally justifiable :
(a) The carriage is in motion relative to the embankment, (b) The embankment is in motion relative to the carriage.In (a) the embankment, in (b) the carriage, serves as the body of reference in our statement of the motion taking place. If it is simply a question of detecting or of describing the motion involved, it is in principle immaterial to what reference−body we refer the motion. As already mentioned, this is self−evident, but it must not be confused with the much more comprehensive statement called "the principle of relativity," which we have taken as the basis of our investigations.
The principle we have made use of not only maintains that we may equally well choose the carriage or the embankment as our reference−body for the description of any event (for this, too, is self−evident). Our principle rather asserts what follows : If we formulate the general laws of nature as they are obtained from experience, by making use of
(a) the embankment as reference−body, (b) the railway carriage as reference−body,then these general laws of nature ( e.g. the laws of mechanics or the law of the propagation of light in vacuo) have exactly the same form in both cases. This can also be expressed as follows : For the physical description of natural processes, neither of the reference bodies K, K1 is unique (lit. " specially marked out ") as compared with the other. Unlike the first, this latter statement need not of necessity hold a priori; it is not contained in the conceptions of " motion" and " reference−body " and derivable from them; only experience can decide as to its correctness or incorrectness.
Up to the present, however, we have by no means maintained the equivalence of all bodies of reference K in connection with the formulation of natural laws. Our course was more on the following Iines. In the first place, we started out from the assumption that there exists a reference−body K, whose condition of motion is such that the Galileian law holds with respect to it : A particle left to itself and sufficiently far removed from all other particles moves uniformly in a straight line. With reference to K (Galileian reference−body) the laws of nature were to be as simple as possible. But in addition to K, all bodies of reference K1 should be given preference in this sense, and they should be exactly equivalent to K for the formulation of natural laws, provided that they are in a state of uniform rectilinear and non−rotary motion with respect to K ; all these bodies of reference are to be regarded as Galileian reference−bodies. The validity of the principle of relativity was assumed only for these reference−bodies, but not for others (e.g. those possessing motion of a different kind). In this sense we speak of the special principle of relativity, or special theory of relativity.
In contrast to this we wish to understand by the "general principle of relativity" the following statement : All bodies of reference K, K1, etc., are equivalent for the description of natural phenomena (formulation of the general laws of nature), whatever may be their state of motion. But before proceeding farther, it ought to be pointed out that this formulation must be replaced later by a more abstract one, for reasons which will become evident at a later stage.
Since the introduction of the special principle of relativity has been justified, every intellect which strives after generalisation must feel the temptation to venture the step towards the general principle of relativity. But a simple and apparently quite reliable consideration seems to suggest that, for the present at any rate, there is little hope of success in such an attempt; Let us imagine ourselves transferred to our old friend the railway carriage, which is travelling at a uniform rate. As long as it is moving unifromly, the occupant of the carriage is not sensible of its motion, and it is for this reason that he can without reluctance interpret the facts of the case as indicating that the carriage is at rest, but the embankment in motion. Moreover, according to the special principle of relativity, this interpretation is quite justified also from a physical point of view.
If the motion of the carriage is now changed into a non−uniform motion, as for instance by a powerful application of the brakes, then the occupant of the carriage experiences a correspondingly powerful jerk forwards. The retarded motion is manifested in the mechanical behaviour of bodies relative to the person in the railway carriage. The mechanical behaviour is different from that of the case previously considered, and for this reason it would appear to be impossible that the same mechanical laws hold relatively to the non−uniformly moving carriage, as hold with reference to the carriage when at rest or in uniform motion. At all events it is clear that the Galileian law does not hold with respect to the non−uniformly moving carriage. Because of this, we feel compelled at the present juncture to grant a kind of absolute physical reality to non−uniform motion, in opposition to the general principle of relatvity. But in what follows we shall soon see that this conclusion cannot be maintained.
Next: The Gravitational Field Part II: The General Theory of Relativity"If we pick up a stone and then let it go, why does it fall to the ground ?" The usual answer to this question is: "Because it is attracted by the earth." Modern physics formulates the answer rather differently for the following reason. As a result of the more careful study of electromagnetic phenomena, we have come to regard action at a distance as a process impossible without the intervention of some intermediary medium. If, for instance, a magnet attracts a piece of iron, we cannot be content to regard this as meaning that the magnet acts directly on the iron through the intermediate empty space, but we are constrained to imagine — after the manner of Faraday — that the magnet always calls into being something physically real in the space around it, that something being what we call a "magnetic field." In its turn this magnetic field operates on the piece of iron, so that the latter strives to move towards the magnet. We shall not discuss here the justification for this incidental conception, which is indeed a somewhat arbitrary one. We shall only mention that with its aid electromagnetic phenomena can be theoretically represented much more satisfactorily than without it, and this applies particularly to the transmission of electromagnetic waves. The effects of gravitation also are regarded in an analogous manner.
The action of the earth on the stone takes place indirectly. The earth produces in its surrounding a gravitational field, which acts on the stone and produces its motion of fall. As we know from experience, the intensity of the action on a body dimishes according to a quite definite law, as we proceed farther and farther away from the earth. From our point of view this means : The law governing the properties of the gravitational field in space must be a perfectly definite one, in order correctly to represent the diminution of gravitational action with the distance from operative bodies. It is something like this: The body (e.g. the earth) produces a field in its immediate neighbourhood directly; the intensity and direction of the field at points farther removed from the body are thence determined by the law which governs the properties in space of the gravitational fields themselves.
In contrast to electric and magnetic fields, the gravitational field exhibits a most remarkable property, which is of fundamental importance for what follows. Bodies which are moving under the sole influence of a gravitational field receive an acceleration, which does not in the least depend either on the material or on the physical state of the body. For instance, a piece of lead and a piece of wood fall in exactly the same manner in a gravitational field (in vacuo), when they start off from rest or with the same initial velocity. This law, which holds most accurately, can be expressed in a different form in the light of the following consideration.
According to Newton's law of motion, we have(Force) = (inertial mass) x (acceleration),
where the "inertial mass" is a characteristic constant of the accelerated body. If now gravitation is the cause of the acceleration, we then have
(Force) = (gravitational mass) x (intensity of the gravitational field),
where the "gravitational mass" is likewise a characteristic constant for the body. From these two relations follows:
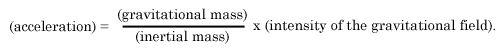
If now, as we find from experience, the acceleration is to be independent of the nature and the condition of the body and always the same for a given gravitational field, then the ratio of the gravitational to the inertial mass must likewise be the same for all bodies. By a suitable choice of units we can thus make this ratio equal to unity. We then have the following law: The gravitational mass of a body is equal to its inertial maw.
It is true that this important law had hitherto been recorded in mechanics, but it had not been interpreted. A satisfactory interpretation can be obtained only if we recognise the following fact : The same quality of a body manifests itself according to circumstances as " inertia " or as " weight " (lit. " heaviness '). In the following section we shall show to what extent this is actually the case, and how this question is connected with the general postulate of relativity.
Next: The Equality of Inertial and Gravitational Mass as an argument for the General Postule of RelativityWe imagine a large portion of empty space, so far removed from stars and other appreciable masses, that we have before us approximately the conditions required by the fundamental law of Galilei. It is then possible to choose a Galileian reference−body for this part of space (world), relative to which points at rest remain at rest and points in motion continue permanently in uniform rectilinear motion. As reference−body let us imagine a spacious chest resembling a room with an observer inside who is equipped with apparatus. Gravitation naturally does not exist for this observer. He must fasten himself with strings to the floor, otherwise the slightest impact against the floor will cause him to rise slowly towards the ceiling of the room.
To the middle of the lid of the chest is fixed externally a hook with rope attached, and now a " being " (what kind of a being is immaterial to us) begins pulling at this with a constant force. The chest together with the observer then begin to move "upwards" with a uniformly accelerated motion. In course of time their velocity will reach unheard−of values — provided that we are viewing all this from another reference−body which is not being pulled with a rope.
But how does the man in the chest regard the Process ? The acceleration of the chest will be transmitted to him by the reaction of the floor of the chest. He must therefore take up this pressure by means of his legs if he does not wish to be laid out full length on the floor. He is then standing in the chest in exactly the same way as anyone stands in a room of a home on our earth. If he releases a body which he previously had in his land, the accelertion of the chest will no longer be transmitted to this body, and for this reason the body will approach the floor of the chest with an accelerated relative motion. The observer will further convince himself that the acceleration of the body towards the floor of the chest is always of the same magnitude, whatever kind of body he may happen to use for the experiment.
Relying on his knowledge of the gravitational field (as it was discussed in the preceding section), the man in the chest will thus come to the conclusion that he and the chest are in a gravitational field which is constant with regard to time. Of course he will be puzzled for a moment as to why the chest does not fall in this gravitational field. just then, however, he discovers the hook in the middle of the lid of the chest and the rope which is attached to it, and he consequently comes to the conclusion that the chest is suspended at rest in the gravitational field.
Ought we to smile at the man and say that he errs in his conclusion ? I do not believe we ought to if we wish to remain consistent ; we must rather admit that his mode of grasping the situation violates neither reason nor known mechanical laws. Even though it is being accelerated with respect to the "Galileian space" first considered, we can nevertheless regard the chest as being at rest. We have thus good grounds for extending the principle of relativity to include bodies of reference which are accelerated with respect to each other, and as a result we have gained a powerful argument for a generalised postulate of relativity.
We must note carefully that the possibility of this mode of interpretation rests on the fundamental property of the gravitational field of giving all bodies the same acceleration, or, what comes to the same thing, on the law of the equality of inertial and gravitational mass. If this natural law did not exist, the man in the accelerated chest would not be able to interpret the behaviour of the bodies around him on the supposition of a gravitational field, and he would not be justified on the grounds of experience in supposing his reference−body to be " at rest."
Suppose that the man in the chest fixes a rope to the inner side of the lid, and that he attaches a body to the free end of the rope. The result of this will be to strech the rope so that it will hang " vertically " downwards. If we ask for an opinion of the cause of tension in the rope, the man in the chest will say: "The suspended body experiences a downward force in the gravitational field, and this is neutralised by the tension of the rope ; what determines the magnitude of the tension of the rope is the gravitational mass of the suspended body." On the other hand, an observer who is poised freely in space will interpret the condition of things thus : " The rope must perforce take part in the accelerated motion of the chest, and it transmits this motion to the body attached to it. The tension of the rope is just large enough to effect the acceleration of the body. That which determines the magnitude of the tension of the rope is the inertial mass of the body." Guided by this example, we see that our extension of the principle of relativity implies the necessity of the law of the equality of inertial and gravitational mass. Thus we have obtained a physical interpretation of this law.
From our consideration of the accelerated chest we see that a general theory of relativity must yield important results on the laws of gravitation. In point of fact, the systematic pursuit of the general idea of relativity has supplied the laws satisfied by the gravitational field. Before proceeding farther, however, I must warn the reader against a misconception suggested by these considerations. A gravitational field exists for the man in the chest, despite the fact that there was no such field for the co−ordinate system first chosen. Now we might easily suppose that the existence of a gravitational field is always only an apparent one. We might also think that, regardless of the kind of gravitational field which may be present, we could always choose another reference−body such that no gravitational field exists with reference to it. This is by no means true for all gravitational fields, but only for those of quite special form. It is, for instance, impossible to choose a body of reference such that, as judged from it, the gravitational field of the earth (in its entirety) vanishes.
We can now appreciate why that argument is not convincing, which we brought forward against the general principle of relativity at theend of Section 18. It is certainly true that the observer in the railway carriage experiences a jerk forwards as a result of the application of the brake, and that he recognises, in this the non−uniformity of motion (retardation) of the carriage. But he is compelled by nobody to refer this jerk to a " real " acceleration (retardation) of the carriage. He might also interpret his experience thus: " My body of reference (the carriage) remains permanently at rest. With reference to it, however, there exists (during the period of application of the brakes) a gravitational field which is directed forwards and which is variable with respect to time. Under the influence of this field, the embankment together with the earth moves non−uniformly in such a manner that their original velocity in the backwards direction is continuously reduced."
Next: In What Respects are the Foundations of Classical Mechanics and of the Special Theory of Relativity Unsatisfactory?We have already stated several times that classical mechanics starts out from the following law: Material particles sufficiently far removed from other material particles continue to move uniformly in a straight line or continue in a state of rest. We have also repeatedly emphasised that this fundamental law can only be valid for bodies of reference K which possess certain unique states of motion, and which are in uniform translational motion relative to each other. Relative to other reference−bodies K the law is not valid. Both in classical mechanics and in the special theory of relativity we therefore differentiate between reference−bodies K relative to which the recognised " laws of nature " can be said to hold, and reference−bodies K relative to which these laws do not hold.
But no person whose mode of thought is logical can rest satisfied with this condition of things. He asks : " How does it come that certain reference−bodies (or their states of motion) are given priority over other reference−bodies (or their states of motion) ? What is the reason for this Preference? In order to show clearly what I mean by this question, I shall make use of a comparison.
I am standing in front of a gas range. Standing alongside of each other on the range are two pans so much alike that one may be mistaken for the other. Both are half full of water. I notice that steam is being emitted continuously from the one pan, but not from the other. I am surprised at this, even if I have never seen either a gas range or a pan before. But if I now notice a luminous something of bluish colour under the first pan but not under the other, I cease to be astonished, even if I have never before seen a gas flame. For I can only say that this bluish something will cause the emission of the steam, or at least possibly it may do so. If, however, I notice the bluish something in neither case, and if I observe that the one continuously emits steam whilst the other does not, then I shall remain astonished and dissatisfied until I have discovered some circumstance to which I can attribute the different behaviour of the two pans.
Analogously, I seek in vain for a real something in classical mechanics (or in the special theory of relativity) to which I can attribute the different behaviour of bodies considered with respect to the reference systems K and K1.1) Newton saw this objection and attempted to invalidate it, but without success. But E. Mach recognsed it most clearly of all, and because of this objection he claimed that mechanics must be placed on a new basis. It can only be got rid of by means of a physics which is conformable to the general principle of relativity, since the equations of such a theory hold for every body of reference, whatever may be its state of motion.
Next: A Few Inferences from the General Principle of RelativityFootnotes
1) The objection is of importance more especially when the state of motion of the reference−body is of such a nature that it does not require any external agency for its maintenance, e.g. in the case when the reference−body is rotating uniformly.
Relativity: The Special and General Theory Part II: The General Theory of RelativityThe considerations of Section 20 show that the general principle of relativity puts us in a position to derive properties of the gravitational field in a purely theoretical manner. Let us suppose, for instance, that we know the space−time " course " for any natural process whatsoever, as regards the manner in which it takes place in the Galileian domain relative to a Galileian body of reference K. By means of purely theoretical operations (i.e. simply by calculation) we are then able to find how this known natural process appears, as seen from a reference−body K1 which is accelerated relatively to K. But since a gravitational field exists with respect to this new body of reference K1, our consideration also teaches us how the gravitational field influences the process studied.
For example, we Wayrn that a body which is in a state of uniform rectilinear motion with respect to K (in accordance with the law of Galilei) is executing an accelerated and in general curvilinear motion with respect to the accelerated reference−body K1 (chest). This acceleration or curvature corresponds to the influence on the moving body of the gravitational field prevailing relatively to K. It is known that a gravitational field influences the movement of bodies in this way, so that our consideration supplies us with nothing essentially new.
However, we obtain a new result of fundamental importance when we carry out the analogous consideration for a ray of light. With respect to the Galileian reference−body K, such a ray of light is transmitted rectilinearly with the velocity c. It can easily be shown that the path of the same ray of light is no longer a straight line when we consider it with reference to the accelerated chest (reference−body K1). From this we conclude, that, in general, rays of light are propagated curvilinearly in gravitational fields. In two respects this result is of great importance.
In the first place, it can be compared with the reality. Although a detailed examination of the question shows that the curvature of light rays required by the genernal theory of relativity is only exceedingly small for the gravitational fields at our disposal in practice, its estimated magnitude for light rays passing the sun at grazing incidence is nevertheless 1.7 seconds of arc. This ought to manifest itself in the following way. As seen from the earth, certain fixed stars appear to be in the neighbourhood of the sun, and are thus capable of observation during a total eclipse of the sun. At such times, these stars ought to appear to be displaced outwards from the sun by an amount indicated above, as compared with their apparent position in the sky when the sun is situated at another part of the heavens. The examination of the correctness or otherwise of this deduction is a problem of the greatest importance, the early solution of which is to be expected of astronomers.1)
In the second place our result shows that, according to the general theory of relativity, the law of the constancy of the velocity of light in vacuo, which constitutes one of the two fundamental assumptions in the special theory of relativity and to which we have already frequently referred, cannot claim any unlimited validity. A curvature of rays of light can only take place when the velocity of propagation of light varies with position. Now we might think that as a consequence of this, the special theory of relativity and with it the whole theory of relativity would be laid in the dust. But in reality this is not the case. We can only conclude that the special theory of relativity cannot claim an unlinlited domain of validity ; its results hold only so long as we are able to disregard the influences of gravitational fields on the phenomena (e.g. of light).
Since it has often been contended by opponents of the theory of relativity that the special theory of relativity is overthrown by the general theory of relativity, it is perhaps advisable to make the facts of the case clearer by means of an appropriate comparison. Before the development of electrodynamics the laws of electrostatics were looked upon as the laws of electricity. At the present time we know that electric fields can be derived correctly from electrostatic considerations only for the case, which is never strictly realised, in which the electrical masses are quite at rest relatively to each other, and to the co−ordinate system. Should we be justified in saying that for this reason electrostatics is overthrown by the field−equations of Maxwell in electrodynamics ? Not in the least. Electrostatics is contained in electrodynamics as a limiting case ; the laws of the latter lead directly to those of the former for the case in which the fields are invariable with regard to time. No fairer destiny could be allotted to any physical theory, than that it should of itself point out the way to the introduction of a more comprehensive theory, in which it lives on as a limiting case.
In the example of the transmission of light just dealt with, we have seen that the general theory of relativity enables us to derive theoretically the influence of a gravitational field on the course of natural processes, the Iaws of which are already known when a gravitational field is absent. But the most attractive problem, to the solution of which the general theory of relativity supplies the key, concerns the investigation of the laws satisfied by the gravitational field itself. Let us consider this for a moment.
We are acquainted with space−time domains which behave (approximately) in a " Galileian " fashion under suitable choice of reference−body, i.e. domains in which gravitational fields are absent. If we now refer such a domain to a reference−body K1 possessing any kind of motion, then relative to K1 there exists a gravitational field which is variable with respect to space and time.2) The character of this field will of course depend on the motion chosen for K1. According to the general theory of relativity, the general law of the gravitational field must be satisfied for all gravitational fields obtainable in this way. Even though by no means all gravitationial fields can be produced in this way, yet we may entertain the hope that the general law of gravitation will be derivable from such gravitational fields of a special kind. This hope has been realised in the most beautiful manner. But between the clear vision of this goal and its actual realisation it was necessary to surmount a serious difficulty, and as this lies deep at the root of things, I dare not withhold it from the reader. We require to extend our ideas of the space−time continuum still farther.
Next: Behaviour of Clocks and Measuring−Rods on a Rotating Body of ReferenceFootnotes
1) By means of the star photographs of two expeditions equipped by a Joint Committee of the Royal and Royal Astronomical Societies, the existence of the deflection of light demanded by theory was first confirmed during the solar eclipse of 29th May, 1919. (Cf. Appendix III.)
2) This follows from a generalisation of the discussion in Section 20 Part II: The General Theory of RelativityHitherto I have purposely refrained from speaking about the physical interpretation of space− and time−data in the case of the general theory of relativity. As a consequence, I am guilty of a certain slovenliness of treatment, which, as we know from the special theory of relativity, is far from being unimportant and pardonable. It is now high time that we remedy this defect; but I would mention at the outset, that this matter lays no small claims on the patience and on the power of abstraction of the reader.
We start off again from quite special cases, which we have frequently used before. Let us consider a space time domain in which no gravitational field